ブラウザの印刷機能を使って印刷またはPDF変換してください.
用紙サイズはA4のみ対応しています.
離散最適化とその応用

神山 直之
学位:博士(工学)(京都大学)
専門分野:離散最適化,グラフ理論,計算量理論
私の専門分野は離散最適化の理論的研究です.加えて,離散最適化と関係の深いグラフ理論や計算量理論の研究も行っています.これらの分野は数学と計算機科学の落ち合うところに位置し,互いに深く絡み合っています.これらの分野が含む問題は非常に多岐に渡るのですが,私は離散的な凸性である劣モジュラ性や,双対性を基本とする多面体的手法などを通じて,統一的な理解を深めることを目標としています.以下では,私が興味を持っている問題と併せて,これらの分野の簡単な説明をさせていただきます.
付記されている数字は相手に対する選好順序.(右)割り当ての例.
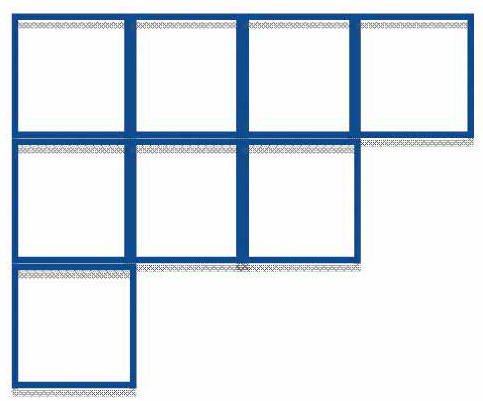
まず離散最適化ですが,そもそも最適化とは幾つかの解の候補から,目的関数を最大化もしくは最小化する解を求める問題です.離散最適化の研究においては,その中でも解の候補が離散的(つまりばらばら)な性質を持つ問題を扱います.これらの問題に対して,解の集合がどのような性質を満たすならば,全ての解の候補を調べずに効率的に最適解を見つけることができるかを明らかにし,実際にその解を求める方法(アルゴリズムと呼ばれます)を構築することが大きな目標となります.この分野に対して,私は二つの集合間の良い割り当てを求める安定マッチング問題や(図1参照),ものの流れを数理モデル化したネットワークフロー,そして離散最適化における抽象的な枠組みである劣モジュラ関数やマトロイドに関係する最適化問題などの研究を行っています.
続いては,グラフ理論です.グラフとは点とそれらをつなぐ辺で構成されるもので,幾何学的な位置関係ではなく,位相的にどのように接続しているかのみに注目したものです(図2参照).直観的には,道路等のネットワークを数学的に表わしたものだと思っていただければよいでしょう.そして,グラフ理論とは様々なグラフの持つ特性を一般的に明らかにする学問です.例えば,どのようなグラフならば高い頑健性を持っているかを考えたりします.このグラフ理論においては,私は古典的な問題である有向木の詰込問題における最大最小定理や(図2参照),グラフ上の最適化問題である辺支配集合問題などの研究を行っています.
最後に計算量理論です.上記の二つの分野がどちらかといえば「できる」ことを研究する学問だったのに対し,この分野は「できない」ことを研究する分野です.具体的には,計算機における「計算」を数学的に定義しその能力の限界を研究するものです.この分野においては,クレイ数学研究所の発表したミレニアム懸賞問題の一つである「P対NP問題」が象徴的な問題だといえるでしょう.一見,最適化と計算量理論の分野は相反するものに見えますが,実はそうではなく近年計算量理論の研究においても最適化の手法が使用されるようになってきています.私はこの計算量理論の研究において,離散最適化の分野で用いられている手法,例えば多面体的アプローチ等をどのように活用することができるかを明らかにすることに興味があります.
また,これらの分野の研究は,現実社会の問題を数理モデル化し解決するオペレーションズ・リサーチと呼ばれる分野と非常に相性が非常に良く,私自身も交通や都市計画,そしてソーシャルネットワーク等の現実的な問題から生じる問題に対して得られた理論的成果を応用することに興味があります.
Modeling, Analysis, Optimization, and Control of Complex and Networked Systems

Hoa Dinh NGUYEN
学位:PhD (Information Science and Technology), (The University of Tokyo).
専門分野:Modeling, optimization and control toward low-carbon and autonomous energy, transportation and other interconnected, complex systems. Particular focuses are on renewables and distributed energy resources, smart grid, intelligent transportation, multi-agent systems, graph theory, artificial intelligence, and decentralized optimization.
My research theme is Modeling, Analysis, Optimization, and Control of Complex and Networked Systems. The research goal is theoretical approaches for the modelling, exploration, analysis, and optimal, robust and resilient decision-making for complex and networked systems. To achieve that, a variety of mathematical framework will be employed, for example, dynamical systems and their stability theories, linear and nonlinear optimization, graph theory, control theory, differential geometry, bifurcation theory, and artificial intelligence.
Particular application areas include smart grid, smart cities, renewable and distributed energy systems, cyber-physical systems, wireless power transfer, intelligent and decarbonized transportation systems, bio systems for clean energy production and carbon capture. An illustration for smart grids, an example of such complex systems, is depicted in Fig. 1.
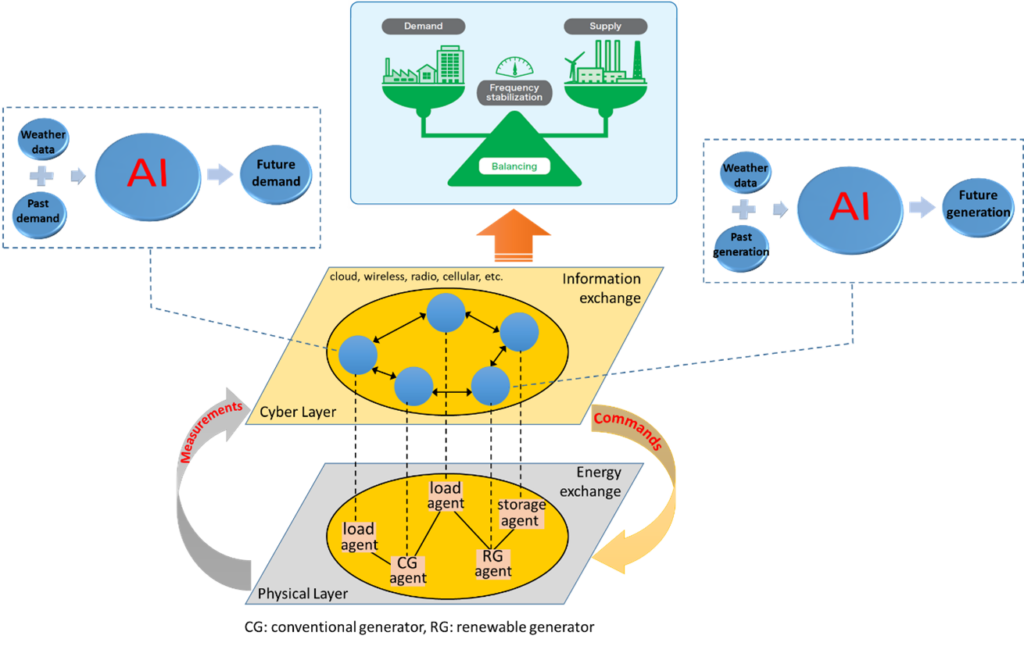
Figure 1. Illustration for modeling, decision and control in smart grids.
調和解析的手法に基づく放物型偏微分方程式の数学解析

武内 太貴
学位:博士(理学)(早稲田大学)
専門分野:放物型偏微分方程式論、調和解析学
私は放物型偏微分方程式を中心に研究しています。ここでいう「放物型」ですが、これは偏微分方程式の分類の1つで、最も基本的な放物型偏微分方程式として熱方程式が挙げられます。

例えばフライパンをコンロで加熱した際、フライパンの温度の推移は熱方程式に従います。もちろん実世界の現象は多様な外的要因に依存しますのでそれほど単純ではありませんが、理想的な状況下では物理現象を微分方程式によって表現できます。この熱方程式は最も基本的な例ですが、他にも様々な物理現象を放物型偏微分方程式によって表現できます。例えば(水などの)非圧縮性粘性流体の運動方程式であるNavier–Stokes方程式系や、細胞が特定の化学物質に反応して凝集する現象(走化性現象)を表すKeller–Segel方程式系などです。
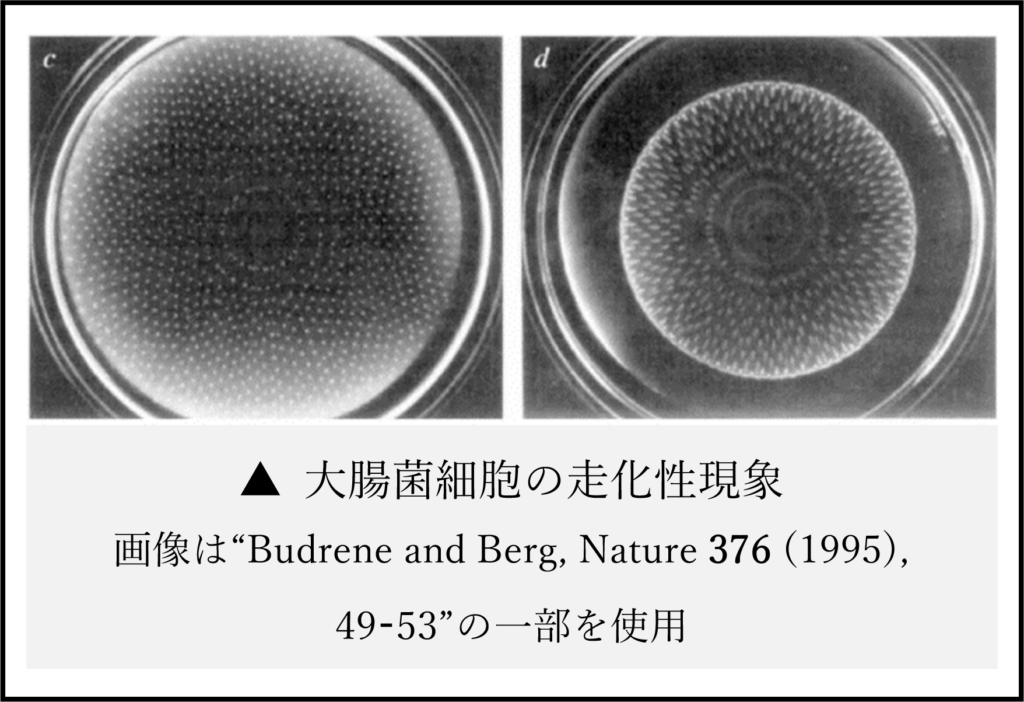
なおNavier–Stokes方程式系は流体力学の基礎であり、気象学や機械工学をはじめとした多くの実社会への応用分野を支えています。一方Keller–Segel方程式系はがん細胞の転移現象やアルツハイマー病の進行現象に応用され、こちらも医療技術において重要な位置付けにあります。このように、(放物型)偏微分方程式の数学解析は、種々の物理現象を解明して実社会へ役立てる基礎的な役割を果たしています。
それでは実際に放物型偏微分方程式をどのように解析するか考えてみましょう。微分方程式論における最も基本的な問いは、「解が存在するかどうか」です。微分方程式によって物理現象が表されていれば、理論的な解析はせずとも数値シミュレーションで現象を予測できます。しかし、本当にその微分方程式が物理現象を正しく表しているかは定かではなく、微分方程式に数学的な解が存在しない可能性があります。もしそうならば、存在しない解を数値シミュレーションで探すことになってしまいます。そのような事情から、まず解が存在することを理論的に裏付けたいということが数学的な動機付けの1つです。特に、私は解の存在が保証される数学的条件の枠組みをできるだけ広げたいという動機があります。
そこで次に述べたいキーワードが「調和解析」です。微分方程式の解析手法はいくつかありますが、私はその中でも調和解析的手法に基づいた研究を行っています。多くの方がどこかでFourier変換という言葉を聞いたことがあると思いますが、調和解析とはFourier変換を用いた解析のことです。

微分方程式の数学解析では関数空間の設定が必要不可欠ですが、調和解析に基づいた関数空間の導入は私の研究手法においては非常に強力な道具です。特に、関数の滑らかさを古典的な微分可能性という表現でなく、関数の持つ周波数に応じた増大度で表現できる点が有用で、線形解作用素や特異積分作用素などを容易に取り扱うことができるようになります。
(放物型)偏微分方程式を調和解析的手法に基づいて解析する研究はこれまでにも多く行われてきました。現在では様々なことが明らかになっている一方で、この方向性の研究にはさらなる発展も期待されています。私の研究もそれらの発展の一助になればよいと考えています。
離散微分幾何・可積分系

梶原 健司
学位:博士(工学)(東京大学)
専門分野:離散微分幾何,可積分系,パンルヴェ系,離散・超離散系
ソリトンと呼ばれる,粒子性をあわせ持つ非線形波動の研究に端を発する「可積分系」の研究を軸に研究活動を行っています.数理的には,ソリトンを記述する基礎方程式(ソリトン方程式)は非線形偏微分方程式であるにもかかわらず厳密に解けるという,奇跡的な性質を持っています.その奇跡の背後には「無限自由度の対称性をもつ無限次元の空間」の数理があり,その数理を共有する函数方程式の族を「可積分系」と呼びます.背後の数理を深く理解することによって,可積分系は多くの分野への応用が可能です.以下,私が関わっている3つの例を挙げます.
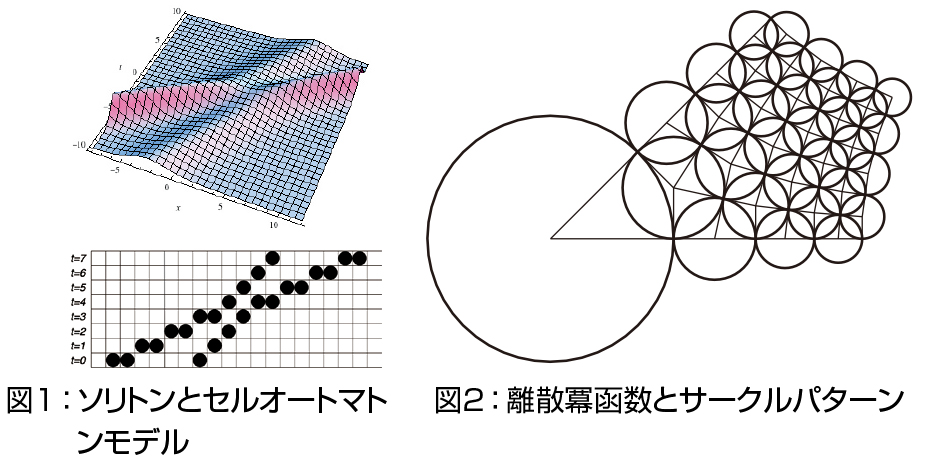
1. 離散化と超離散化:ソリトン方程式の可積分性を保存したまま独立変数を離散化して差分方程式を構成したり,従属変数まで離散化してセルオートマトンを構成する方法(「超離散化」)が構築されています.図1上は典型的なソリトンの相互作用を表し,左からやってきた大きく速いソリトンが小さく遅いソリトンを追い抜いています.一方,図1下はソリトンを記述するセルオートマトンです.1次元の箱の列と玉があるとし,各時刻で左から玉を右の最も近い空箱に移し,全ての玉を移動したら時刻を1進めます.この単純なモデルがソリトンを記述し,超離散化の手続きで偏微分方程式と直接の対応がつきます.離散化・超離散化の理論は数値解析や交通流など広範な分野に応用され,大きな成功を収めており,私が展開する他分野,特に幾何に関係する分野との連携活動のバックボーンを成しています(離散微分幾何).最近では超離散化の適用範囲が可積分ではない反応拡散系にも拡大され,性質のよい反応拡散セルオートマトンモデルが構成できるようになっています.さらに,超離散系の背後の構造が最近急速に発達している「トロピカル幾何学」でよく記述されることが判明し,純粋数学の発達も促しています.
2. 離散パンルヴェ方程式と楕円曲線:離散パンルヴェ方程式と呼ばれる可積分な2階常差分方程式の族は,数理物理学や特殊函数論で重要な役割を果たし,背後に極めて豊富な構造があります.その解はよく知られたベッセル函数や超幾何函数などの特殊函数の一般化と見なすことができます.これらの頂上にE8(1)型の対称性を持つ「楕円パンルヴェ方程式」があり,特殊解として楕円テータ函数で表示される「楕円超幾何函数」が現れます.この函数は超幾何型特殊函数の頂上に位置するものと考えられています. 離散微分幾何における応用の一つとして,ある種の複素正則函数の離散化をパンルヴェ・離散パンルヴェ方程式が記述します.図2は冪函数Z1/2の離散化で,グリッドはサークルパターンで特徴付けられます.
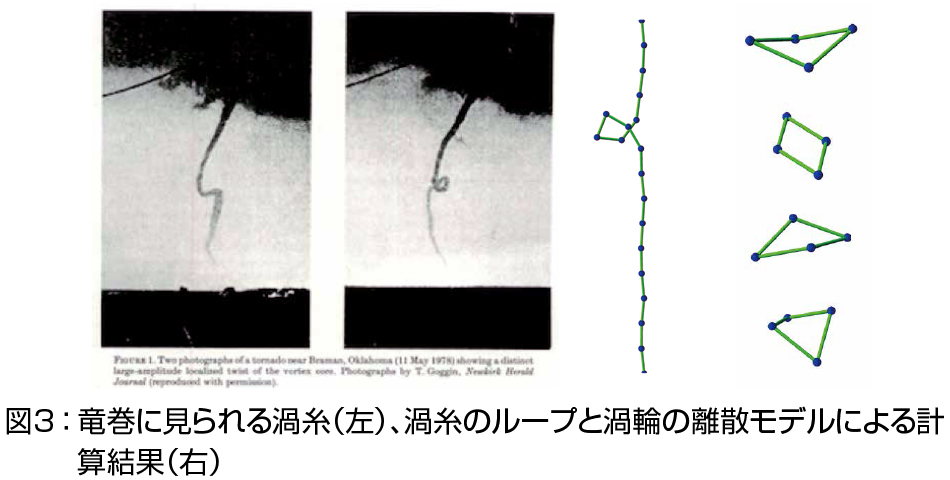
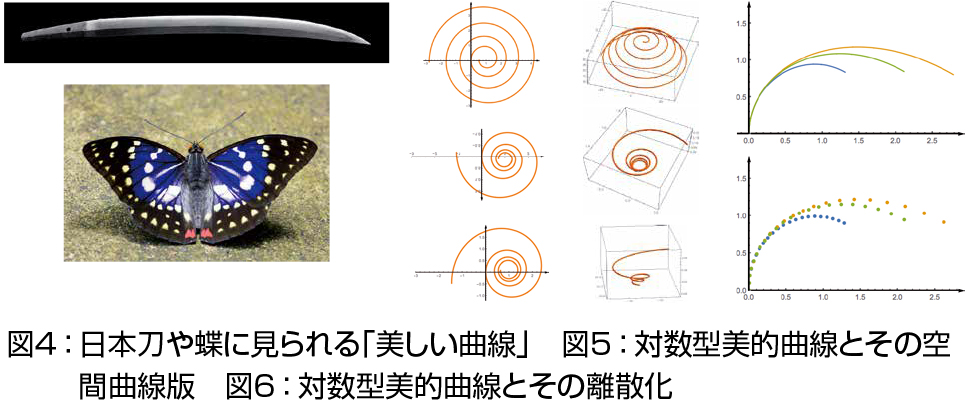
3. 離散可積分微分幾何と幾何学的形状生成:空間中の曲線・曲面やその変形を記述する基礎方程式としてさまざまな可積分系が現れることが知られています.さらに最近,離散可積分系と整合する曲線・曲面論の構築が進み,私は幾何学的形状生成,特に何らかの意味で「よい」曲線・曲面の生成の研究を工業意匠設計や建築の専門家と協力して進めています.図3は天然の渦糸である竜巻と,その離散モデルの計算結果.背後の構造を保存しているので,コストの低い計算で高品質な結果が得られます.図5(左)は工業意匠設計において,美的要素をもつ形状要素として日本で提唱された「対数型美的曲線」と呼ばれる平面曲線の族で,日本刀や蝶の羽など,私たちが「美しい」と思う形状から抽出されました(図4).最近,私たちは可積分幾何の立場から全く新しい理論的枠組みを提唱し,それを用いて構造を保存した,高速生成可能で高品質な離散化や(図6),空間曲線への一般化を構築しました(図5(右)).この理論を曲面に拡張し,得られた美的要素をもつ曲線・曲面の族を幾何学的形状要素として実装し,意匠設計での標準化を目指して研究を進めます.これらの形状は「美しさ」という人間の感覚の要素を取り込んだ数理モデルとしても重要な例です:よい方程式は,よい形状を生成する.
理論計算機科学とその応用

溝口 佳寛
学位:博士(理学)(九州大学)
専門分野:計算機科学
グラフ構造は,複雑な状況を直観的に説明するための基本的な道具として計算機が生まれる前からその構造についての研究や応用が行なわれていました.計算機誕生後は,計算機の内部表現(データ構造)としてプログラム中でグラフが利用されるばかりか,グラフそのものを変換して計算を行なう新しい計算システムなども考案され,従来の静的なグラフ構造の研究(グラフ理論)だけではなく,グラフを操作することに対する性質の変化を究明する研究(グラフ変換理論)が特に重要になっています.また,グラフ変換操作を既存の電子計算機上で実現することを前提にするのではなく,ある種の基本的グラフ変換操作がハードウェア的に実現された計算機を想定してのアルゴリズム構築の視点も必要です.特に近年は,分子計算や量子計算等の自然計算の枠組みでの計算機の立案・設計についても研究が進められており,グラフ変換による計算の基礎理論の必要性が高まっています.
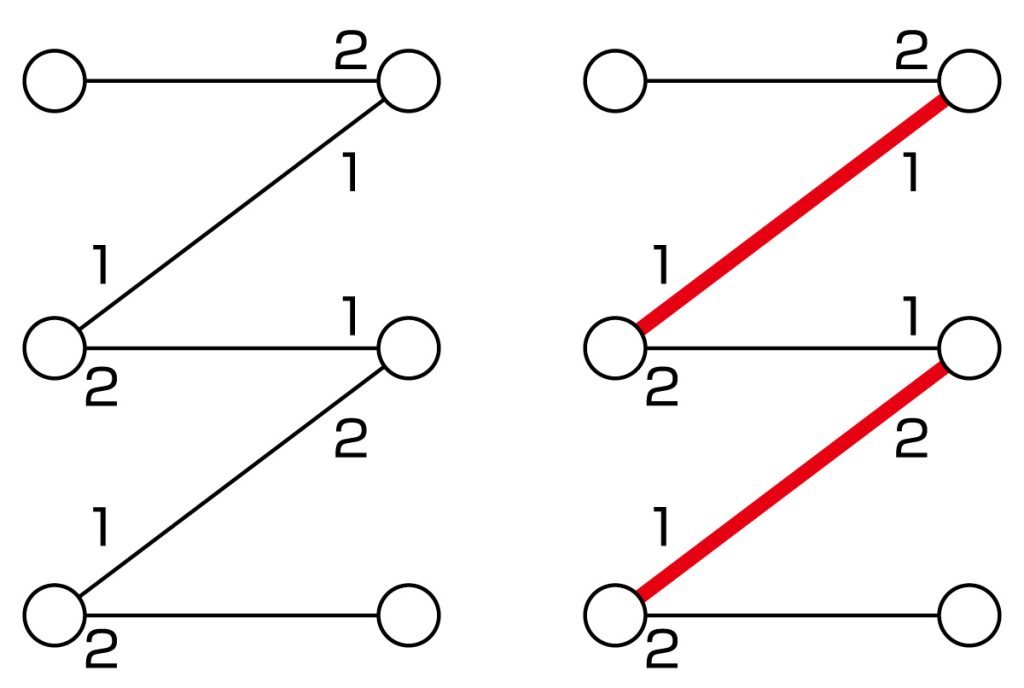
計算機による数式処理は数式を木構造で表現しパターンに適合した部分木を書き換えることにより式の計算や変形を行います.数式中の同一の項を共有するグラフ構造で式を表現しグラフ変換を行うことで計算効率を上げることが可能になります(図1).そこでは,グラフ構造のパターン照合アルゴリズムや式の意味を変えないグラフ表現方法が重要になります.
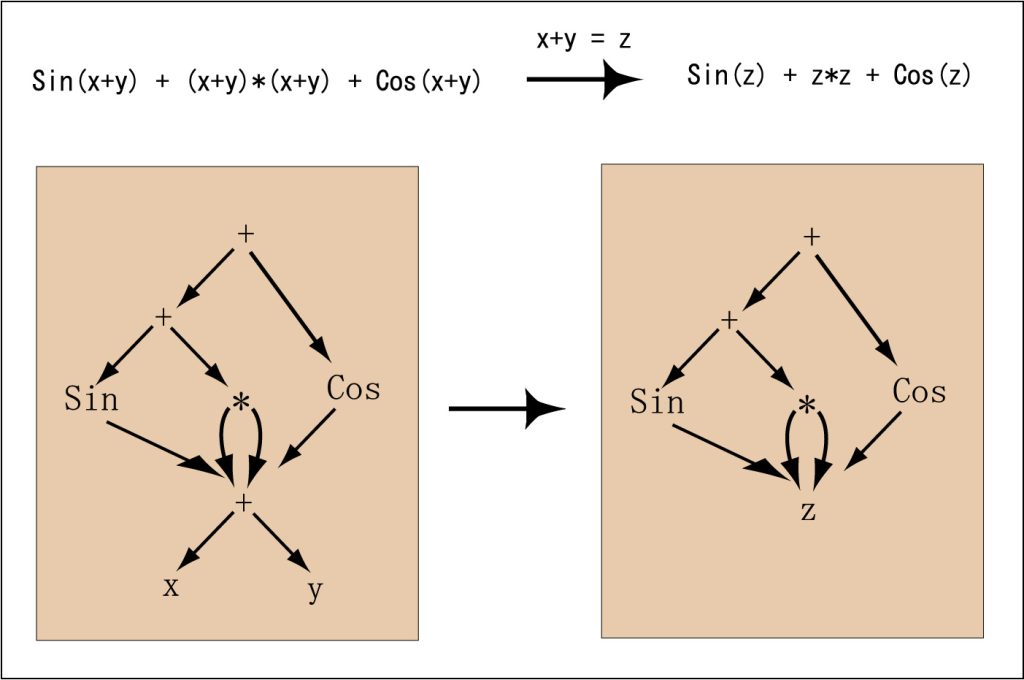
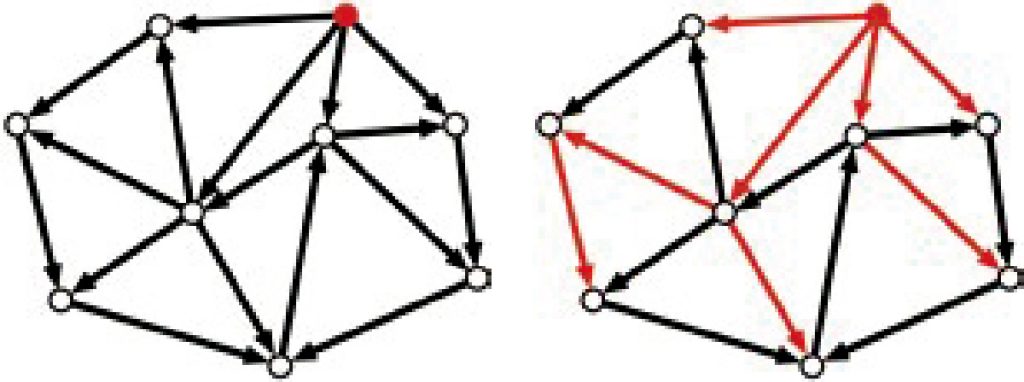
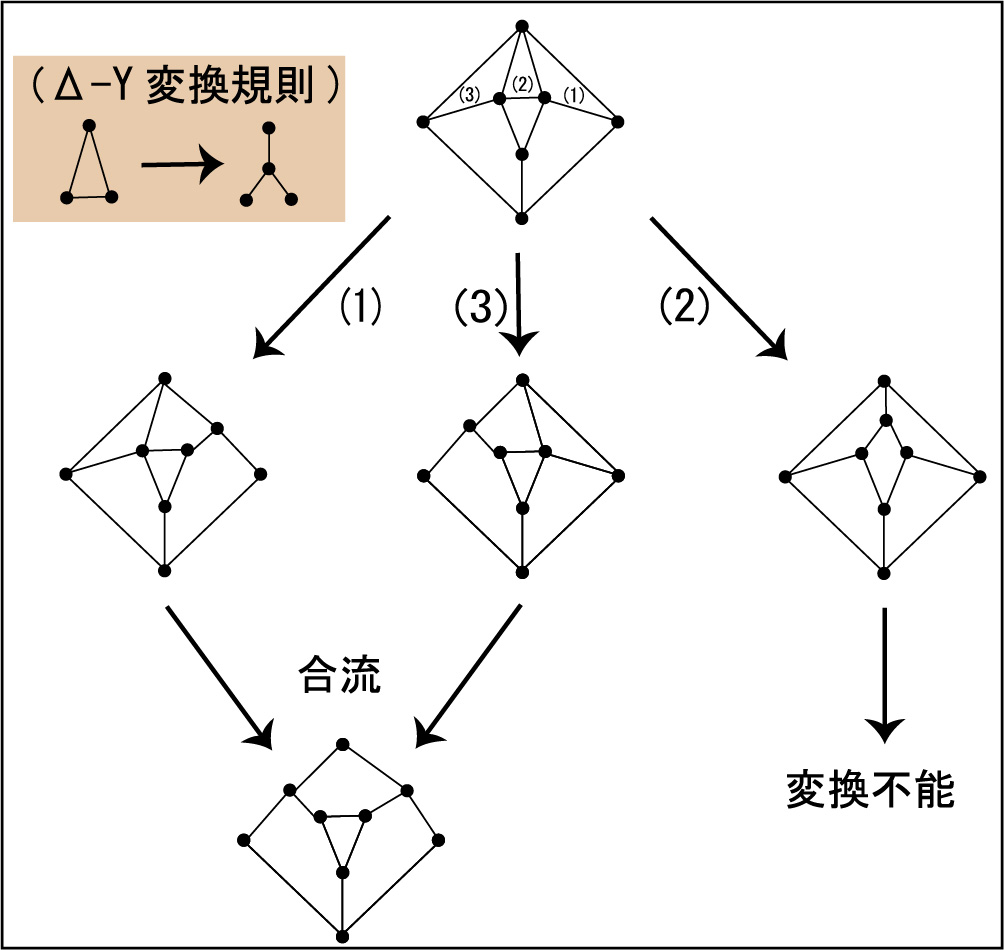
グラフ変換は変換計算領域に重複がない限り同時並列計算が可能です.交通網等における最短経路の計算,情報通信ネットワークにおけるネットワーク信頼度の計算,電気回路におけるインピーダンスの計算などには,グラフ変換を利用した計算アルゴリズムが開発されています.変換を利用した計算は変換規則の適用場所や適用順序により計算過程が分岐するため,いつも同じ計算結果が得られるとは限りません(図2).その計算の分岐が必ず合流することを理論的に証明すること,あるいは,同等の計算を行う必ず合流する変換規則群を導くことが重要になります.
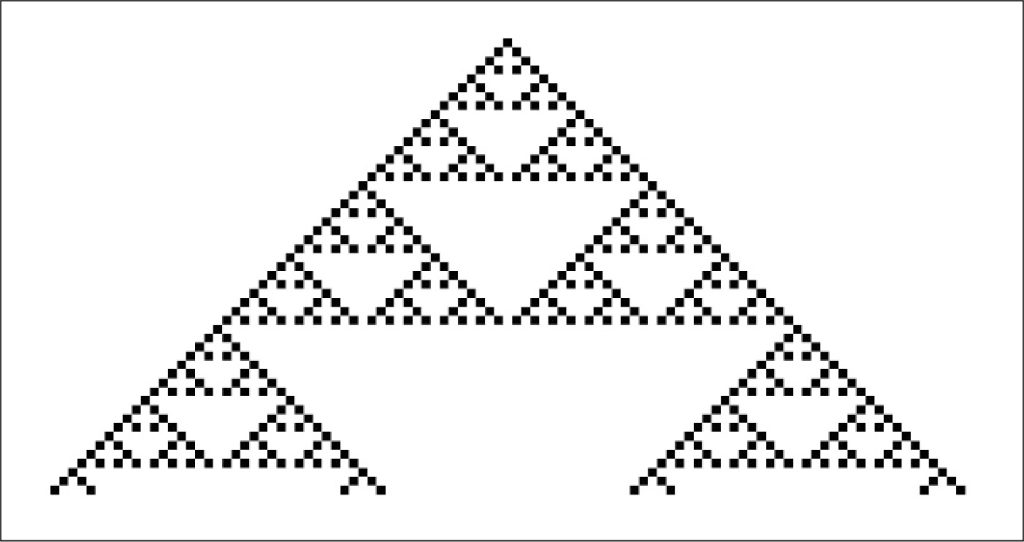
直線状に並んだ頂点をつないだグラフの変形による計算は非線形の物理現象のモデルとして応用されているセルオートマトンによる計算と深く関わりがあります(図3).セルオートマトンの計算機構を直接実現する素子の可能性として,遺伝子等のDNA鎖を用いた分子計算による実現が考えられています.グラフ変換系やセルオートマトンの計算可能性,計算万能性,計算等価性の判定などの理論は,実現される計算機の能力の有効性を評価します.
グラフ変換の同時並列計算の定式化や計算の合流性の証明には,離散数学,二項関係による関係計算理論,そして,圏論などの代数的手法が必要となります.また,計算能力の評価については,オートマトンや言語理論,計算量の理論,そして,数理論理学が必要となります.理論計算機科学は,現在の電子計算機を効率良く利用するための,データ構造やアルゴリズムの理論だけでなく,新しい計算機構の立案・設計を支援するための理論でもあります.
現在の情報化社会を支える電子計算機の利用技術革新や次世代の新しい計算機構開発を支えるための数学,理論計算機科学の研究を行います.
生物に学ぶ適応ネットワーク理論

手老 篤史
学位:博士(理学)(北海道大学)
専門分野:数理モデリング,適応ネットワーク理論
生物は長く過酷な生存競争を生き延びてきただけあって,生命現象の内には巧みで洗練された技術が多くあります.私の研究ではこのような生命現象を数式で書き表すことによって生命の持つ技術を理解・抽出し,工学・工業的な応用へと繋げる事を目標としています.
鉄道網や蟻の列,血管網に葉脈など,輸送に関する様々なネットワークがあります.これらは全て使われている経路が発達し,使われて無い経路は縮退していく性質があります.このようなものを適応ネットワークと呼びます.これらの適応ネットワークの形状は状況に応じて最終的な形状が(毛細血管や大動脈のように)大きく異なります.このような適応ネットワークの形成を理解することが本テーマの目的です.
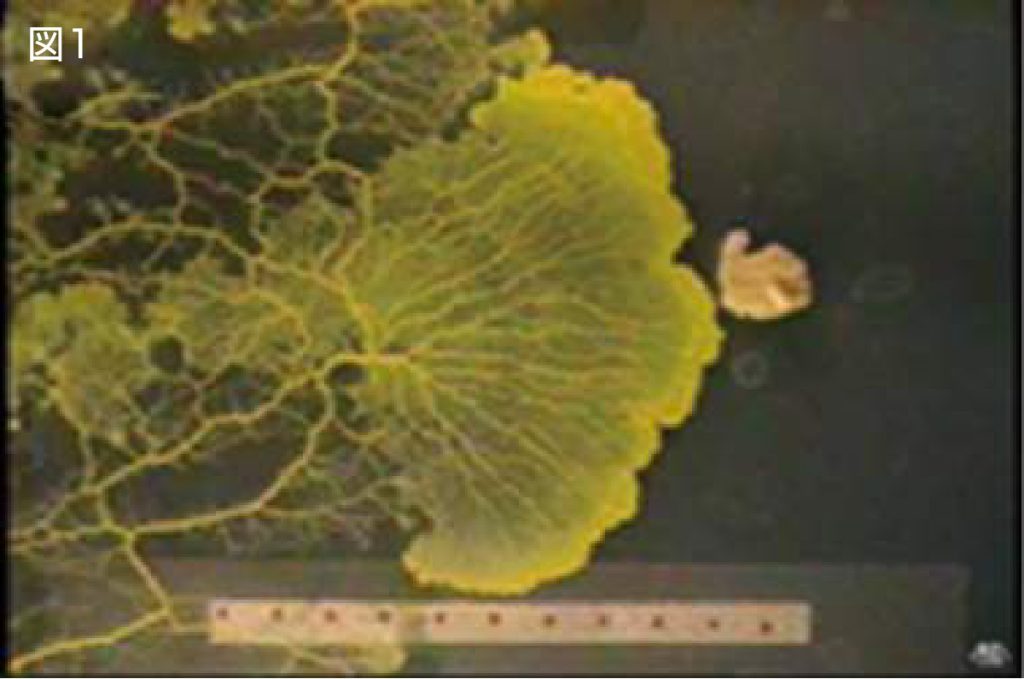
私がこの研究に用いた生物は真正粘菌変形体という生き物です(図1).粘菌は単細胞生物ですが,体内に栄養等を輸送する適応ネットワークを持っています.また,内部に核をたくさん持った集団的な性質も持った生き物です.例えばナイフで幾つかに切断すればそのそれぞれが別個体として生存できるし,反対にくっつけてしまえば1つの個体として生活することができます.粘菌はこのように切ったり貼ったりが自由にできることから適応ネットワークを理解するのに優れた素材になっています.この粘菌が作る輸送ネットワークは迷路を解き,最適なネットワークを求めるという実験が共同研究者の中垣俊之教授(はこだて未来大学)により行われました(図2a-c).しかし脳が無く自分の周りの情報しか持たない粘菌がどのようにして大域的な情報が必要なネットワーク問題を解くことができたのでしょうか.
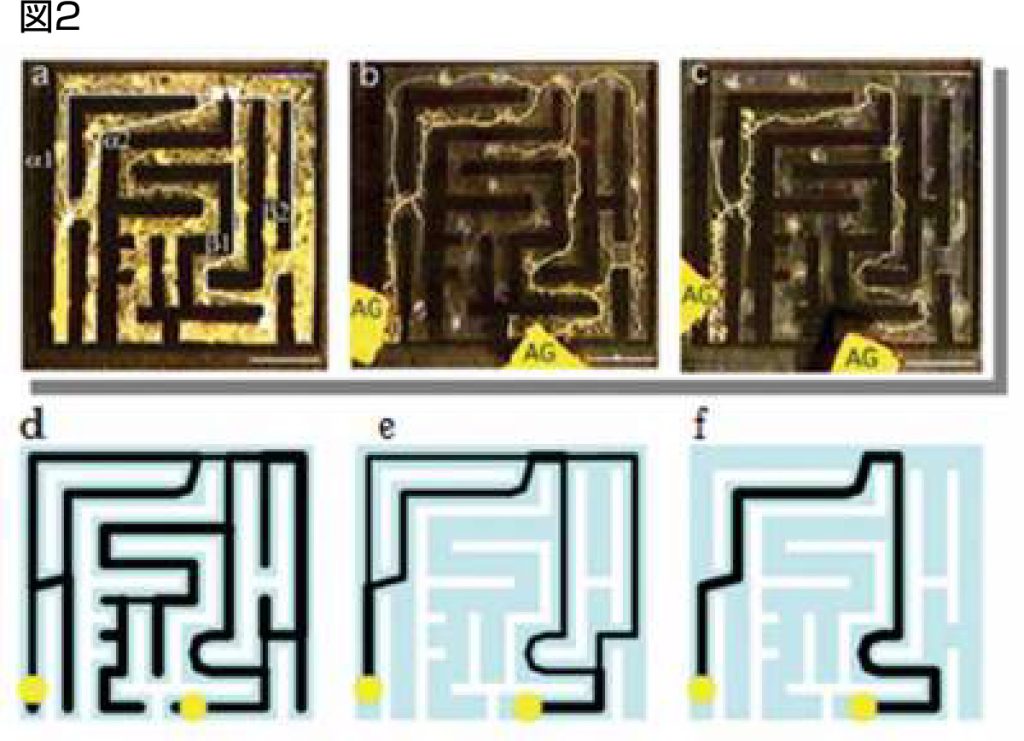
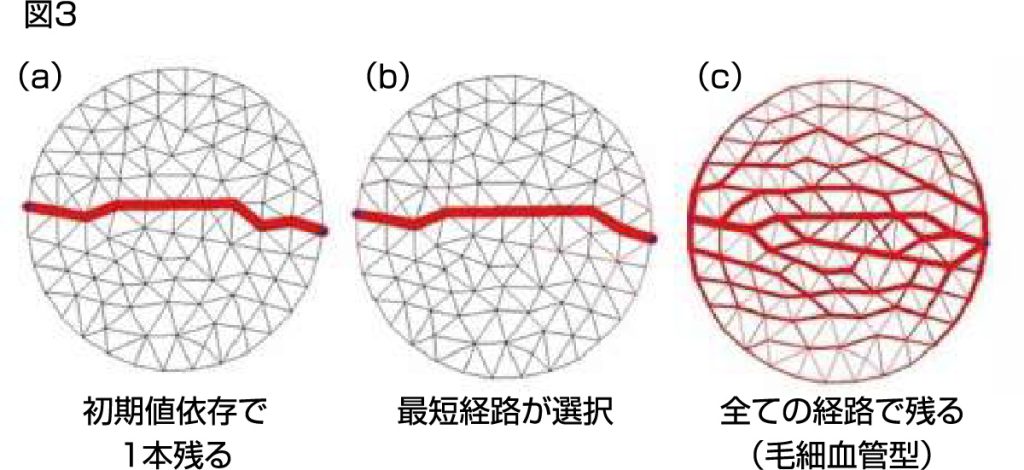
私はこの現象を数式で表すことによりこの現象を再現しました(図2d-f).その結果,この最短経路解が求まるパラメータを境界にしてネットワークの形が大きく変わることがわかりました.適応ネットワークの成長率が太い経路ほど強かった場合,図3aにあるように経路は1本だけ残ります.これは初期状態で太い管が成長しやすく,その後,より一層成長しやすくなっていくからである.反対に太い経路ほど維持コストが高ければ太い管は細い管に血流を奪われてしまい,全ての経路が残ります(図3c).このように粘菌が迷路を解くという研究の私の数理モデルはこの2つのネットワーク形成の境界を与えているのです.このためネットワークトポロジーが変化する場合には必ず図3bの状況を通過するので,適応ネットワークの組み換えを知るには図3(a-c)のパラメータに注目すれば良いのです.
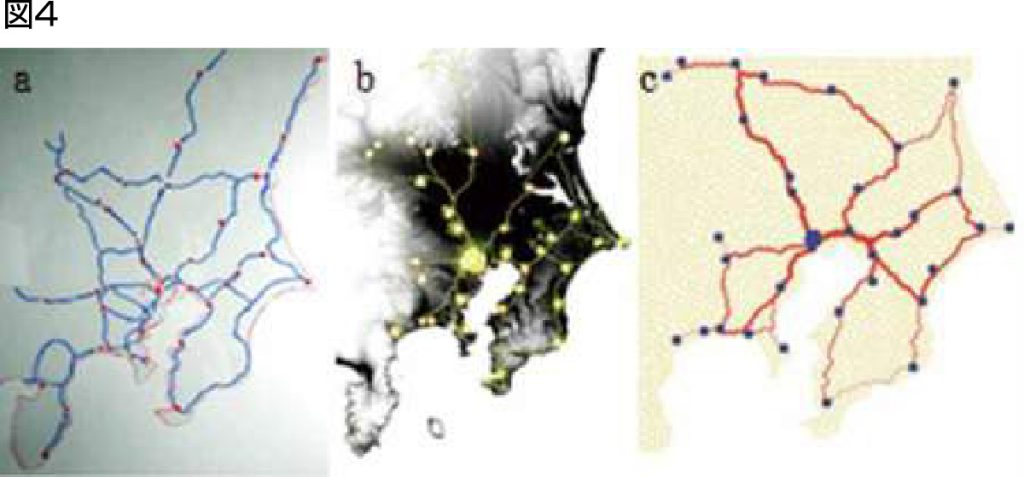
このようにして適応ネットワークの共通法則が得られたため,それを一般の鉄道網に応用しました(図4a-c).これからはさまざまな適応ネットワークに対してこの共通法則を応用し,工学・実用的な結果へと繋げていくことを目標とします.
また,他にも生物の多様なリズムを用いた行動制御や生物の自発的な形態形成についての研究も行っております.
最適化を基本とした研究・教育活動を目指して

脇 隼人
学位:博士(理学)東京工業大学
専門分野:最適化理論, 連続最適化
自然界のみならず,社会活動や日常生活においても,「最適化」が現れるので学ぶ価値のある研究分野といえよう.最適化の中でも,連続量を扱う最適化を連続最適化と呼び,私は主に連続最適化を対象として研究や教育を行っている.例えば,大学一年生の微分積分学で習う「ラグランジュの未定乗数法」は連続最適化で議論される手法の一つである.以下では,私が携わった研究・教育および産学連携について簡単に紹介する.
これまで凸最適化,特に,行列変数を持つ半正定値計画問題と呼ばれる最適化問題を中心に研究をしてきたが,IMIに来るまでは,半正定値計画問題を使って別の最適化問題を解くアルゴリズムを提案・実装する研究に取り組んでいた.現在は, もう少し半正定値計画問題に関して理論寄りの研究にシフトしている.具体的には,制御理論で現れる最適化問題に対して,得られる半正定値計画問題をテーマに研究を行っている.この半正定値計画問題はしばしば悪条件になることがあるのだが,それがシステム論の言葉で記述できることに気づき,それ以来このテーマに取り組んできる.調べてみると双対問題が興味深い数学的構造を有しており,幾つか論文を書いている.「最適化理論の深化よりも, 他の研究分野でどうやってうまく最適化理論を使うか」,ということを考えることが性に合っているようだ.
学生指導においては「分野の縮小再生産はしない」と考えていて,できるだけ自分の守備範囲の外の最適化について研究してもらっている.例えば,整数計画問題の応用およびそのためのアルゴリズムの開発などがそれにあたる.幸い,学生が優秀なためこちらがいろいろと教わって論文を一緒に書いている.
理学部数学科では最適化を教える講義がないが,大学院では用意されている.こちらもできるだけ幅広くテーマを選んでいて,最適化理論の基本を重点的に教えている.
これまで,IMIのシステムを利用して,自動車業界,製造業,行政などと幾つかのテーマで研究費をもらって共同研究を行った.いわゆる産学連携である.私の方針としては,学生に補助はしてもらうができるだけ一緒に手を動かすようにしている.学生を安価な労働力と捉えられないようにするためだ.
このように取り組んでいると,産学連携についてはいつも難しさを感じている.その一因は,「論文を書いて自分たちの獲得した知を後世に残す」という共通認識を持てないところにある.我々にとっては当たり前の思想であるが,相手側は必ずしもそうではない.産学連携を通じて産業界・教員および学生が論文を書き,その学生が学位を取り,学術界・産業界で活躍してもらうのが産学連携の理想だと考えている.この理想に同意してもらえる相手と優先的に共同研究を実施しようと思っている.
双曲型偏微分方程式の逆問題

髙瀬 裕志
学位:博士(数理科学)(東京大学)
専門分野:偏微分方程式,逆問題,幾何解析
双曲型偏微分方程式は解の有限伝播性やホイヘンスの原理等重要な数学的特徴を持つ。数理科学の分野での重要性はもちろんのこと、力学や波動をはじめとする様々な自然現象のモデル化が可能であるため、これまで物理学や工学の分野においても重要な役割を担ってきた。中でも、存在する解の情報から支配される方程式系を決定する逆問題は、数理科学の分野では非適切性問題として極めて重要である。加えて物理現象の背景を詳細に理解できるツールとしても強く注目されている。
偏微分方程式の逆問題における代表的な研究課題は、未知の波源を特定する波源項決定逆問題と、方程式が記述する未知の物理的性質を特定する係数決定逆問題である。考えている領域の一部で波動を観測した観測者が、これらの未知量を観測領域の近く或いは考えている領域全体で特定できるかどうかを調べることが目的となる (図1)。

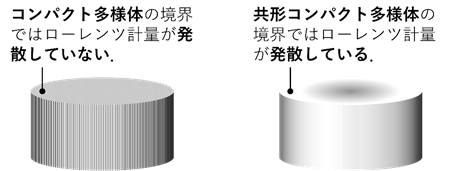
様々な偏微分方程式のタイプがある中で、特に双曲型偏微分方程式は座標に依存しない幾何学的な記述が可能である場合が多い。したがって例えば不定値な計量を導入した擬リーマン多様体上における解析との相性が非常に良い。近年では逆問題の様相を幾何学的視点から捉えるべく、コンパクトなローレンツ多様体上の幾何解析を用いた研究が進められている。さらに、物理学からの要請として多様体の境界で計量が発散する共形コンパクトな多様体上での逆問題解析も注目を集めている(図2)。共形コンパクト多様体上では方程式の主要部が退化するため解析が容易ではなく、退化型方程式に対する新たな逆問題理論の構築が必要である。
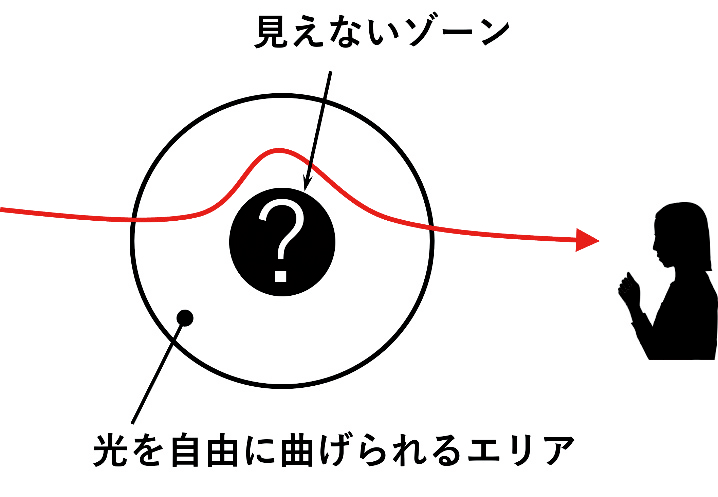
結果の原因となる未知量を特定する逆問題は、当然ながら必ずしも肯定的に解決されるわけではない。否定的な例として、映画「ハリー・ポッター」に出てくる透明マントのような光のクローキング技術がある。これは、ある対象の周りの有界な領域において媒質を変化させることで光の進行を曲げ、外部からの光が伝播しない見えないゾーンを作り出すことでその対象を不可視化する技術である (図3)。偏微分方程式論において媒質の変化はしばしば低階項であるポテンシャルとして定式化される。見えないゾーンにおいてはそのポテンシャルの影響により外部から光が伝播しない状況を、ポテンシャル項付き波動方程式のコーシー問題の観点から理解することもできる。このように否定的な状況を改めて考察することが数学的に面白い構造を発見する上で助けになることもあるのかもしれない。
代数解析: 数学の落ち合うところ

落合 啓之
学位:博士(数理科学)(東京大学)
専門分野:代数解析
私の研究分野は代数解析学で,特にD加群を用いた研究を主としています.初期の頃,修士論文ではある非ホロノミー系を満たす佐藤超関数を調べ,学位論文ではあるホロノミー系を満たす半単純リー群の大域指標の定める輪体を調べました.もう少し先を説明するために,私の経歴を簡単にまとめてみます.1998年,それまで9年間お世話になった立教大学を離れ,九州大学に赴任しました.3年後に東工大へ移り,さらに2002年の秋に名大へ異動,そこで7年を過ごし,2009年の秋からまた九大に戻ってきました.この間,概均質ベクトル空間,1変数ならびに多変数の超幾何関数を始めとする特殊関数,そしてゼータ関数と出会います.私自身は佐藤幹夫氏の直接の指導を受けたことはないのですが,無意識のうちにその影響下にいると思っています.ゼータ関数も研究の対象にしていますが,強いて言えば,私自身の
興味は,数に対するものよりも関数に対するものといえるでしょう.今まで論文の対象としてきたものも,関数で表わせるものやそれらの間の関係式として表わせるものが多いと思います.そして,関数そのものとそれを決定・記述する様式の双方からアプローチしています.これが代数解析的な手法の特徴のひとつです.また,図形全般に対する興味はともかくとして,不変式論,ならびにその双対と言える軌道分解には,研究の初期の頃からかなりの思い入れがあります.座標を使わない内在的な叙述と座標を使った明示的な記述を,あえて片方だけで徹底したり行ったり来たりしたり,あるいは組み合わせ的技法を絡めたりという部分に面白みを感じています .今やKazhdan-Lusztig 予想も常識のようになりつつあり,見渡せる景色は前世紀よりも確実に広くなっていると思います.
このパンフレットはIMI に関するものですから,私とマス・フォア・インダストリとの関わりについて説明します.2010年4月に,GCOEの事業推進担当者のひとりである岩崎克則氏が北大へ転任したため,岩崎氏のつとめていた「機能数理の基礎」ユニットの事業推進担当者を引き継いだことで,マス・フォア・インダストリとのつながりが始まりました.このたび,IMIの発足に伴い,数理学研究院を1年半で再び離任することとなったのは残念ですが,「転んでも起きない」という不屈の精神で新地へ向かいたいと思います.私の今までの活動のうち,社会との接点と言えるのは,数学が伝統的に社会と向き合ってきた諸分野のうちのいくつかですが,数学の社会への情報発信や連携は機会をいただいてつとめています.例えば,高校教育(のうち,おもに入試問題説明会や教科書の編集に関すること),保険数理(アクチュアリ会の研究会員),執筆(数学セミナーや数学小景などでの数学の平易な紹介),講演(公開講座,市民講座)などです.昨年度から安生健一氏を代表者とするクレスト(科学技術振興機構)の『デジタル映像数学の構築と表現技術の革新』の九大班の班員もつとめています.
近年は幾何学的表現論の枠組みで積分が果たす役割を中心に研究を進めています.日本数学会では函数解析分科会の「表現論と調和解析グループ」に属していますが,必ずしもその範囲に限らない対象や手法にも興味を持って活動して来ました.今後も柔軟に数学をして行きたいと考えています.

トポロジーとその応用

佐伯 修
学位:博士(理学)(東京大学)
専門分野:位相幾何学,トポロジー,特異点論,微分位相幾何学,DNA結び目
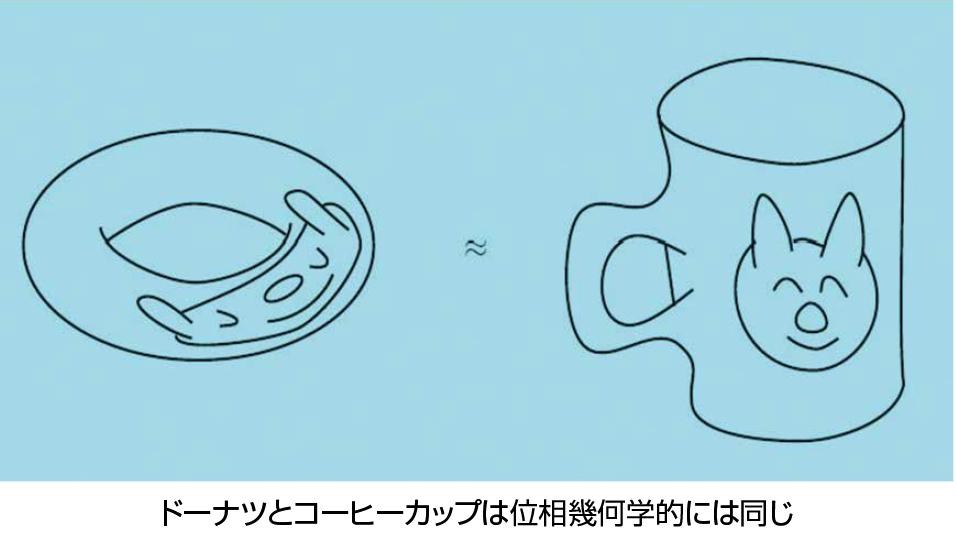
位相幾何学(トポロジー)とは、図形をゴムのようなものでできていると考え、グニャグニャと連続的に変形できるものは同じと思う、とても柔らかい幾何学のことです。言い換えると、幾何学的対象の性質のうち、それを連続的に変形しても変わらないものを研究する、純粋数学の一分野です。たとえばコーヒーカップとドーナツは位相幾何学的には同じものと考えられます。それらには「穴」がちょうど1つずつありますが、この「穴」の個数は、図形の連続変形で変わらない量の1つの典型的な例となっています。
こうした位相幾何学は、図形が柔軟性を持つ場合に威力を発揮します。その最たるものが、紐を結んでできる結び目や絡み目です。紐を結ぶことは日常生活でも重要な行為で、結び目が原始時代から人間の生活と深く結びついていることは間違いありません。実際、野生のゴリラも結び目を作ることができることが知られています。ごく最近になって、こうした結び目が、DNA(デオキシリボ核酸)の研究に深く関わることが明らかになってきています。
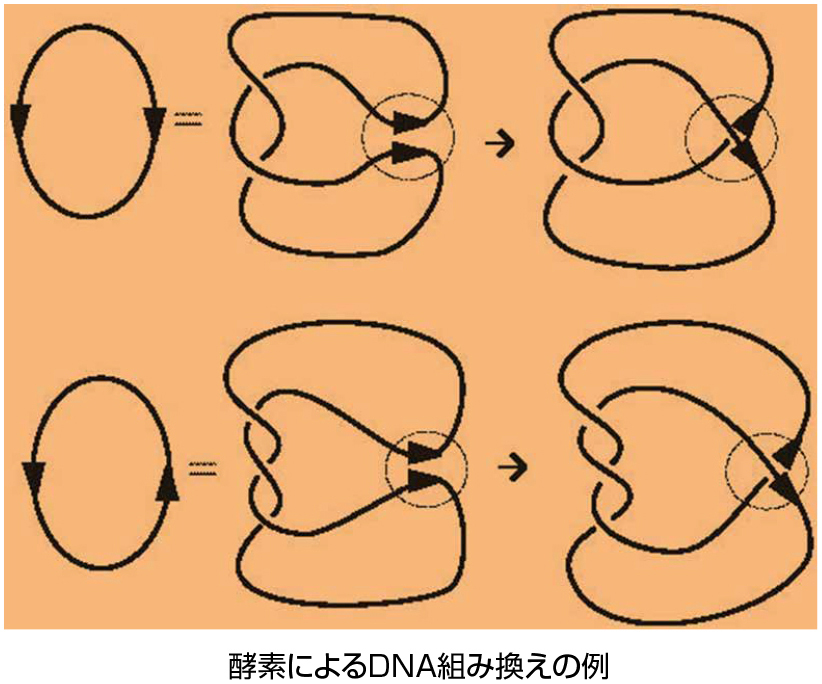
遺伝情報の担い手であるDNAは、生物の細胞内で捩れた紐状の形をしていて、輪になっていることもあり、さらにそれが結ばれたり絡んだりしていることもあります。こうしたDNAの結び目・絡み目は、酵素の働きによって作られることは知られていましたが、その仕組みの詳細については実験技術の限界のために明らかにされていませんでした。1980年代終盤、数学者のC.ErnstとD.W.Sumnersは、数学、特にトポロジーにおける結び目理論の最新の結果を駆使してその酵素の仕組みを解明しました。もともと結び目理論は19世紀のGaussによる電磁気学やKelvin卿による渦原子仮説に端を発すると言われていますが、その後化学者・物理学者は結び目を忘れ、数学者だけが興味を持って研究してきた歴史があります。我々はその流れを受け、現代数学の中でも最近もっとも盛んに研究されている分野の1つである結び目理論を駆使することにより、トポイソメラーゼと呼ばれる酵素によるDNA組み換えの解析を、数学的側面から研究しており、こうした解析の産業技術への応用も目指しています。
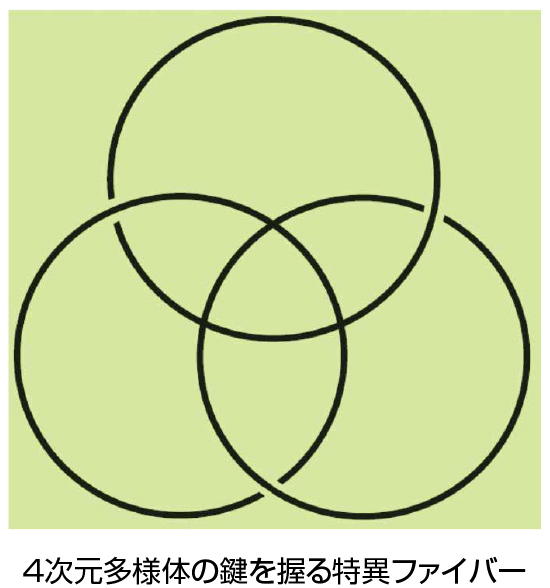
なお、こうした研究と同時に、可微分写像の特異点論も活発に研究しています。特に、滑らかな物体間の写像の特異点が、そうした物体の位相幾何学的性質を深く反映する具体的事実などを数多く発見してきています。特に、特異ファイバーと呼ばれる1点の逆 4次元多様体の鍵を握る特異ファイバー像に着目する研究では世界的な第一人者を自負しており、それを最初に定式化した著書も出版しました。最近はこうした理論を、多値関数データのための視覚的解析に応用すべく、研究を行っています。
また、可微分写像の特異点論以外にも、位相的埋め込みの第一障害類、余次元1写像の分離性質、複素超曲面の孤立特異点の位相幾何、ファイバー結び目、4次元多様体、余次元1の埋め込み、空間曲線の微分幾何学的不変量、結び目解消数など、位相幾何学の様々な分野を幅広く研究しています。こうした研究は、種々の分野で応用できる可能性があり、たとえば物質・材料の性質をミクロなレベルから考察する際には威力を発揮することが期待されます。なお、一般化されたフィボナッチ数列の漸近挙動についても精力的に研究を行っており、解析関数の零点に関する研究もあります。
こうした幅広い研究を行っていることは、教育に対する効果もかなり大きく、これまでに指導した学生の産業技術への貢献実績もあります。また、異分野連携で活躍する数学博士人材を育成するための卓越大学院プログラムのコーディネーターも務めております。
今後も、トポロジーという純粋数学を基に、数学と産業技術の関わりを深めてゆければ誠に幸いです。
確率論とその応用

白井 朋之
学位:博士(数理科学)(東京大学)
専門分野:確率論
ルーレット,双六,宝くじ,株価の値動きなど,確率的現象は日常生活においても身近に観察できるものです.これらの現象(対象)には自然に確率的な要素が備わっていますが,一見ランダムな要素がまったくないように見える問題にもランダムな側面があったり,意外な形で確率論的手法が使えることがあります.ここではそのような例を3つばかり紹介します.
(1)日本では「角谷予想」,海外では「コラッツ予想,3n+1問題」などと呼ばれる初等整数論の有名な未解決問題をご存知でしょうか? 任意に選んだ自然数に対して,「自然数が偶数ならば2で割り,奇数ならば3をかけて1足す」という操作を繰返すと必ず最後は1になるという予想です.例えば,初めに7を選んだとすると,7,22,11,34,17,52,26,13,40,20,10,5,16,8,4,2,1となります.2009年の時点で20×258以下の自然数に対しては,コンピュータによって予想が正しいことが確かめられています.この問題自身にはどこにも確率的要素はありませんが,実はランダムな構造が潜んでいます.
(2)以下の文字列は,単純換字暗号とよばれる古典的な方式で,ある文章を暗号化したものです.つまり,aをf に,bをtにというように,aからzの順番を入れ変えて一対一に対応させることによって暗号化しています.
fyeaxjqfzjoxceddedcjbujcxbjhxgpjbegxrjukjzebbedcjopjsxgjzezbxgjudjbsxjofdljfdrjukjsfhedcj
暗号化の方法が上の方式であるとわかっているとすると,マルコフ連鎖という確率論の基本的な道具で(ある程度)解読することができます.以下はその実行例です.

Googleなどの検索サイトの人気ページのランク付けにもマルコフ連鎖が使われていることはよく知られています.
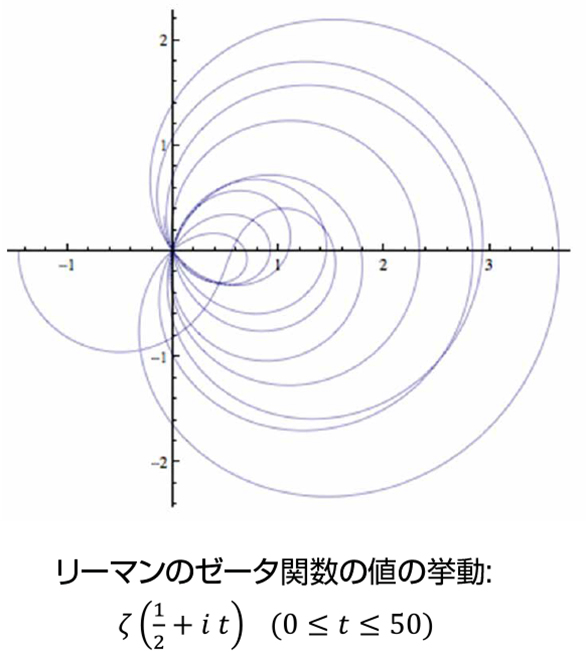
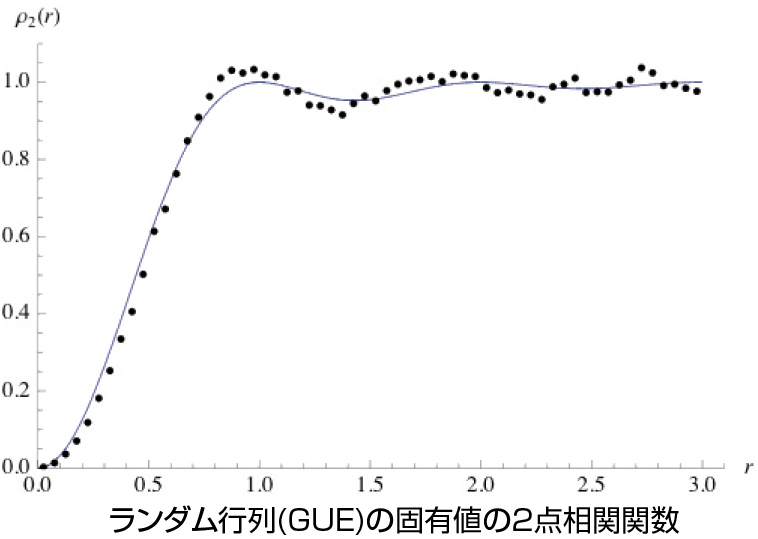
(3)2000年にアメリカのクレイ数学研究所が,ミレニアム問題として100万ドルの懸賞金をかけて7つの問題を提出しました.そのうちの一つであるポアンカレ予想は最終的にはペレルマンによって解かれましたが,いわゆるリーマン予想は未解決の難問です.リーマン予想とは,$\zeta (s)=\sum ^{\infty }_{n=1}\frac{1}{n^s}$ で定義されるリーマンのゼータ関数とよばれる複素関数の(非自明な)零点はすべて Re$(s)=\frac{1}{2}$ という線上にあるだろうという予想です.この問題にもランダムな要素はまったくありません.しかし,多くの理論的考察やシミュレーションなどにより,その零点達があるランダム行列の固有値と同じ振る舞いをすることがわかってきています.
私の興味の一つは,上に挙げたような一見ランダムには見えない現象の裏に潜むランダムな現象を見つけて,それを確率論的手法を用いて研究することです.
(1)の問題は1960年代に数学者の角谷静夫先生が興味を持たれて,イェール大学の同僚に伝えたところ,イェールの数学教室では一ヶ月くらいの間皆がこの問題に嵌ってしまったそうです.他の大学でも同じような現象が起こり,一時期流行ったゲーム「テトリス」と同じように,数学の研究を鈍らせるための某国の陰謀だったのではないかという笑い話もあったそうです.
(2)であげた問題は,アメリカのある州立刑務所の囚人の書いた壁の落書きが何を意味するのかを調べるために,刑務所の心理学者によってスタンフォード大学統計学教室の技術相談窓口に持ちこまれたことがきっかけだったそうです.
(3)の研究の方向性は,プリンストン高等研究所のコモンルームでのティータイムに,物理学者であるダイソンから解析数論の研究者であるモンゴメリーへ述べられた一つのコメントから始まりました.数学者レンニは,「数学者とはコーヒーを定理にかえる機械である」と言ったそうですが,一杯のコーヒー(紅茶?)が重要な研究の方向付けをした場面でした.
IMIにおいても,自由な発想により実りある異文化間の交流ができることを心から願っています.
数理科学的観点からの血糖値管理
小谷 久寿
学位:博士(数理学)(九州大学)
専門分野:位相幾何学、整数論、数論的位相幾何学
ここのところ、私は他大学の医療分野の研究者や応用数学者の方たちと血糖値管理に関する分野の枠を超えた共同研究に取り組んでいます。もう少し具体的に書くと、これは手術後集中治療室(ICU)患者のデータを用いて、現実の医療現場に役立つような血糖値を管理するアルゴリズムの開発を目指した研究です。この研究は上に掲げている私の専門分野のお話とは異なるものですが、ここでは産業社会への数学・数理科学の応用を目指したIMI関連の研究として、それについてお話しします。
手術直後ICU患者は手術侵襲によるストレスや強心剤等による影響で血糖値の急上昇が見られます。高血糖は多臓器不全・昏睡・予後悪化等を引き起こす原因となるため、インスリン投与により血糖値を適正値内に維持することが重要であると考えられています。しかし、インスリンによる血糖値管理はインスリン作用の遅延やインスリン感度の時間変化等の様々な要因によりコントロールが難しく、さらにインスリン投与により逆に低血糖に陥ってしまった場合には深刻な予後不良を引き起こしてしまうという問題があります。現在、一定の条件のもとICUでの血糖管理は看護師によって行われていますが、標準的な管理アルゴリズムは未だに確立されておらず、血糖値のコントロールは看護師の経験に依る部分が大きいのが現状となっています。ただ、そうした血糖値管理は看護師の負担も大きく、手法の標準化が望まれています。
そこで、この共同研究では、数理的なアプローチと医療現場での知見とを組み合わせ、実際の医療現場で役立つような血糖値管理をアシストする標準的手法の開発や熟練看護師の投薬判断アルゴリズムの推定を行うことを一つの目標としています。
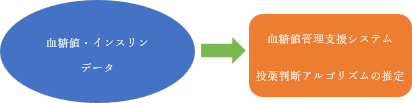
このような問題に対する数理的なアプローチとして、これまでにも血糖値管理に関連する血糖値・インスリンの数理モデル等が考案されてきましたが、生体における動態を表現する数理モデルには観測できない変数が多く含まれていたり、患者ごとに固有のパラメータを推定する必要がある等、難しさがあったり、それぞれできることや目的が異なっています。また、近年データ科学分野で様々な新しいデータ駆動型の研究手法が開発され続けています。この共同研究では、従来の手法と新しい手法を取り入れつつ、今回の研究の目的に即したより良いアルゴリズムの開発に貢献すべく努めています。
血糖値管理のような医学的知見が重要である共同研究においては、数学・数理科学的な立場だけからではなく、外科医師、ICU専門看護師を交えて協働的に研究を進めることが重要です。医療従事者の方々とのコミュニケーションを大事にしながら着実に共同研究を進めて、数学・数理科学の医療分野・産業社会への応用へと繋げていきたいと思います。
テータ函数で非自明な的を狙う

重富 尚太
学位:博士(機能数理学)(九州大学)
専門分野:可積分系、離散微分幾何学、応用物理学、テータ函数
楕円テータ函数というよい性質を持った特殊関数を一つの軸として(1)可積分系とそれに関連する幾何学、(2)応用物理学の研究をしています。楕円テータ函数は数多くの恒等式を満たすことや、擬二重周期を持つことで知られており、数学の幅広い分野に登場します。私の研究の場合、こういった性質は、可積分系の厳密解を構成することに活用できます。また逆に、解の情報から方程式を離散化したり、非自明な保存量を発見したりするときにも重要となってきます。以下、テータ函数の応用例について、具体例を交えつつ紹介します。
(1)可積分系とそれに関連する幾何学
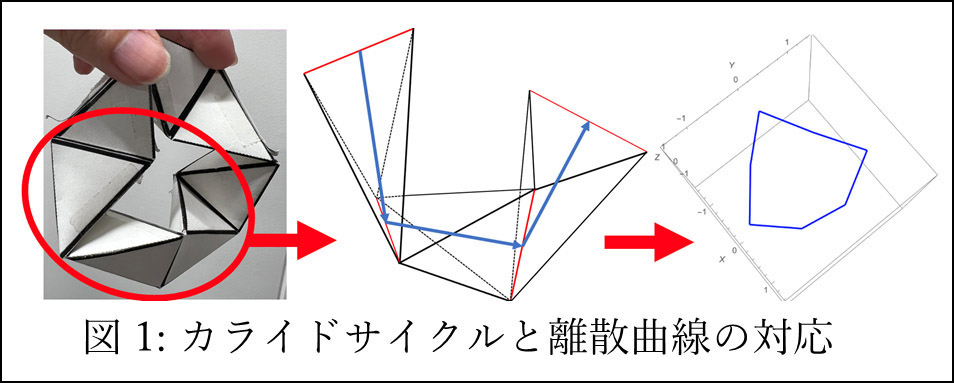
可積分系とは、非線形であるのにも関わらず、よく知られた函数で厳密解が構成できてしまう微分方程式の族のことを指します。また、解の性質を保つ離散化が可能であることも可積分系の著しい特徴の一つです。可積分系の応用例は様々なものがありますが、その中でも離散的な曲線や曲面の研究は、CGや建築、リンク機構などの産業的実用性が高い分野で活用できるという点で重要です。例として、メビウスカライドサイクルを挙げます。これは、6つ以上の合同な四面体を蝶番で環状に繋げて作るリンク機構で、変形の自由度が1であること、複数の保存量を持つことなどから、数学・物理学・工学的に大変興味深い機構ですが、通常、リンク機構の厳密な解析は容易ではありません。ところが、この機構を捩率一定の離散曲線として捉えれば(図1)、その変形が可積分系で記述されることが分かり、曲線の捩率や曲率のみならず、位置ベクトルまでもがテータ函数で明示的に構成できてしまいます。この結果により、これまで知られていなかった保存量などが発見されており、今後のカライドサイクルの解析で重要な役割を担うものと考えられます。
(2)応用物理学
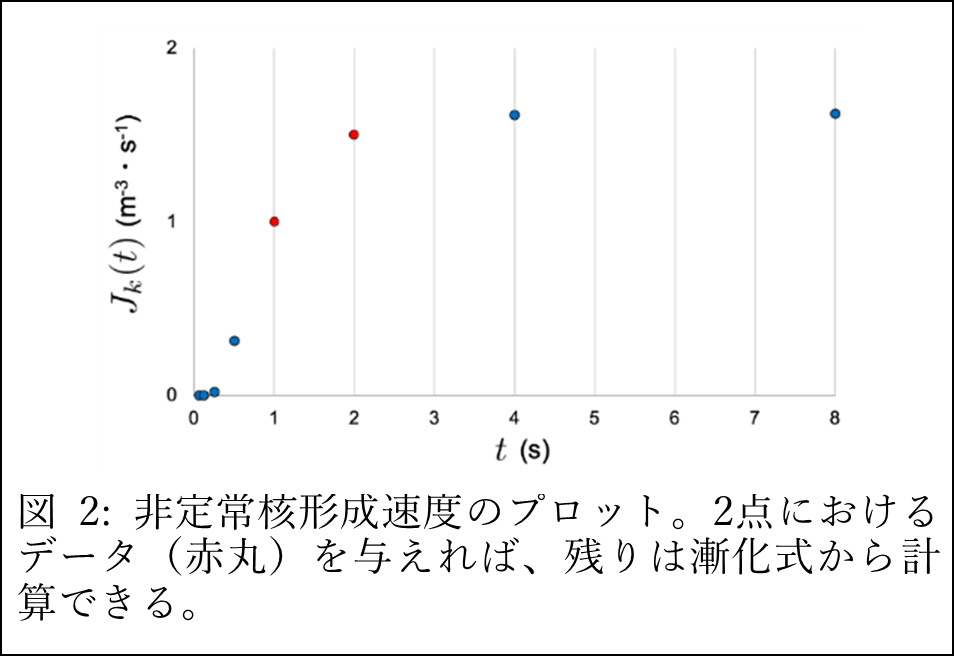
テータ函数は物理学の研究にも登場しますが、私の研究では、地球科学などに見られる応用物理学的な現象の解析にテータ函数の活用を進めています。例えば、核形成と呼ばれる現象は、発泡や結晶化に代表される物理現象であり、極めて身近に観察されるものです。定常過程に至るまでの再初期段階を非定常核形成と呼び、この現象を特徴づける量が非定常核形成速度 Jk( t ) です。この量の測定には、長時間にわたる実験が必要な場合があり、コストの面で課題があります。一方で、 Jk( t ) は楕円テータ函数の特殊値で表されることが1969年に指摘されていましたが、発表以来一度もテータ函数の性質を活用した研究はありませんでした。今回、テータ函数の恒等式を駆使することで、Jk( 2nt ) が満たす非自明な漸化式を導出し、少ないデータで Jk( t ) の値が推定できるようになりました(図2)。これによって、非定常核形成の実験研究におけるコスト削減が期待できます。
4次元図形の設計図:視えない次元を視る

濵田 法行
学位:博士(数理学)(九州大学)
専門分野:低次元トポロジー,曲面の写像類群,シンプレクティックトポロジー
私は、低次元トポロジーとよばれる純粋数学の一分野を研究しています。より詳しくは、4次元の図形を曲面の上に“描く”理論があり、この4次元と2次元が相互に影響し合う関係に強い魅力を感じ、研究しています。
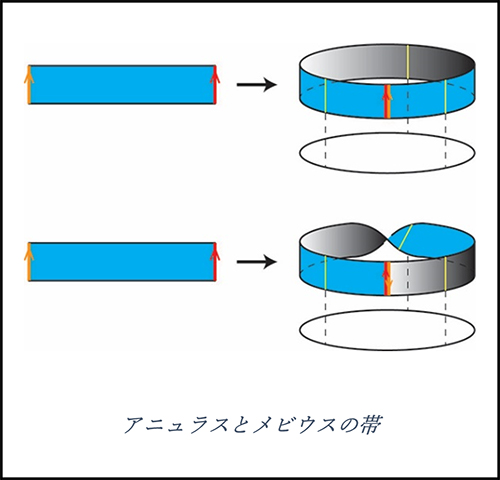
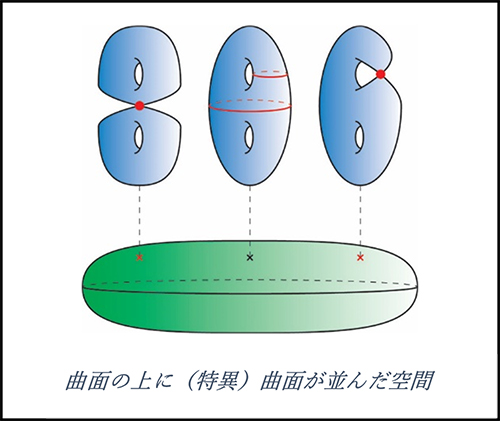
4次元を描く方法の説明の前に、次元を落とした簡単なモデルを見てみましょう。次の図のように細長い長方形の紐を用意して、両端を張り合わせることを考えます。張り合わせ方は二通りあり、一方からは普通の輪っか(アニュラスといいます)ができ、もう一方からは捩じった輪っか(いわゆるメビウスの帯)ができます。このとき図のように、アニュラス、メビウスの帯の下に仮想的な円周をそれぞれ置くと、円周の各点の上に短い線分が並んだような構造があることが見てとれます。円(1次元)の上に線分(1次元)が並んで、全体としては1+1=2次元の図形となっているわけです。
想像力を膨らませてこの考え方を発展させると、曲面(2次元)の上に曲面(2次元)が並んだ空間というものが考えられ、この空間の次元は2+2=4次元になります。さらにもう少し条件を緩くして、次の図のようにときどき特異点をもった曲面があらわれることも許すことにすると、非常に豊かなクラスの4次元図形(専門用語でシンプレクティック4次元多様体といいます)を扱えるようになります。
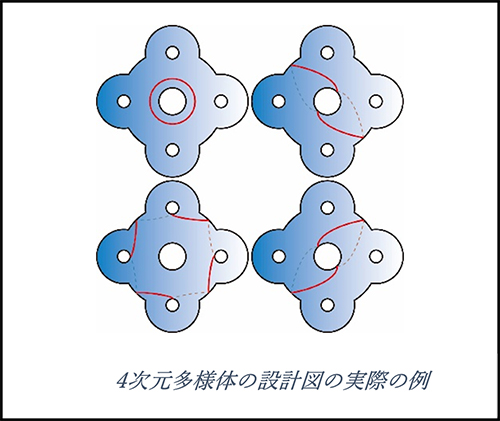
上に並んでいる曲面をファイバーといいますが、ファイバーの上に特異点に対応する閉曲線を描けば、考えている4次元多様体の情報をすべてもった「設計図」が得られます。もう少し正確には、この設計図はファイバーの曲面に付随する写像類群という群の言葉で記述されるものです。
こうして4次元多様体と曲面の写像類群が関係づき、4次元多様体の制約から写像類群の性質が得られたり、逆に写像類群の議論から4次元多様体の性質が得られたりと相互補完的な研究があります。
私がもっとも得意とするのは、上で説明した写像類群における「設計図」を作ることです。これまでに、基礎的な例をみつけたり、再利用が可能な使い勝手の良い設計図を作ったり、またそれらをもとに複雑な設計図を作ることで存在が知られていなかった4次元多様体を構成したりしてきました。
ところで4次元多様体の分類の仕方として、2つの多様体が“連続的に”移り合うとき同じとみなす同相の立場と、“滑らかに”移り合うとき同じとみなす微分同相の立場があります。この2通りの区別の違いは非常に繊細であり、4次元トポロジーでは中心的な話題です。近年の私の(共同)研究では、ある標準的な4次元多様体に同相であるが微分同相ではない4次元多様体というものを多く発見しており、4次元における同相と微分同相のギャップについての新たな知見を得ています。
トポロジーとその諸科学への応用

鍛冶 静雄
学位:博士(理学)(京都大学)
専門分野:位相幾何学,リー群,応用数学
私は図形をおおざっぱに調べるトポロジー(位相幾何学)という分野の研究をしています.どれくらいおおざっぱかというと,ドーナッツとマグカップの形が見分けられないくらいです(佐伯修教授の研究・技術カタログを参照).数学に限らず多くの学問は,対象を分類することを一つの目標としています.どんな性質に着目するかによって分類の基準が変わってきて,猫と犬というように大雑把に分けることもあれば,秋田犬と柴犬と言うように詳しく分類することもあります.トポロジーでは図形,より数学的にいうと空間を対象としますが,おなじみの合同や相似よりずっと荒く,連続的に変形できるものは区別しません.そんな”いいかげん”なことで役に立つのかと思われるかもしれませんが,実はさまざまな場面で活躍します.
まず,人間の視覚や空間把握は非常に大雑把ですが,多くの面でまだ機械を凌駕しています.細かな変化に気がつくのは苦手な反面,手書きの歪んだ文字や,笑顔でも泣き顔でも同一人物を認識することができます.また全く未知の図形,いわゆるビッグデータなどの高次元や時に無限次元の空間を扱う時,まずは大局的な情報が重要になります.新発見の島を調べるのに,いきなりルーペを持ち出してもあまり得るところはありません.それよりも高台に登っておおまかな形を知りたいでしょう.
もう一つ別の観点からは,柔らかい性質は適用範囲が広い,というのも利点に挙げられます.硬い性質を扱う数学的事実,例えば,球の体積の公式は,真に球なものにしか適用できませんが,世の中に存在するものはイデアからはかけ離れていて,常に誤差が生まれます.一方で,代表的な位相的性質である“穴の数”(正確にはベッチ数)は,歪んだ図形でも問題なく扱うことができます.
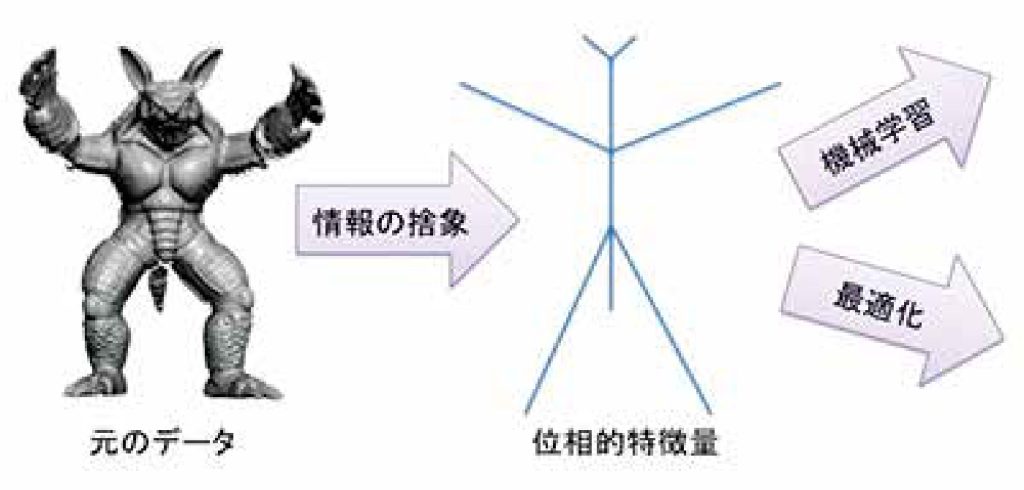
上にあげた特徴を眺めてみると,細かな差異に敏感な反面,全体像を捉える直感が働かないコンピューターと対極的に見えてきます.実際にトポロジーは,人間のもつ俯瞰的なものの見方を定式化し,コンピューターにその能力を授ける可能性を秘めています.
私は,空間のトポロジーを代数的に調べることに興味があります.主にリー群や等質空間といった対称性の高い空間の,位相不変量を定義・計算することを専門としています.また,代数はコンピューターの得意とする対象であり,応用として図形をコンピューターで処理するアルゴリズムの研究にも携わっています.一例として,下図にペンギン算をお見せします.形を代数化することで,異なった形状を足し合わせたり平均をとったりすることが可能になります.また様々な形の”地図”ができ(座標が導入され)ることで,どの形はどの形に似ているといった解析が可能になります.この考え方を応用して,コンピューターで形状をデザインする方法の開発や,医用画像・センサーデータの解析も行なっています.
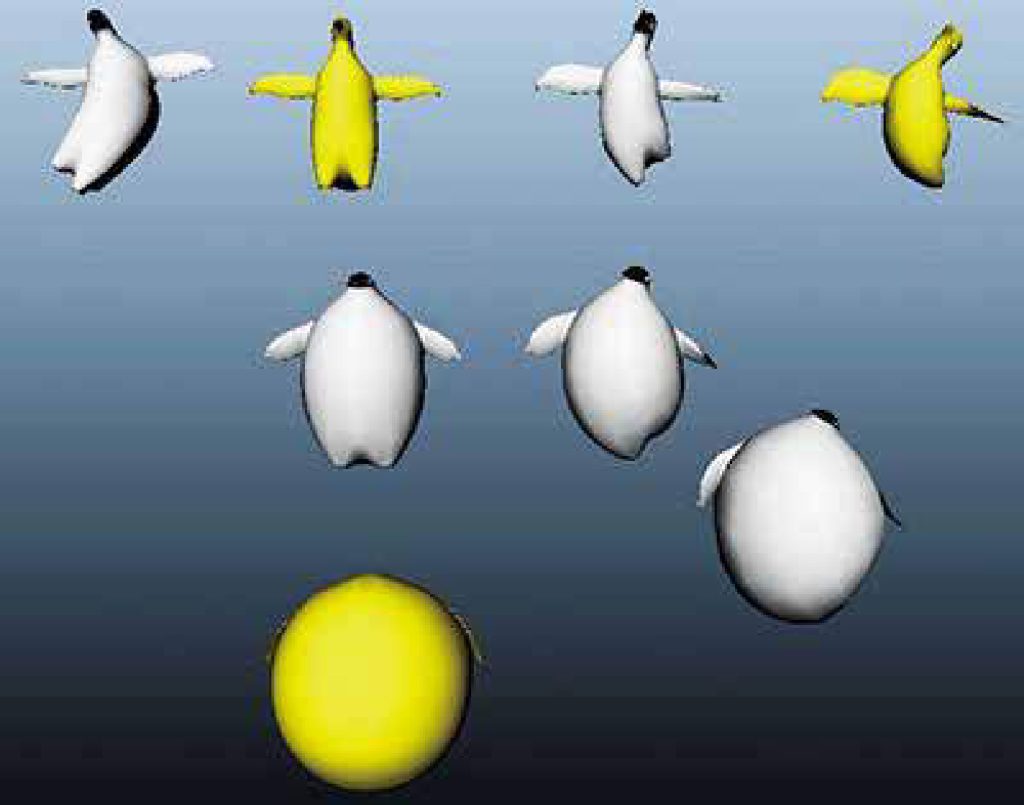
ペンギンのバリエーションを生み出す
物質構造解析の数理

富安(大石) 亮子
学位:博士(数理科学)(東京大学)
専門分野:応用代数・数論,数理結晶学,アルゴリズム
物質構造解析研究は,調和解析・信号処理・最適化・統計学など様々な手法を用いたアルゴリズム開発としての側面がありますが,私の場合,新しい知見を得るのに数論・代数学といった純粋数学のアイデア・技術を組み合わせることをよく行っています.
以下では,学術論文に加え特許出願に至った(したがって割と非数学者向けの)3つのプロジェクトを紹介します.
(1) 格子決定(Ab-initio indexing)に関わるCONOGRAPHの方法
”Ab-initio “とは専門用語で,物質構造(この場合は結晶格子)に関する事前情報を用いない解析のことです.以下の手法開発を行い結晶学分野でそれぞれ論文を書いた後,粉末回折用[1]・電子線後方回折用プログラム[2]を開発,web上で配布しています.開発には当時所属していたKEKの研究室,共同研究を実施していた(株)日本製鉄からの支援を受けました.
・ 大きな観測誤差下での格子対称性(ブラベー格子)の決定…格子基底簡約の応用
・ ピークサーチ
・ 実験データによくフィットする解の検出に用いるfigure of merit
・ 消滅則の一般的性質の導出(トポグラフを用いて記述)
・ 解析の解の一意性(Ambiguity)の高速判定法…数論の2次形式論の応用
開発したソフトウェアCONOGRAPHは解析の成功率を向上させました.得られた数学の結果は様々な回折データからの格子決定に対応できます.
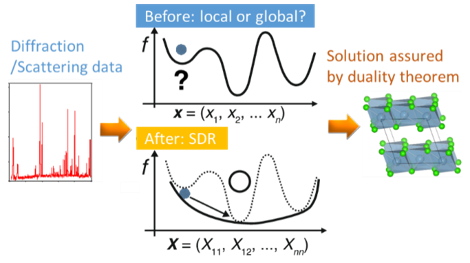
(2) 半正定値計画緩和法(SDR)に基づく結晶・磁気構造解析の方法
非線形最適化におけるローカルミニマムの問題はよく知られていまず.SDRは双対定理で保証された状況下において2次計画問題の大域的最適解を求める方法です.一般に,結晶構造のフーリエ変換すなわち「構造因子」の偏角を求める位相回復の問題(絶対値は観測値から得られる)は2次計画問題として表現できます.
もともと未知構造解析の解の一意性を調べるために始めた研究ですが,偶然,実験家との共同研究で役に立つ出口(磁気構造解析[3])も見つかりました.SDRの優れた性能は物質構造科学分野で代数計算・離散数学の応用を進めるためにも有用と考えています。
(3) 黄金角の方法の一般化・高次化
葉序・ひまわり頭部に見られるパターンのモデリングに使用される黄金角の方法の一般化は様々な文献で試みられ,取り上げられた未解決問題でしたが,マルコフ理論の高次元版であるproduct of linear formsと呼ばれる数の幾何・数論の問題に帰着させることで一般曲面・一般次元に適用可能となりました.
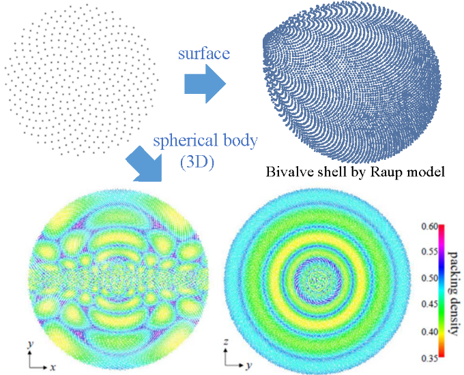
モデリング・パターン生成・メッシュ生成において今回開発した方法・理論の応用を展開する予定です.
[1] https://z-code.kek.jp/zrg/
[2] J. Appl. Cryst. (2021) 54 (2), 624-635
[3] Scientific Reports (2018) 8:16228.
Topological Data Analysis and Machine Learning

Keunsu KIM
学位:博士(数学)(POSTECH)
専門分野:Topological Data Analysis (TDA), Optimization problems in TDA
My primary research interest lies in the intersection of Topological Data Analysis (TDA) and Machine Learning (ML). In particular, I am currently focused on optimization problems in TDA.
Topology is the study of continuous objects, known as topological spaces, and the properties that remain invariant under continuous deformation. One of the most well-known invariants is homology, which quantifies the “holes” in a space and can be efficiently computed using linear algebra.
TDA can be applied to various types of data, including point clouds, time series, and images. Persistent homology is a central tool in TDA, which quantifies the connectedness, holes, and higher-dimensional structures present in the data. These topological features are summarized using a persistence barcode.
Figure 1 illustrates the core idea of this study in an intuitive manner using a Hangul image dataset. The characters shown in the figure—namely 가, 다, 라, 갸, 댜, 랴—are structurally composed of basic elements, namely consonants (ㄱ, ㄷ, ㄹ) and vowels (ㅏ, ㅑ). While humans naturally perceive these consonants and vowels as meaningful and fundamental decomposition units, applying a purely data-driven matrix factorization method, such as standard Nonnegative Matrix Factorization (NMF), often leads to undesirable results. In particular, the basis vectors learned by NMF may exhibit disconnected strokes, resulting in characters being represented as fragmented or semantically meaningless pieces. As shown in the red boxes in the NMF basis row of Figure 1, a single character appears as three mutually disconnected components. This structural fragmentation is directly reflected in the persistence barcode shown at the bottom of the figure. The short bars correspond to disconnected components, and their lengths can provide a quantifier of the degree of disconnectedness in the extracted basis. This example highlights how topological information can be used to characterize and quantify structural deficiencies in standard NMF, thereby motivating the introduction of topological regularization.
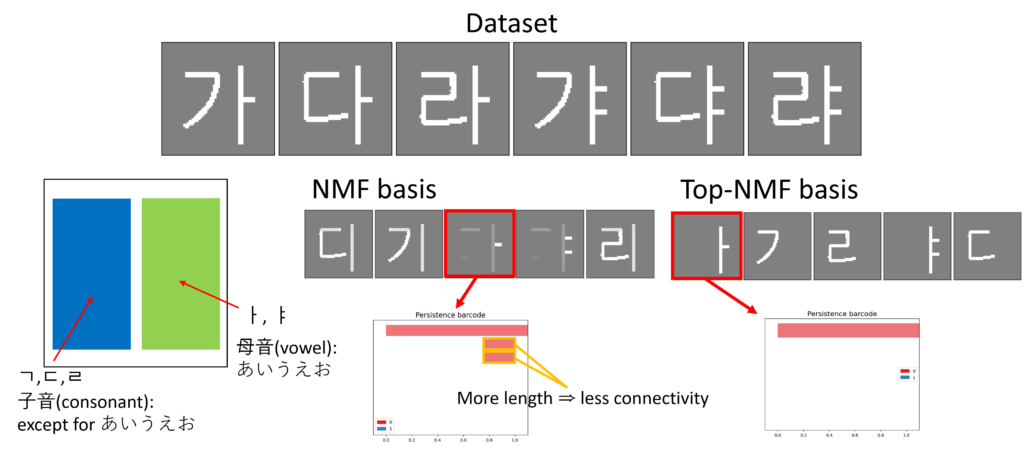
I am currently conducting research on optimization problems in TDA, with a particular focus on incorporating topological regularization the NMF (Top-NMF). By encouraging the decomposed components to exhibit topological properties such as connectivity and hole structures, we aim to derive semantically interpretable fundamental decomposition units.
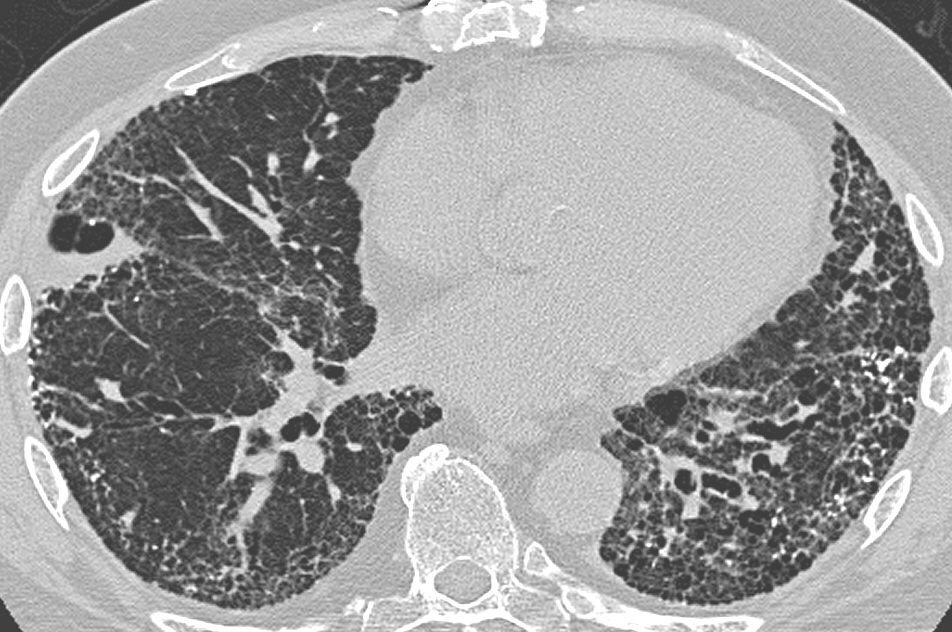
In addition, as a researcher participating in Moonshot Project 2, which focuses on ultra-early disease diagnosis, I am applying my theoretical framework to the analysis of medical imaging data. For example, certain lung diseases, such as honeycomb lung, exhibit characteristic topological structures in which holes appear within lung tissue, and, as illustrated in Figure 2. Building on the theoretical framework presented in Figure 1, future research aims to capture fundamental patterns observed in patients with lung diseases and to explore how this information can be utilized to support lung disease diagnosis.
L1正則化に基づくスパース多変量解析

廣瀬 慧
学位:博士(機能数理学)(九州大学)
専門分野:スパース推定,L1正則化,多変量解析
近年,ビッグデータ解析が重要視されていますが,データ量が多くなった反面,データの冗長性も増してしまい,必要のない情報を取り除いて有効な情報のみをうまく抽出することが必要とされています.それを実現する,極めて有効な方法の一つが,L1正則化法をはじめとする,スパース推定です.スパース推定とは,数万・数億にものぼる数のパラメータが存在するときに,ほとんどを「ゼロ」と推定することができる方法であり,非ゼロ要素に対応する変数のみが有効となります.この方法の良い所は,たとえ数万オーダーの次元のデータであっても,わずか数分で計算が完了してしまうくらいに高速なところです.計算効率が良い上に,統計的にも良い性質がたくさんあるため,L1正則化は多くの統計学者を魅了しているのではないかと思います.
私は,上記のL1正則化法を使った統計解析,とくに,多変量解析に興味を持っています.多変量解析とは,大量の変数があった時,似た変数をうまくまとめたりすることにより,変数間の関係性を見出す方法です.この方法は,古くから現在までずっと使われ続けている基本的な手法です.私は,多変量解析の中でも,因子分析と呼ばれる手法に興味を持っています.因子分析は,もともと心理学者が作った方法なのですが,近年は生命科学でも使われています.また,因子分析を拡張したテンソル分解は,機械学習の分野で使われ始めています.因子モデルの研究は今後ますます発展していくと考えられます.以下,私の最近行った2つの研究を紹介します.
(1) 因子分析のスパース推定
因子分析の面白い点は,モデルそのものに識別性がないというところです.このような解が一意に存在しないモデルは,統計学者からすると「奇異なモデル」となります.実際にどのようにパラメータを推定するかというと,因子回転と呼ばれる,因子分析独自の最適化問題を解きます.このような問題設定自体,他のモデルにはない独特なものですが,それが50年以上も使われてきたスタンダーダードな方法です.
私は,この因子分析モデルにL1正則化を適用すると何が起こるかを考えてみました.すると,正則化法が,因子回転の一般化であり,更に因子回転よりもスパースな解が得られるということを理論的に示すことができました.私はこの関係性を見出しただけでなく,パラメータをある程度高速に推定できるアルゴリズムを考え,さらにソフトウェアパッケージfanc(https://cran.r-project.org/web/packages/fanc/index.html)を作りました.実際にこのパッケージを使った論文もいくつかあります.
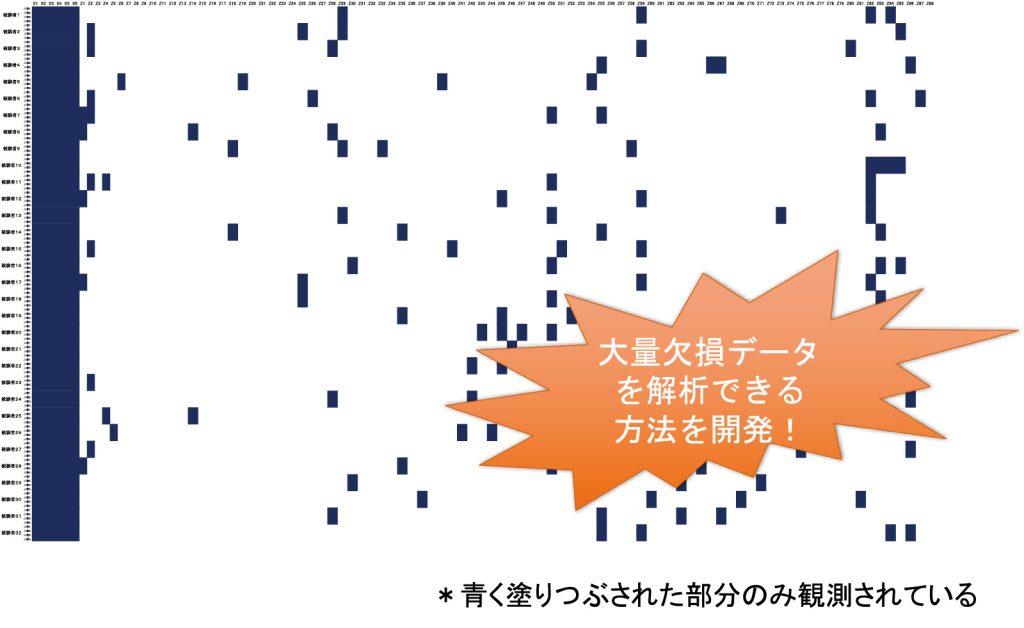
(2) データが大量に欠損する場合の因子分析モデルの最尤推定
NTTと共同研究している際,データに大量の欠損がある場合の因子分析をしなければならないということがありました(図参照).具体的には,アンケートを行う際,すべてのアンケート項目に答えるのでなく,その中のごく一部を選び,その選んだ項目のみ回答するというデータの取り方をしました.
データが欠損する場合,パラメータはEMアルゴリズムによって推定できますが,欠損数が多い場合,通常のEMアルゴリズムだと計算時間がかかってしまいます.そこで私は,大量欠損時の因子分析モデルにおけるEMアルゴリズムを提案しました.このアルゴリズムは,従来のEMアルゴリズムよりも,数百倍,場合によっては数千倍もスピードが早い事がわかりました.
Finite mixture models for statistical inference

Hien Duy NGUYEN
学位:PhD, University of Queensland, Australia
専門分野:Mathematical Statistics, Statistical Computing, Statistical Learning, Bayesian Statistics, Signal Processing, Stochastic Programming, Optimization Theory
Many real-world datasets are heterogeneous and multipopulational phenomena. In such contexts, it is insufficient to capture the overall variation among the data using a single statistical model. Therefore, a cohesive approach to modeling the multiple subpopulations within the superpopulation is necessary. In such scenarios, a useful approach involves modeling each subpopulation and their contributions to the superpopulation through a weighted averaging construction, known as a finite mixture model. These models are highly flexible and interpretable, enabling them to capture and provide inference for known heterogeneities in the data while also identifying new heterogeneous phenomena that were previously concealed.
The class of finite mixture models is extensive, and choosing between different mixture models can be challenging. In my work, I have studied model selection procedures required to make mathematically principled choices among competing finite mixture models. I have made progress in two key directions to address this problem. Firstly, I employ sequences of hypothesis tests to determine the number of components or subpopulations required in each mixture model. This approach relies on a new hypothesis testing method called universal inference, which offers a straightforward and assumption-light mechanism for deciding whether a model accurately represents the observed data. Using these universal inference tests, I have developed a way to construct confidence intervals for the number of underlying subpopulations in the data, providing insight into the complexity of the overall superpopulation.
Secondly, by leveraging modern stochastic programming techniques for optimizing random objects, I have developed new penalization methods for selecting between different finite mixture models within broader model selection and decision problems. My novel information criterion, known as PanIC, offers a more assumption-light alternative to existing methods like the Bayesian information criterion or Akaike information criterion. PanIC provides a single-number summary for choosing between competing models, guaranteed to asymptotically select the correct model as the dataset size increases.
Beyond their utility for modeling heterogeneous processes, finite mixtures and their regression variants, the mixture of experts (MoEs) also serve as excellent functional approximations of probability density functions (PDFs) and conditional PDFs that characterize statistical relationships. My colleagues and I have contributed to understanding the approximation theoretic properties of mixture models and MoEs for various classes of PDFs. We have provided sufficient conditions for ensuring that PDFs, conditional PDFs, or mean functions of conditional PDFs can be effectively approximated using a sufficiently large number of components in a finite mixture model construction. These results, often referred to as universal approximation theorems, are valuable for determining whether a class of functions serves as an adequate basis for modeling an underlying mathematical phenomenon.
My research in mixture model computation, estimation, and inference has found widespread application in real-world scenarios. For example, I have collaborated with neuroscientists and cell biologists to analyze heterogeneous biological phenomena, worked with quantum physicists to characterize switching behaviors of quantum circuitry, assisted economists in characterizing subpopulations of experimental outcomes, partnered with civil engineers to study regional differences in traffic behavior, supported fisheries scientists in characterizing growth stages of aquatic species, and collaborated with image scientists to segment and characterize imaging data, among other practical applications.
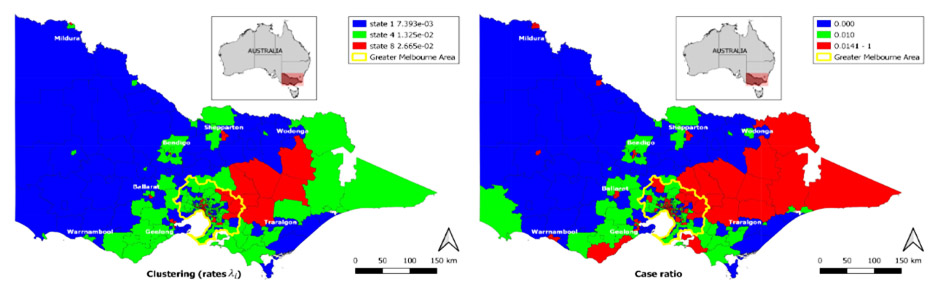
Figure 1: Traffic crash rate clustering of different regions in Victoria, Australia.

Figure 2: Quantization of mandrill photograph using different mixture models.
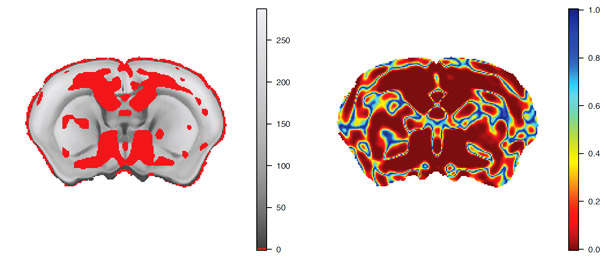
Figure 3: Mixture-based false discovery rate control of p-values for a mouse brain morphometry experiment.
ベイズ推定による計測と数理モデリングの橋渡し

徳田 悟
学位:博士(科学)(東京大学)
専門分野:ベイズ推定、モデリング、情報統計力学
古くは17世紀に発見されたケプラーの法則が象徴するように、単純な数式を用いて計測データを表す数理モデリングは様々な物理現象に対する理解を深めてきました。しかし、扱う現象が複雑になり、高度な計測技術を駆使する現代科学では理解が困難な計測データが顕在化しています。私は計測データに根ざしたモデリング原理を確立し、あらゆる現象を曖昧さなく理解する指針を打ち出す研究に挑んでいます。特にベイズ推定という統計的手法の数理を探求するとともに、凝縮系物理学を始め、広く自然科学の研究者との異分野協働による実証研究を推進しています。これまでの研究を通じて、私は理解が困難なデータの要因となり得る次の三課題に着目しています。
(1) モデルの不定性
モデルは現象の本質を表しますが、何が本質かは常に自明ではありません。多くの場合、その判断は研究者の洞察に委ねられ、時に研究者間で見解の相違が生じています。例えば図1の計測データが示す振動現象は摩擦が無視できれば単振動、そうでなければ減衰振動を表す関数によってモデリングできますが、どちらが妥当かは場合によります。
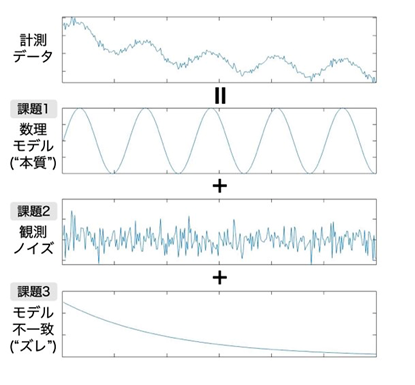
観測ノイズとモデル不一致の具体例
我々は計測データに対するモデルの妥当性を
確率として定量化するベイズ推定を用いて、こうした不定性を解消する実証研究を進めています。実際、速度分布関数やバンド構造といった凝縮系物理学のモデルの選択において有用性を示してきました。
(2) 観測ノイズの存在
データの計測には必ず観測ノイズを伴い、観測ノイズが大きいほど、データから推定するパラメータの値も不確実になります。我々はこのような誤差伝搬の性質がモデルの評価にも影響することに着目し、ノイズの強度と妥当なモデルを同時推定する方法論を開発しました。また、実証研究を通じてその有用性を示しました。パラメータの値やモデルの推定はノイズの強度(データの質)とデータ量に依存します。我々はベイズ推定と統計力学の数学的な対応(情報統計力学)に立脚し、理論解析を進めることで、ベイズ推定に対する計測データの量や質のスケーリング則を解明しました。
(3) モデル不一致の存在
理想と現実、つまりモデルと計測データの間には必ずズレがあります。まず、モデルは真実の近似表現です。また、真実とデータの間には観測ノイズや系統誤差が生じます。私はこれらの内、ランダムなノイズ以外をまとめてモデル不一致と総称しています。モデル不一致の起源を帰属することは容易でなく、それらを具体的な数式で記述することはさらに困難です。加えて、ベイズ推定に正当性を与える従来の漸近理論はモデル不一致がない理想的な状況を仮定するものです。我々は実証研究を通じ、モデル不一致を系統的に対処する方法論を開発するとともに、その正当性を裏付ける新たなベイズ推定の漸近理論の構築を進めています。
小区分別統計的推測法の理論発展及びその活用

廣瀬 雅代
学位:博士(工学)(大阪大学)
専門分野:統計科学,小地域推定,混合効果モデル
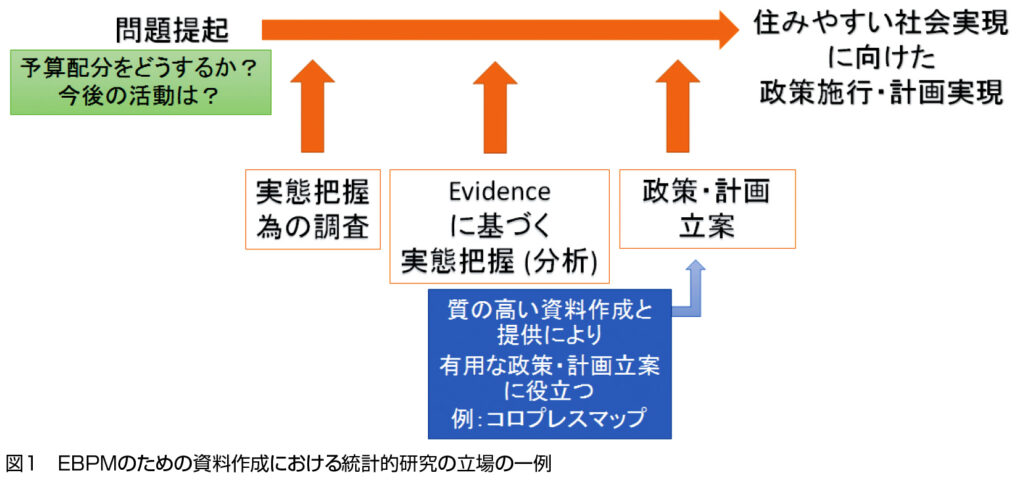
データサイエンス全盛のこの時代に,Evidence Based Policy Making (EBPM)の重要性が認識されつつある.その中で小区分ごとの実態把握に基づくより丁寧な計画立案への期待も大きくなっており,調査データによって小区分ごとの特性値を推定する際,区分ごとの情報のみならず,統計的モデルを介して他の区分からの情報を有効に活用することで,統計的精度向上の達成が期待できる場合がある.
そのため,このような統計的推定手法を活用したエビデンス資料作成・提供は,有用な計画立案の礎になり,社会的課題解決への期待を高めることができると考えている(図1参照).
統計的モデルを用いたモデルに基づくアプローチの研究は,海外の官庁統計分野でも盛んに行われ発展を遂げている.官庁分野のみならず,他の様々な応用分野で重要視されている研究でもある.ここで,モデルに基づくアプローチに関する私の研究内容を2つ簡単に紹介する.
(1)小区分別統計的推測法の理論
小区分ごとに特性値を推定する場合,統計的モデルを活用したモデルに基づくアプローチでは,仮定モデル下の線形不偏なクラスの中で平均二乗(予測)誤差を最小化する最良線形不偏予測量に対する経験的最良線形不偏予測量が多くの場面で活用される.しかし,従来用いられる方法は実用面からの問題を複数抱えている.私は,その経験的最良線形不偏予測量とその予測誤差の問題を考慮に入れた,統計的精度の損失がほとんどない,改善可能性のある手法の開発を目指している.また,リサンプリング法と同様の統計的精度を保ちながら,計算負荷を軽減できる,より実用的な経験的ベイズ信頼区間法の提案も行っており,さらなる効率的な統計的手法開発とその理論保証に取り組んでいる.
(2)実データ分析への応用
開発した統計的手法を実データに適用し,質の良いエビデンス資料作成に取り組んでいる.これまでにも,過去に開発した統計的推定手法を,わが国のある都市住民を対象とした意識調査データに適用し,小区分別に防災意識レベルの実態把握を図っている.さらに,国勢調査小地域集計との共通項目データを活用して,国勢調査結果との誤差を調べている.その結果,(国勢調査小地域集計を真とした場合,)慣習的に用いられてきた推定手法と比べたときの適用手法の一種の有用性を示すことに成功している.詳細は廣瀬ら(2018,日本統計学会誌)を参照されたい.
統計的ダイバージェンスに基づく頑健なモデル選択規準

倉田 澄人
学位:博士(理学) (大阪大学)
専門分野:数理統計学、モデル選択、ロバストネス
例えば突出した能力、例えば災害級の現象、例えば観測機器の故障、例えば人的なミス…等々、現実のデータには様々な由来を持った、他の観測値から見て大きく外れた値を取るデータが付き物です。これを「外れ値」と呼びます。この外れ値ですが、何を以て外れ値とするか、どこまでが外れ値でなくどこからが外れ値であるかという明確な定義、線引きは与え難いものです。また、災害やミスを完全に零にするということが非常に難しいため、外れ値の発生を防ぐことは事実上不可能と言わざるを得ません。その為、外れ値が混ざっていてもその影響を小さく抑えられる「頑健(ロバスト)」な分析手法が、分析において重要な意味を持つと考えられます。私は、モデル選択問題を中心に、頑健な手法について研究を行っています。モデル選択規準は、自然現象や人間の行動を表現する数理モデルの候補の中から最も好ましいモデルを択ぶ尺度です。私はこれまで特に、確率分布間の遠さを測る「統計的ダイバージェンス」を用いて、現象や行動の根底に在ると考えられる「真の分布」とモデルとの近さを測るという観点から導出されるモデル選択規準を検討してきました。モデル選択問題を考えるにあたっても、頑健性は重要な性質と言えるでしょう。しかし、従来広く用いられている、Kullback-Leiblerダイバージェンスに基づいたモデル選択規準は、データに外れ値が混ざっていると選択精度を落としてしまう傾向にあることが指摘されています。そこで本研究では、統計的推測において頑健性に優れることが知られている、「BHHJダイバージェンス」と呼ばれるダイバージェンスに基づいて、従来のAICやBICを拡張したモデル選択規準を導出し、検討してきました。
外れ値は頻繁に、パラメータ推定やモデル選択へ悪影響を及ぼします。モデル選択における頑健性を議論する為には、モデル選択規準の値の、外れ値によって生じる変動を評価する必要があると考えられます。本分野ではしばしば、データを発生させている分布に外れ値が含まれている場合といない場合との差を評価することで、外れ値の混合に対する敏感さを評価します。観測値の大部分は「真の分布」から発生していると想定し、そして外れ値は「真の分布」とは別の分布から出現しているものだと解釈します(図1)。私はこれまで、多くのダイバージェンスに基づいたモデル選択規準の頑健性を比較検討してきました。結果として、BHHJダイバージェンスを筆頭に、幾つかのダイバージェンスに基づいた規準の頑健性が分かってきました(図2)。あらゆる現象に対してモデルが作成出来る以上、良きモデル選択規準を検討することは、あらゆる分野に対して意義を持ちます。頑健性をはじめ、選択に資する様々な性質を詳しく調べることで、文理を問わず幅広い分野を支えられる研究を目指しています。
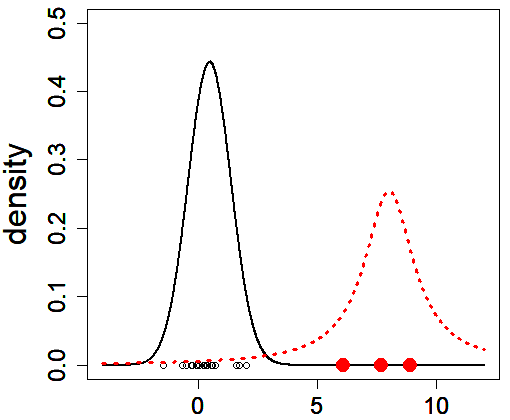
(図1) 一つは黒い線で画かれた「真の分布」、もう一つは赤い線の外れ値を発生させる分布、これらの異なる確率分布を考え、観測値はこの二つの分布の混合から発生していると想定します。もし、黒の分布のみからデータが出てきているときと、混合分布から出てきているときで分析結果が大きく異なれば、その手法は外れ値に対して敏感(頑健ではない)と考えることが出来ます。
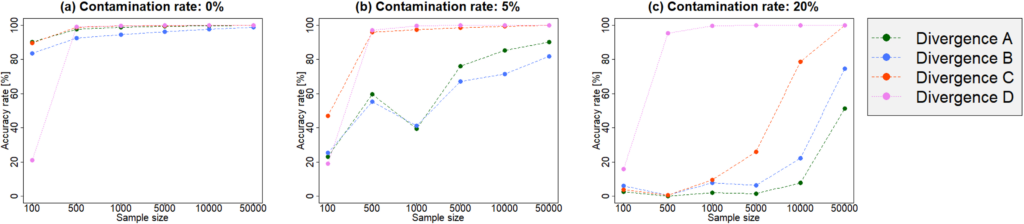
(図2) 一般化線形モデルの数値シミュレーションにおける、幾つかのダイバージェンス(Divergence A-D)に基づいたモデル選択規準のaccuracy rate (正しいモデルを選択した率)です。三つのグラフは異なる外れ値の混合率(0%、5%、20%)に対応しており、それぞれの横軸はサンプルサイズ(観測データの個数)を指します。Divergence AとBに基づく規準は外れ値があると精度が大きく下がっており、混合による悪影響を敏感に受けていることが分かります。一方でDivergence Dの規準は、全ての混合率に対してほぼ同じaccuracy rateになっており、強い頑健性が見て取れます。
数学と暗号の交差点

縫田 光司
学位:博士(数理科学)(東京大学)
専門分野:暗号数理,秘密計算,組合せ論的群論
インターネット経由での安全な買い物など,現代の便利な生活の基盤となっている情報技術のさらに基盤となっている技術の一つが暗号技術です.さらにその暗号技術の基盤として数学が役立っています.1970年代後半に考案されたRSA暗号では初等整数論が,1980年代半ばに考案された楕円曲線暗号では名称の通り楕円曲線の性質が活用されています.さらに,来たるべき量子コンピュータ時代に備える次世代暗号(耐量子計算機暗号)には,線型代数やグレブナー基底や高次元整数格子などまた別のさまざまな数学が現れます.
数学者の目線で暗号分野を眺めたとき,「より新しく多彩な数学を実戦投入する」楽しさはもちろんのこと,それ以外に「素朴な数学的道具でも,使い方次第で大きく花開く」という楽しさや,「安全性」など暗号分野の様々な概念に対して「より直感に沿った,かつ理論的にもより取り扱いやすい「良い」定義を探究する」といった楽しさも感じられます.
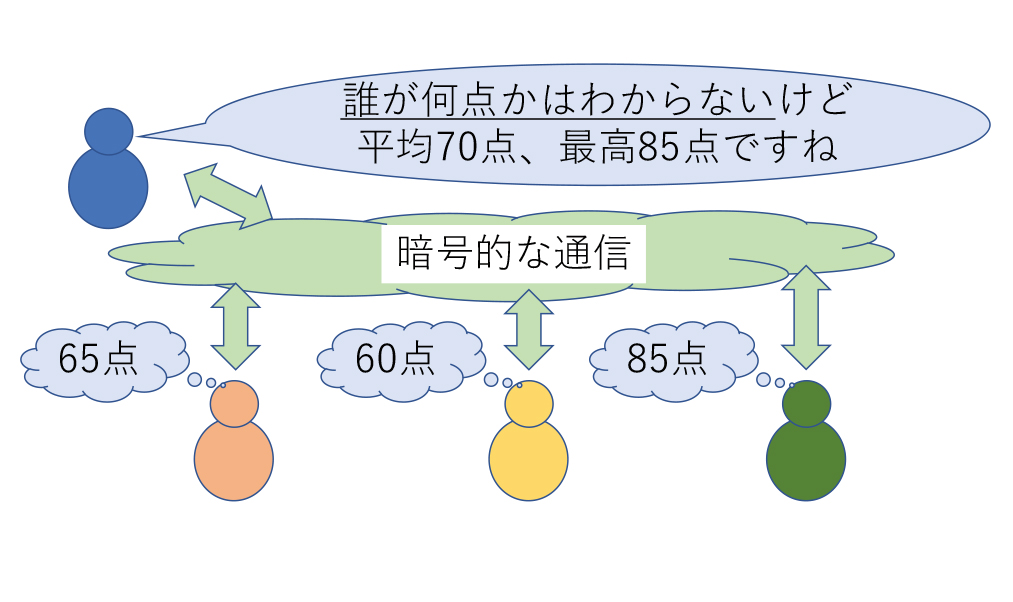
暗号分野で私が近年主に取り組んでいる研究テーマは「秘密計算」と呼ばれる技術です.秘密計算は,複数人がデータを持ち寄って行う情報処理において,「データを互いに見せない」のに「欲しい計算結果はちゃんと得られる」という手品のような性質を実現する暗号技術です.秘密計算によく用いられる数学的・暗号的な道具のうち,「完全準同型暗号」という技術は,暗号化したままの状態で暗号文の中身のデータに対する計算を行える特殊な暗号化技術です.私たちの論文(国際会議EUROCRYPT 2015で発表)で構成した完全準同型暗号では「有限体上の関数はどれも多項式で表示できる」という性質が要となりました.この性質自体は代数学の初歩的な内容なのですが,それを「上手いタイミングで使う」ことで暗号学的に有意義な成果が得られたという実例となっています.
この完全準同型暗号については,既存の構成手法においてどうしても外すことのできない複雑な操作が存在し,効率化の妨げとなっています.私の最近の研究では,従来研究で用いられていなかった群論的な手法を用いてこの複雑な操作を回避することを目指しています.この研究には,数学における私の専門である組合せ論的群論の知見も活用できると見込んでおり,その意味でもやりがいのある研究です.
他にも秘密計算に関する最近の研究として,従来この分野で安全と考えられてきた「直感的にもっともらしいある種の構成法」が実は安全でない場合があることを示す「病的な反例」を発見しています(国際会議PKC 2021で発表).これもある意味で「いかにも数学者的」な研究でしょう.
これらの事例に限らず,暗号分野には(他の応用分野でもそうでしょうが)本当に多種多様な数学が関わっていて,私自身の研究でも「まさかこんな数学が役に立つとは」と驚いたことが何度もありました.そうした数学と暗号との豊かな関連性についての情報発信もより一層進めていきたいと思っています.
耐量子暗号の安全性解析

池松 泰彦
学位:博士(数理学)九州大学
専門分野:耐量子暗号,多変数多項式暗号
現代の情報セキュリティを支えるRSA暗号・楕円曲線暗号は,素因数分解問題・離散対数問題などの計算困難数学問題を安全性の根拠として構成されます.しかし,大規模な量子コンピュータが将来的に開発されると,Shorの量子アルゴリズムにより,素因数分解問題・離散対数問題などは多項式時間で解読でき,結果として,RSA暗号などは安全でなくなることが知られています.
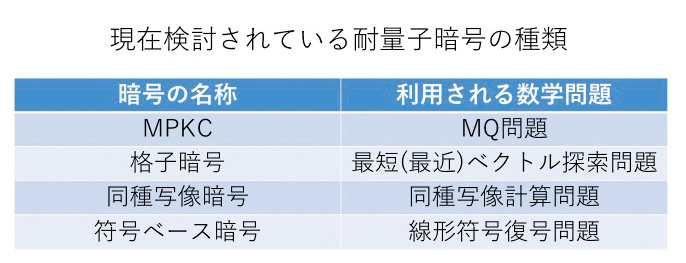
量子コンピュータでも解読困難とされる暗号(耐量子暗号)は,上記のような背景から,現在世界中で活発に研究開発が行われています.この研究には,素因数分解問題・離散対数問題とは異なる数学問題が扱われ,広範囲な数学理論が必要となります.

私は,耐量子暗号の中でも,特に多変数多項式理論を用いた,多変数多項式暗号(MPKC)に興味を持ち,研究を行なっています.MPKCは,有限体上の多変数二次連立方程式の求解問題(MQ問題)の困難性を安全性の根拠として構成されます.このMQ問題はNP完全問題であることが証明されており,そのことから,量子コンピュータでも解読困難な暗号が構成できると期待されています.
MPKCは,その他の耐量子暗号(格子暗号や同種写像暗号など)と比べても高速な処理性能を有し,さらに署名方式においては署名長が最も短くなることから,IoTで取り扱う機器やICカードのような低資源デバイスでの実装に向いていると考えられています.また最近では,署名方式の一つであるRainbowから仮想通貨を作るという面白い試みも行われています.
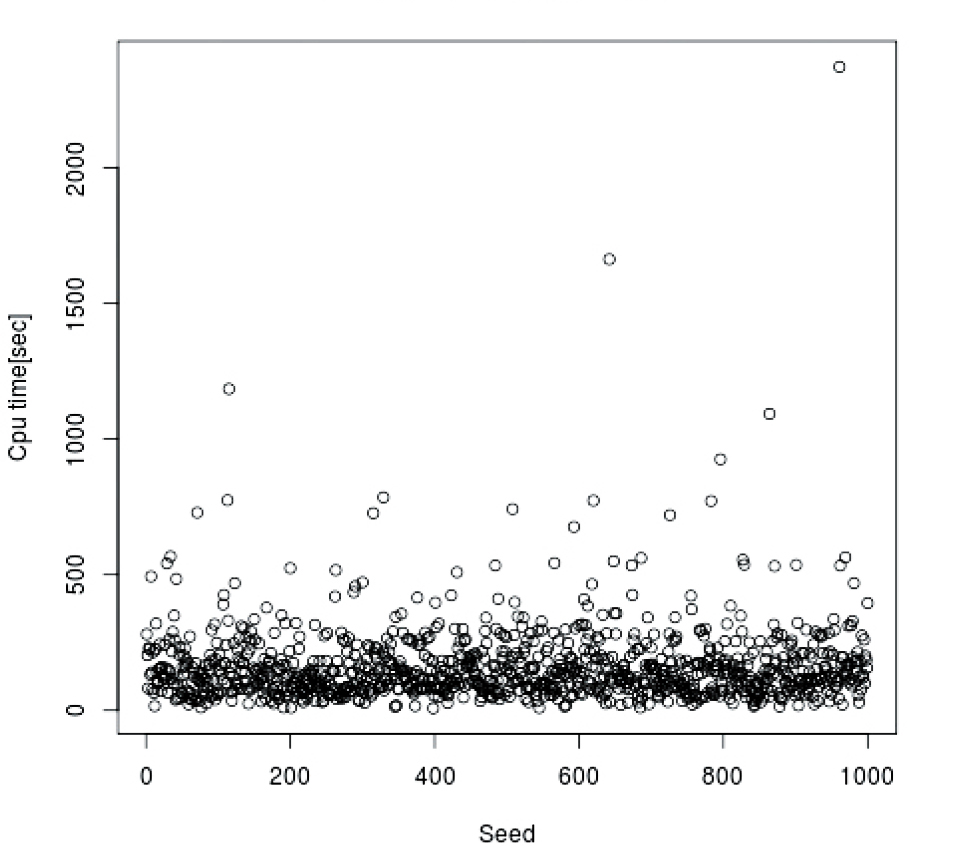
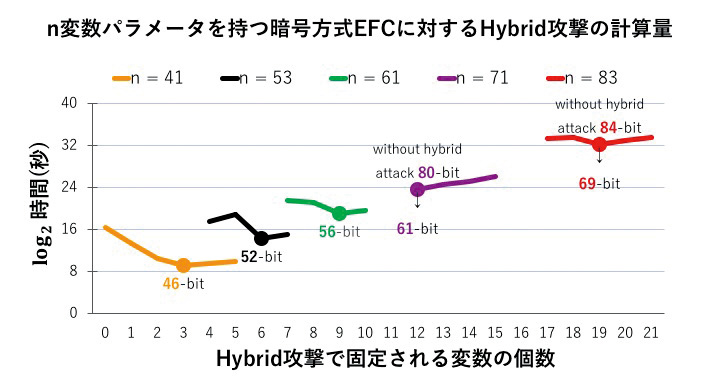
私は,主にMPKCの安全性解析について研究を行なっています.それには,グレブナー基底や代数幾何などによる数学的議論が欠かせません.しかし,グレブナー基底アルゴリズム,特にF4/F5アルゴリズムによる攻撃計算量の解析は,理論的にはまだまだ未解明であり,実験による解析に基づいています.私が現在研究している暗号方式EFCにおいても,Hybrid攻撃を用いることで,安全性が想定されていたものより低下することを実験的に示しましたが(下図),それらを理論的に説明することが未解決であり,今後の研究課題となっています.
またMPKC以外にも格子暗号や同種写像暗号についても研究を行なっており,これらを組み合わせた新しい耐量子暗号の開発にも関心があります.
「変な振る舞い」=「素直な振る舞い」

松江 要
学位:博士(理学)(京都大学)
専門分野:力学系、数値解析、精度保証付き数値計算、特異摂動論、燃焼など
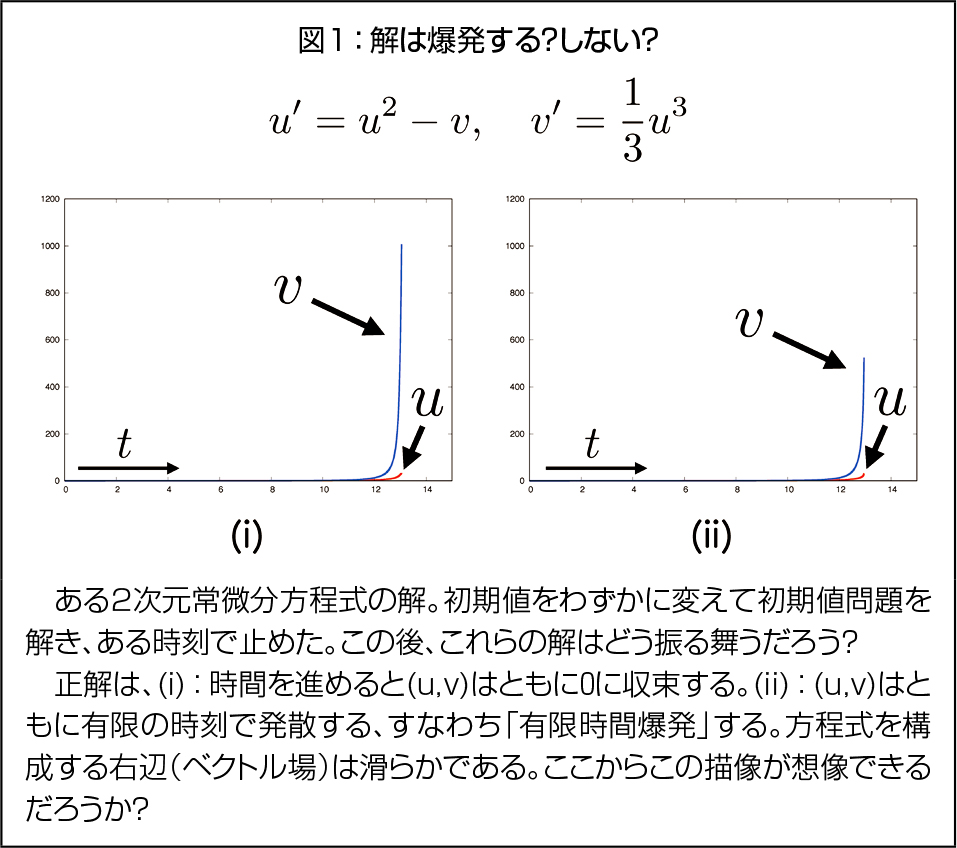
物体の動き、空気の流れ、物体や空間の温度など、多くの自然現象は微分方程式の解で記述されます。典型的に、解は徐々に(定数や時間周期的な振動する関数などで記述される)一定の状態に近づく、あるいは指数関数的に発散しますが、時折この枠組みに当てはまらない「特異」な動きをするものがあります。例えば u’ = u2 (’は時間微分)について、時刻t=0におけるuの値を正の値に取ると、解はある有限の値Tに対して、t→Tの時に無限大に発散し、それ以降方程式は「解けなく」なります。
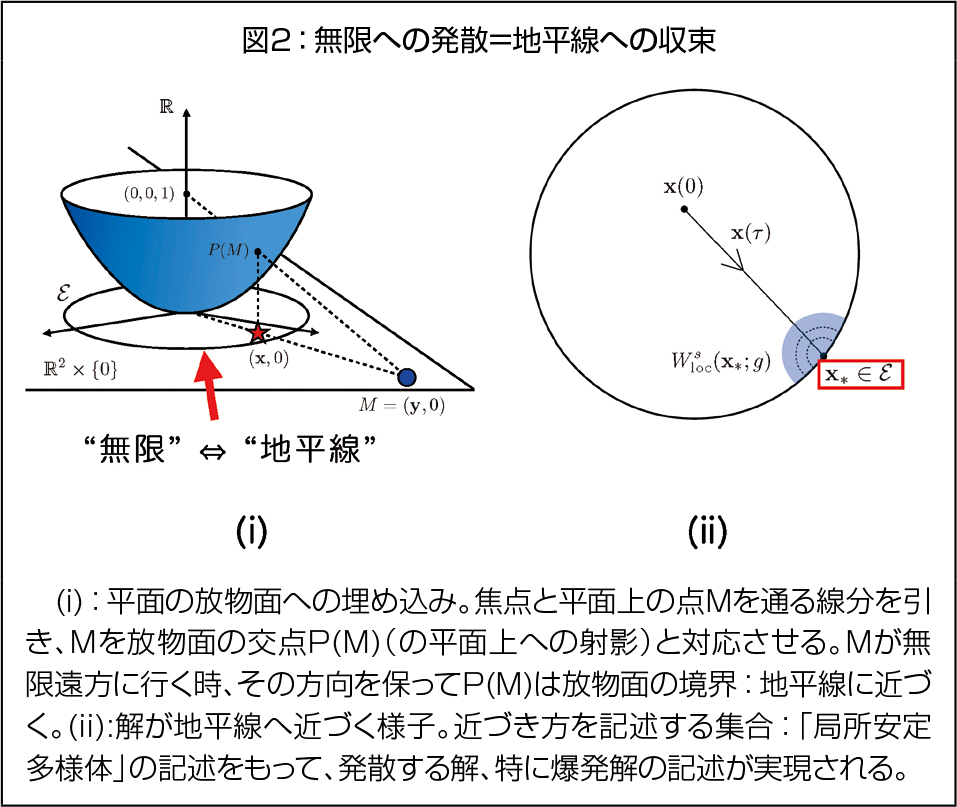
これは典型的な物理現象では起こり得ない「変」な振る舞いで、解が「有限時間爆発」すると言います。有限時間爆発は熱源着火に付随する熱暴走、連鎖的化学反応による反応暴走、エネルギー集中に伴う極短時間における梁の急激・爆発的な振動など、特異な現象の数学的対象物としてしばしば確認されます。一方、上の方程式が示すように「系=現象の支配法則」自体は特異性がない場合も多く、与えられた系に対して「爆発は起こるのか」、起こるとすれば「いつ、どこで、どのように」起こるのかは非自明な問いであり、このような振る舞いを制御するには現象そのものの理解を深める必要があります。他方、爆発現象の場合は「無限大」あるいは「無限遠」を直接相手にするため、数学的にも数値的にも捉えることが難しく、この現象そのものが長年の数学的な研究対象とされています(図1参照)。
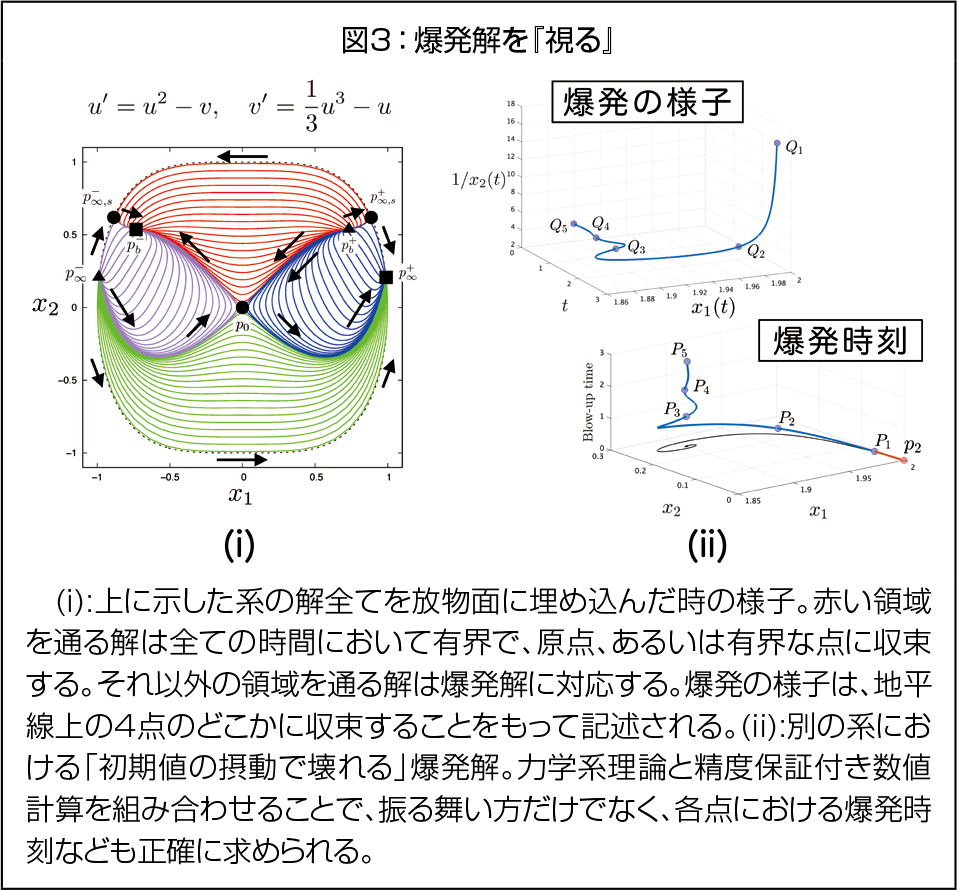
ここで私は、「無限遠」など変・特異な振る舞いを誘発する因子の捉え方を変えることで、物体の動きや温度と同じように「素直」に爆発現象などの「変な振る舞い」を捉え、統一的記述を実現することを研究テーマの1つとしています。具体的な1つのアイデアは「空間全体を半球面やカットされた放物面の中に埋め込み、その境界として無限遠を表現する」というものです。複素関数論におけるリーマン球面、位相空間論におけるコンパクト化に類するものですが、ここでは系の持つスケール性にも着目し、適切な(境界つき)曲面への全空間の埋め込みを構成し、その境界:「地平線」として無限遠を表現します。この考え方自体は代数幾何学などで見られる特異点や無限遠点の捉え方に端を発するものですが、全ての解のとり得る(定性的な)振る舞いを包括的に記述する力学系理論と組み合わせることで、「無限大に発散する解=地平線上の集合に収束する解」という対応を得られます。さらに、地平線への収束の仕方から、変換する前の解の爆発の様子を正確に記述することも可能になります。これは力学系理論の幾何学的側面、代数幾何学由来の系の適切な変換、漸近解析を組み合わせて実現されるものです。
このアプローチの利点の1つとして、数値計算・数値解析など、他の理論や技術との親和性が非常に高いことが挙げられます。(1):爆発の有無を含めた解の振る舞いを網羅する、(2):初期値の摂動で壊れてしまう爆発解を、数学的厳密性をもって数値計算する、(3):「複雑」な爆発の様子も地平線の様子で正確にわかる、などです。これらは精度保証付き数値計算、特異点論などを組み合わせることで実現できます。
解の爆発だけでなく、時間に付随して起こる様々な変な振る舞い:「有限時間特異性」は捉え所が難しいものです。しかし、上記のように見方を変えることで、実は別な角度から見た素直な振る舞いに過ぎないことが徐々に明らかになっています。この考え方は、古くはマルチスケールダイナミクス、最近では転換点(Tipping point)なども、力学系理論や幾何学の知識で「素直な解釈」が可能となっています。これらを包括的に記述する思想は、様々な点で「変なもの」=「素直なもの」という見方を得ることに繋がるでしょう。
波形パターンによる説明可能なAI

山口 晃広
学位:博士(情報科学)(名古屋大学)
専門分野:機械学習, XAI, 時系列データマイニング, 解釈性
私の専門分野は,説明可能な機械学習や時系列データマイニングです.インフラ・製造分野向けに,センサデータを用いたAIによる高信頼で効率的な設備診断を目指しています.この産業分野では,AIの判定性能以外にも,次のような課題がよく現れます.
課題A) → 現場の専門家は,波形に専門知識を持ち,AIの判定根拠を知りたい.
課題B) → 設備や製造装置は殆ど正常に稼働しており,異常事例の収集が難しい.
このような産業課題に対応するため,AIの判定に用いる波形パターンを発見する機械学習技術を提案し,事業適用を進めています.以降では2つのアプローチを紹介しますが,専門分野に限らず数理技術と事業課題を結び付けることも目指しています.
(1)Shapelets学習
データマイニングや機械学習の分野で,正常や異常などのクラスに属する時系列データセットを入力して,新しい時系列データのクラスを自動判定するクラス分類が研究されています.その中で,クラス分類に用いる局所的な波形パターン(shapelets)も分類モデルと一緒に学習する技術があります.この技術では,shapeletsの個数 K や長さ L を事前に与えるとその形Sは K×L の行列となり,クラスの誤分類を最小にするようにSを求める連続最適化問題として定式化されます.この技術を用いると,専門家はねじの緩みなど故障に関係する機械的な現象とshapeletsを照合して判定根拠を解釈できます.そのため課題Aを解決します.
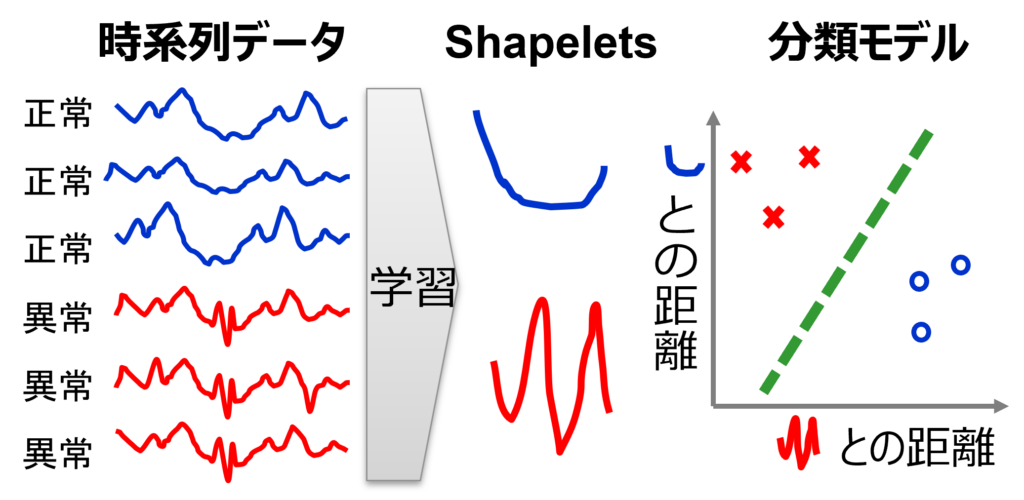
分類に用いる局所波形パターン(shapelets)の学習
しかし,従来技術では学習時に異常事例も必要となり課題Bを解決しません.そこで,課題A&Bを解決するため,正常事例のみでshapeletsを学習する異常検知技術を開発し,変電所設備に適用しました.正常なshapeletsから波形が最も崩れた箇所を拡大すると,異常兆候波形の傾きが僅かに緩やかであることが分かり,部品の不具合で設備の動作が緩慢になるという専門家の知見と一致しました.このように,専門家は判定根拠に納得しAIを利用できます.
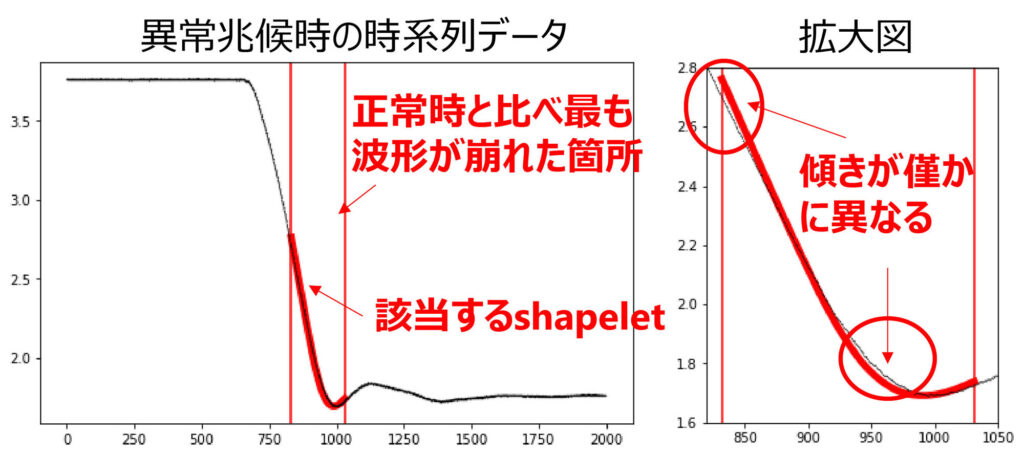
変電所設備へ適用した際のshapelets学習の判定根拠
(2)反事実波形生成
判定根拠を提示せずに高い分類性能を達成する技術が現れ,インフラ・製造分野でも高い異常検知性能を確認しました.そこで,判定部と根拠提示部を切り離し,それぞれで高性能化をはかる説明可能AI(XAI)に着目しています.その中で,反事実説明という方法を適用すると,shapelets学習のように,分類や異常検知の判定根拠となる局所波形パターンを生成できます.変電所設備の動作終了時に衝撃を吸収するタイミングがずれるという種類の異常に,開発した本技術を適用し,適切な反事実波形が生成されることを専門家と確認しました.
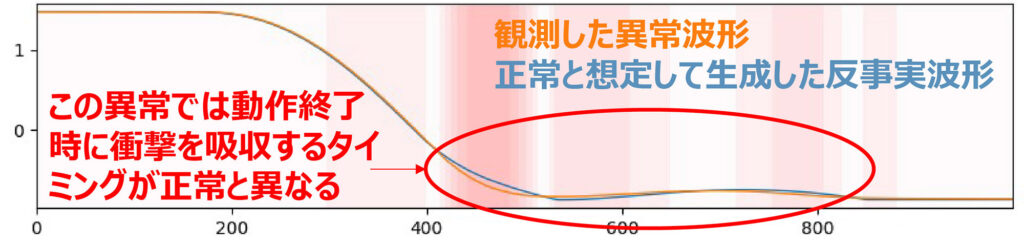
反事実波形生成による判定根拠
ソーシャル数理と動的最適化

吉良 知文
学位:博士(機能数理学)(九州大学)
専門分野:ソーシャル数理,動的最適化,確率最適化,マルコフ決定過程
私の専門分野は数理最適化です.特に,意思決定が繰り返し必要な問題(多段意思決定過程)や不確実性を含む問題(確率モデル)に関心があります.私は,この種の問題を効率良く解決する手法である動的計画法の理論とその応用の研究に従事してきました.また,社会的課題に対して,数理技術(最適化やゲーム理論など)を用いて,公平で納得度の高い制度や施策を設計する研究(ソーシャル数理)に従事しています.これまで社会的課題の現場と協働して技術開発をおこなってきました.以下では,2つの事例を紹介します.
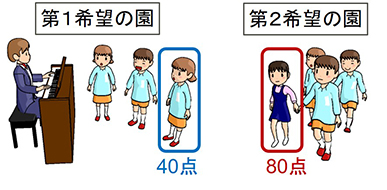
保育所の利用調整(選考)では,申請者の優先順位(保育の必要性を点数として算出)だけでなく,きょうだいの同一保育所への入所希望も考慮します.“Matching with Couples”という問題であり,学術的にも難しいことが知られています.図1は申請者が不満に思うパターンを示しています.この種の不満が生じない優れた選考結果を「安定マッチング」といいますが,その存在すら保証されておらず,納得がいく調整は容易ではありません.
不満 (a) 第1希望に自分より点数が低い子がいる
不満 (b) 第3希望に兄妹そろって入園できたはず
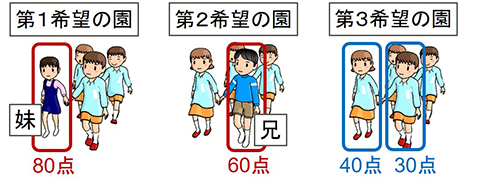
図1:申請者が不満に思うパターン
実際,各自治体では試行錯誤に多くの人手と時間を要しており,自治体によってはきょうだいが別々の保育所となるケースが増えるなどの問題が生じていました.そこで,IMIの富士通ソーシャル数理共同研究部門(2014 年 9 ⽉〜2017 年 8 ⽉)では,富士通研究所とともにこの課題に取り組み,公平な利用調整を実現する新しい方法(展開形ゲームの理論を用いる)を提案しました.提案した方法は富士通株式会社で製品化されており,実際に多くの自治体で利用されています(2020 年 6 ⽉時点で 35 の自治体が導入済み).
「物流クライシス」が叫ばれる昨今,物流業界は人手不足が深刻化しており,より少ないトラックでより多くの荷物を運ぶことができる共同輸送の必要性が更に高まっています.そこで,多数の輸送ルートが登録されたデータベースの中から協力効果が高い共同輸送の組合せを瞬時に列挙して提案する共同輸送マッチング技術を開発しました.例えば,東京→金沢の輸送レーンをもつ企業からのマッチング依頼に対して,他の2企業と協力した三角輸送(東京→金沢,金沢→大阪,大阪→東京など)などを提案します(図2).その際,実車率(走行距離に占める貨物積載区間の割合)が高くなる組合せを瞬時に列挙します.単純な総当りでは多数の依頼を処理するサービスは困難です.距離の公理などを用いて実車率の上界を上手く計算することにより,正確さを損なうことなく探索範囲を絞り込んでいます.本技術は日本パレットレンタル株式会社が提供する共同輸送マッチングサービスTranOpt(トランオプト)にコアエンジンとして搭載されており,既に約 180 社の企業が利用しています(2023 年 10 ⽉時点).
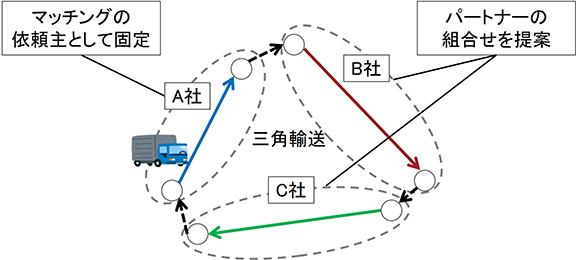
図2 三角輸送のマッチング依頼に対する処理
数値シミュレーションによる現象の理解

田上 大助
学位:博士(数理学)(九州大学)
専門分野:数値解析,計算力学
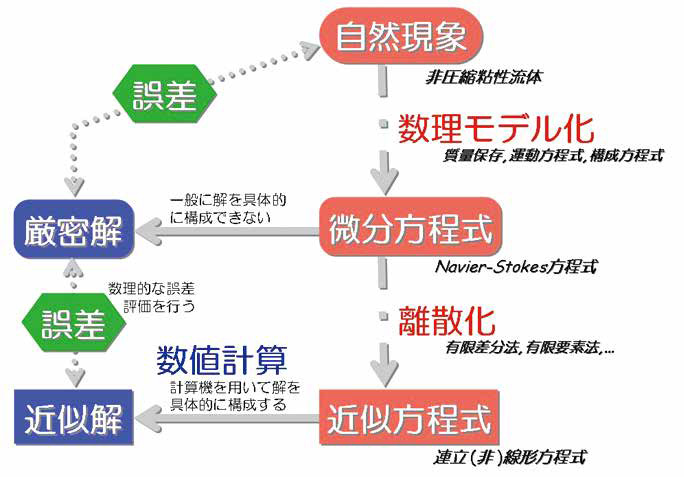
水の流れや熱の伝達など,自然界や産業界で見られる様々な現象を,計算機を用いた数値シミュレーションによって理解することに興味を持っている.数値シミュレーションでは,まず現象を物理法則に基づいて微分方程式で記述する“数理モデル化”を行い,次に微分方程式を計算機で扱うことのできる近似方程式に置き換える“離散化”を行い,最後に近似方程式の解法を計算機に実装し目的とする現象を再現する“数値計算”を行う(図1参照).我々は,提案する“離散化”手法が本来の現象に対する“精度の良い”離散化になっているか,実用に耐えうる“効率の良い”離散化になっているか,を数理的に検討する研究に取り組んでいる.また様々な問題に対して,提案する“離散化”手法に基づいた“数値実験”を実際に行い,自然現象の理解や工業製品の設計へ応用することにも取り組んでいる.
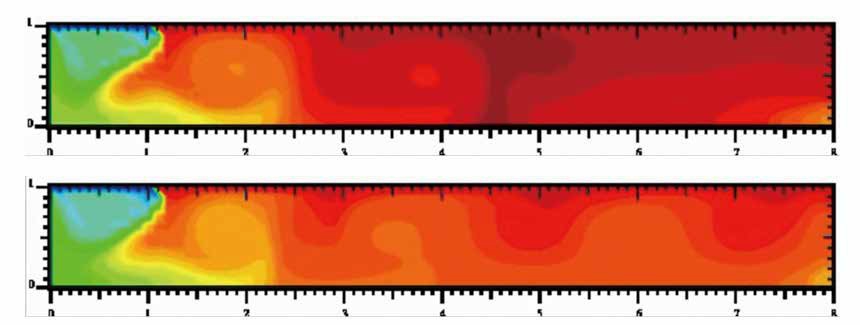
我々が取り組んでいる研究の一つに,ガラス溶融炉内部におけるガラス原料の流動や熱伝達の数値シミュレーションがある(図2参照).ガラス溶融炉内部にある高温(約1,500℃)のガラス原料は非圧縮粘性流体と見なせることから,溶融炉内部における現象は温度依存係数を持つ熱対流方程式によって数理モデル化できる.我々は時間方向に後退Euler法を,空間方向に混合型適合有限要素法を用いて得られる近似方程式の解に対する最適な誤差評価を導いた.またこの成果を発展させ,ガラス溶融炉の最適設計を行う際の指標の1つである炉全体の熱収支計算に対して整合流束法に基づく離散化手法を提案し,熱収支計算に対する最適な誤差評価を導いた.我々の誤差評価は,境界積分で定義される物理量を直接計算するよりも整合流束法を用いて領域積分に置き換えて計算した方が高精度である,という事実の数理的正当化に対応している.このように数理的正当化した離散化手法に基づく数値シミュレーションを用いて,製品品質の維持とエネルギー消費の抑制を両立したガラス溶融炉の最適設計について検討を試みている.
その他に我々が取り組んでいる研究の一つとして,変圧器内部の渦電流に代表される磁場の数値シミュレーションがある(図3参照).複雑な形状を持った領域や変化の著しい現象の数値シミュレーションを精度良く行うためには,自由度数が107(あるいはそれ以上)の近似方程式を効率良く扱うことがしばしば要求される.我々は静磁場問題に対して,既知量である電流密度の補正を考慮した混合型定式化による数理モデルを導入した.この数理モデルに対して反復型領域分割法に基づく近似方程式を提案し,さらに混合型定式化の際に現れるLagrange乗数の性質を利用した簡略化を行った.提案した手法は,必要となる行列ベクトル積演算を部分領域ごとに独立な静磁場問題を解くことに帰着できるため,計算効率向上のために用いられる並列計算に適しているという利点がある.以上のことから,提案した手法に現れるある反復計算の収束特性が改善され,計算効率が向上した.これにより,従来は解くことのできなかった大自由度モデルの解析に成功した.このように効率化した離散化手法に基づく数値シミュレーションを用いて,磁場の振る舞いをより精度良く把握することを通して,変圧器の最適設計についての検討を試みている.
さらに我々は,粘弾性流れ問題,移動境界流れ問題,光波の干渉・散乱問題などの数値シミュレーションにも関心を広げて研究を続けている.これにより,数理的正当化がなされた数値シミュレーションがより多くの現象に対して可能になると期待できる.

数論的不変式論とそれにまつわる幾何

石塚 裕大
学位:博士(理学)(京都大学)
専門分野:数論,数論的不変式論,ディオファンタス幾何学
私は主に数論的不変式論と呼ばれる分野を中心として研究活動をしています。大枠としては代数学の中の数論に属する分野です。その動機と手法から紹介します(図1)。
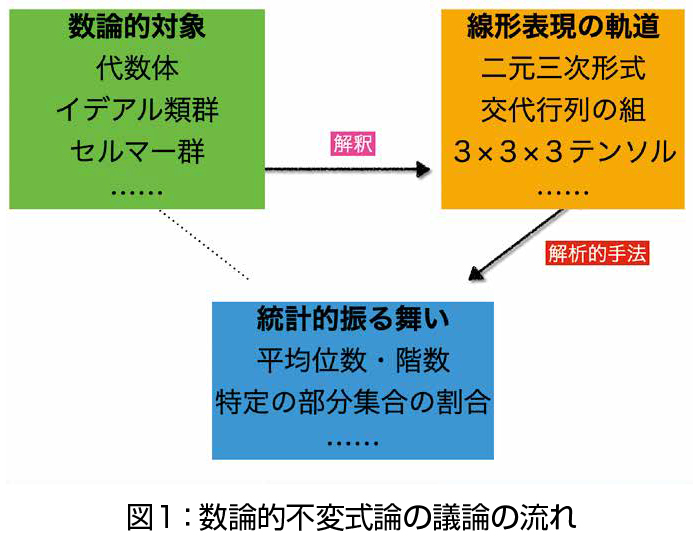
まず興味の対象は、代数体やそのイデアル類群、(有理数体上の)楕円曲線のモーデル・ヴェイユ群など、数論において重要だが扱いの難しい対象です。代数体や楕円曲線は無限に存在し、それぞれ例を作れと言われると比較的簡単に構成できます。しかし個々の例に対してイデアル類群やモーデル・ヴェイユ群を計算することは、しばしばかなり難しくなります。そしてパラメータを少し変更するとそれぞれの量は大きく変わります。
そこで、個々の例ではなく、代数体や楕円曲線全体を考えたときにイデアル類群などがどう振る舞うか、という問題を考えます。たとえばイデアル類群の『平均』位数や、モーデル・ヴェイユ群の階数が大きい楕円曲線の『割合』などを問題にします。こうした問題意識を持つ研究は総じて数論統計と呼ばれ、数論幾何、表現論、ランダム行列の理論などと結びつきながら発展しています。数論的不変式論の主な結果である M. Bhargava と A. Shankar の結果も、モーデル・ヴェイユ群の(高さに関する)平均階数の上界を与えるものです。
次にその手法です。まず数論的対象を、より取り扱いやすい代数群の線形表現の軌道として解釈します。この解釈を踏まえると、数論的対象の数え上げの問題が、ある基本領域中の格子点の数え上げに帰着される場合があります。そうした場合には、解析数論の技術と結びつけることで、もとの数論的対象についても平均・割合などが議論できるのです。私もこの流れを踏まえて、有理数体上の平面三次曲線のなかで、線形行列式表示と呼ばれる表示を持つものの割合を研究しました(例:図2)。

関連した別の研究として、ある数論的な性質を満たす曲線などの具体例を構成したり、あるいは具体的に与えられた曲線の性質を計算する研究も行っています。
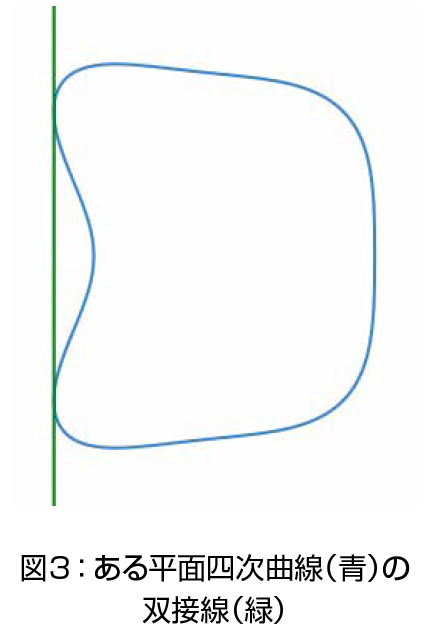
その一例が、平面四次曲線の双接線についての研究です。平面四次曲線の双接線は、その曲線と二点で接する直線、あるいは一点で四重に接する直線を指します(図3)。平面四次曲線が有理数係数で定義されていても、双接線が有理数係数で定義できるとは限りません:たとえば虚数が係数に必要かもしれません。伊藤哲史氏、大下達也氏、谷口隆氏、内田幸寛氏との共同研究では、より強く双接線が局所大域性を満たさない有理数体上の平面四次曲線を構成しました。実数やp進数の範囲では双接線が見つかるものの、有数係数では見つからない曲線です。
こうした方向性では、平面三次曲線の変曲点についても同様の考察を行っているほか、フェルマーの四次曲線についてその法を四としたガロア表現の決定も行っていま す。手法としては近年の結果を利用した数論幾何的な考察とともに、代数的な計算に数式処理ソフトを活用することで結果を得ています。
これらに通底するのは、代数幾何や不変式論の古典的な問題意識が、数論的な設定で新しい意味を帯びる点です。たとえば数論的不変式論で用いられた数論的対象と表現の軌道の対応の一部は、複素数体だと非常に単純な対応になってしまい、構造が却って見にくくなります。私はそういった数論的な設定で現れる構造について、数式処理の助けを借りながら研究を続けています。
Modeling of Solid-to-Solid Phase-Transformations in Shape-Memory Alloys Homogenization and Gamma-Convergence Problems for Nematic Elastomers
Pierluigi CESANA
学位:PhD (Applied Mathematics) (SISSA International School for Advanced Studies, Italy)
専門分野:Partial Differential Equations, Variational Problems
The main focus of my research work is on rigorous mathematical modeling and analysis of multiscale and multiphysics systems in materials science. My investigations explore ways information and disorder emerge and evolve generating complexity and patterns in smart materials such as martensite, nematic elastomers and liquid crystals. Understanding the microscale features and mechanisms of multifunctional materials and predicting their interactions on the overall macroscopic properties is of strategic importance in the design of materials for engineering applications. Two specific lines from my past and current research are summarized below.
1) Solid-to-solid phase-transformations in shape-memory alloys
Austenite-to-Martensite phase transformation is observed in various metals, ceramics and biological systems. It is the activation mechanism of the Shape-Memory effect. Despite the vast potential to the shapememory effect, practical implementations have been slow, and to-date, mostly limited to NiTi. It is strategically important to improve and stabilize the shape-memory effect in known materials and develop new modeling strategies. A problem I have considered is the analysis and modeling of disclinations (topological defects at the lattice level characterized by rotational mismatch). Disclinations as in Fig. 1-a are characterized by a self-similar triple-star pattern resulting in intense rotational stretches. Mathematically, I have shown that such configurations arise as a solution of differential inclusion problems with special rotational symmetry and rigidity. By identifying the basic algebraic structure underlying the differential inclusion I have computed exact solutions both in linearized and finite elasticity models shedding light on the mechanism that drives formation of triple-stars. Moreover, I have investigated onset of criticality and self-organization in the evolution of martensite via sequential avalanching. Here the modeling strategy describes the nucleation of martensitic variants as a branching random walk process (see Fig. 1-b). The question that I addressed is the behavior of certain features of the self-similar structure thus formed and the computation of power laws for the length interfaces in a martensitic transformation. This project involved collaboration with the groups of J. Ball and B. Hambly (Oxford, stochastic modeling of martensite); E. Vives and A. Planes (Barcelona) and T. Inamura (TiTech) on experiments on avalanches and disclinations in martensite. Work is in progress on the investigation of the activation mechanisms that drive avalanches in metals with the ultimate goal of mechanically characterizing the dynamics of solid-to-solid phasetransformations.
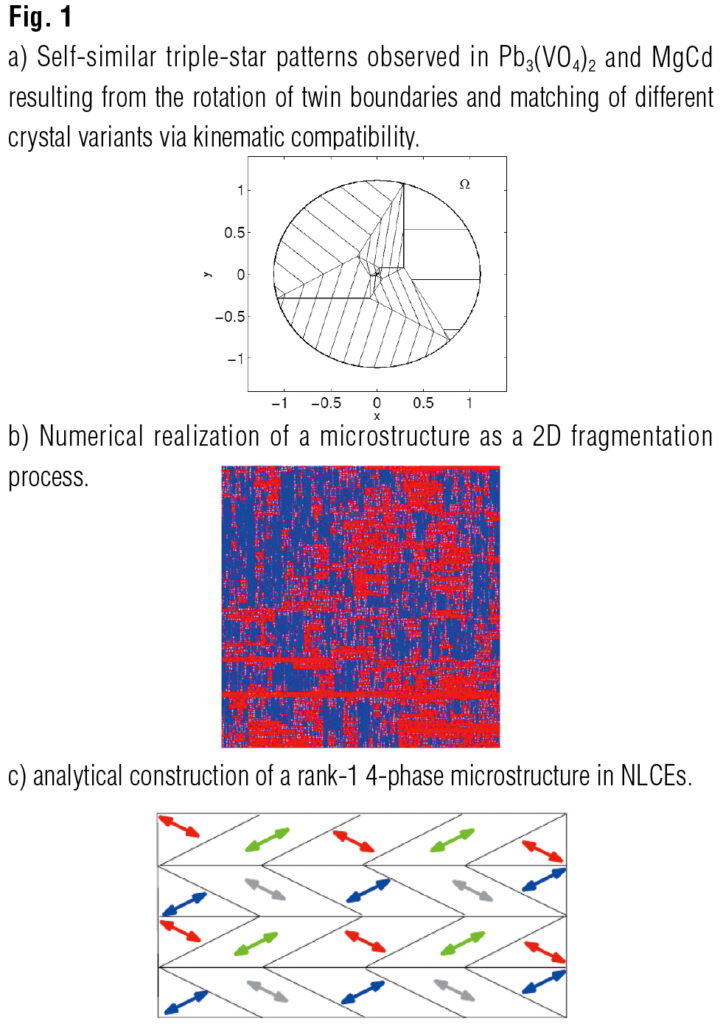
2) Homogenization and Gamma-Convergence problems for nematic elastomers
Nematic Liquid Crystal Elastomers (NLCEs) are a class of soft ShapeMemory Alloys that combine the entropic elasticity of a network of crosslinked polymeric chains with the peculiar optical properties of nematic liquid crystals. A thorough understanding of the manipulation of optical birefringence in thin-films of NLCEs by mechanical, electric and thermal means is a tremendous mathematical task which has strategical potential applications in materials design and fundamental sciences. Focusing on the strain-order coupling in NLCEs, I have investigated mechanisms that rule the low energy states in mechanically and geometrically constrained systems such as artificial muscles, sensors and actuators. The mathematical language required to tackle NLCEs problems is that of calculus of variations, Gamma-convergence and relaxation. These are sophisticated techniques at the intersection of the analysis of PDEs, functional analysis and measure theory based on energy minimization approach and which are particularly suitable for the study of singularly perturbed variational problems. Collaborations are in progress with the experimental Lab of K. Urayama (KyotoTech).
Algebraic specification

Daniel GAINA
学位:PhD (Japan Advanced Institute of Science and Technology)
専門分野:Universal Logic, Formal Methods, Category Theory
Universal logic is a general study of logical structures with no commitment to any particular logical system in the same way that universal algebra is a general study of algebraic structures. The term “universal” refers to the collection of global concepts that allow one to unify the treatment of the logical systems and avoid repetition of similar results. One major approach to universal logic, in terms of both number of research contributions and significance of the results, is institution theory. This relies upon a category-based definition of the informal notion of logical system, called institution, which includes both syntax and semantics as well as the satisfaction relation between them. As opposed to the bottom-up methodology of conventional logic tradition, the institution theory approach is top-down: the concepts describe the features that a logic may have and they are defined at the most appropriate level of abstraction; the hypothesis are kept as general as possible and they are introduced only on by-need basis. This has the advantage of proving uniformly results for a multitude of logical systems. It leads to a deeper understanding of the logic ideas since the irrelevant details of particular logics are removed and the results are structurally obtained by clean causality. My research interests cover, roughly, institution theory and its applications to computing science.
(1) Foundation of system specification and verification
There are many contributions of institution theory to computing science, the most visible one is providing mathematical foundations for the formal methods techniques, i.e. specification, development and verification of systems. In algebraic specification, one of the most important classes of formal methods, it is a standard and mandatory practice to have an institution to underlie each language basic feature and construct; institution theory sets a standard style for developing an algebraic specification language that initially requires to define a logical system formalized as an institution and then develop all the language constructs as mathematical entities in the framework provided by the underlying institution.

(2) Reconfigurable software systems
The main direction of my research consists of developing logical structures supporting the efficient development of correct reconfigurable software systems, i.e. systems with reconfigurable mechanisms managing the dynamic evolution of their configurations in response to external stimuli or internal performance measures. A typical example of reconfigurable system is given by the cloud-based applications that flexibly react to client demands by allocating, for example, new server units to meet higher rates of service requests. The model implemented over the cloud is pay-per-usage, which means that the users will pay only for using the services. Therefore, the cloud service providers have to maintain a certain level of quality of service to keep up the reputation. Generally speaking, reconfigurable systems are safety- and securitycritical systems with strong qualitative requirements, and consequently, formal verification is needed.

(3) System development
I am currently maintaining the Constructor-based Theorem Prover (CITP), a proof management tool built on top of an algebraic specification language for verifying safety properties of transition systems. The methodology supported by the tool is not intended for formalizing mathematics, but for the application to the development of software systems. In order to achieve the targeted goal, the following important research directions are pursued:
(a) proposing more expressive logical systems to allow engineers to specify easily and accurately the software systems,
(b) develop decision procedures that can reason efficiently about these more sophisticated logics, and
(c) improvements of the proof assistant interface to help the user understand the current state of the proof and interact with the tool in a more natural way.
The interest is in the design of software systems as one can see in the table below.
The system will be specified at the most appropriate level of abstraction depending on the requirements for its behavior. The result of the verification performed with the tool will determine if improvements of the design are required or not.