Please use your browser's print function to print or convert to PDF.
Only A4 paper size is supported.
Discrete Optimization and its Applications

KAMIYAMA, Naoyuki
Degree: Doctor of Engineering (Kyoto University)
Research interests: Discrete Optimization, Graph Theory, Computational Complexity
I carry out research of the theoretical aspects of discrete optimization. My main fields of interest include graph theory and computational complexity, which are deeply related to discrete optimization. These fields lie at the intersection of mathematics and computer science, and there is great interaction between them. The main problem in which I am presently engaged is to obtain a unified understanding of these fields by using submodularity, which is a discrete analogue of convexity and polyhedral approaches based on duality. In the following, I will briefly explain these fields and the problems I am investigating in my research.
The numbers represent preference lists. (right) An example of an assignment.
Let me first explain discrete optimization. Optimization is the problem of finding a solution that maximizes or minimizes an objective function among all feasible solutions. Discrete optimization deals with optimization problems possessing discrete structures. In this field, we attempt to determine which properties enable us to find an optimal solution without checking all feasible solutions, and we derive methods for finding optimal solutions (called algorithms). I am presently studying stable matching problems, in which one attempts to find an optimal assignment between two groups (see Figure 1). I am also studying network flows that model flow through a network and matroids and submodular functions, which are abstract frameworks for discrete optimization.
Next, I explain graph theory. A graph consists of vertices and edges connecting vertices. Edges represent topological relationships among vertices (see Figure 2). Intuitively, a graph can be understood as a mathematical model of a road network in an urban area. In graph theory, we try to elucidate general properties of graphs. For example, we attempt to determine whether graphs are sufficiently robustness for some purpose. I am presently studying min-max theorems concerning packing arborescences (see Figure 2) and the edge-dominating set problem, which is one of the most fundamental optimization problems in graph theory.
Finally, I explain computational complexity. Roughly speaking, the goal of the above two fields is to understand what we can do. Contrastingly, the aim of computational complexity is to understand what we cannot do, i.e., the limits of our computational capability. More precisely, in this field we formally define abstract models of computation and study the limitations of these models. The P vs NP problem proposed by the Clay Mathematics Institute is a central problem in this field. At first glance, optimization and computational complexity seem to be, in some sense, opposites. However, there is a deep connection between these fields. Recently, techniques in optimization have been used for analysis in computational complexity. I am interested in the application of optimization techniques (e.g., the polyhedral approach) to computational complexity. I am also interested in applications of optimization techniques to real-world problems arising in urban planning, the design of transportation systems and social networks.
Modeling, Analysis, Optimization, and Control of Complex and Networked Systems

Hoa Dinh NGUYEN
Degree: PhD (Information Science and Technology) (The University of Tokyo)
Research interests: Modeling, optimization and control toward low-carbon and autonomous energy, transportation and other interconnected, complex systems. Particular focuses are on renewables and distributed energy resources, smart grid, intelligent transportation, multi-agent systems, graph theory, artificial intelligence, and decentralized optimization.
My research theme is Modeling, Analysis, Optimization, and Control of Complex and Networked Systems. The research goal is theoretical approaches for the modelling, exploration, analysis, and optimal, robust and resilient decision-making for complex and networked systems. To achieve that, a variety of mathematical framework will be employed, for example, dynamical systems and their stability theories, linear and nonlinear optimization, graph theory, control theory, differential geometry, bifurcation theory, and artificial intelligence.
Particular application areas include smart grid, smart cities, renewable and distributed energy systems, cyber-physical systems, wireless power transfer, intelligent and decarbonized transportation systems, bio systems for clean energy production and carbon capture. An illustration for smart grids, an example of such complex systems, is depicted in Fig. 1.
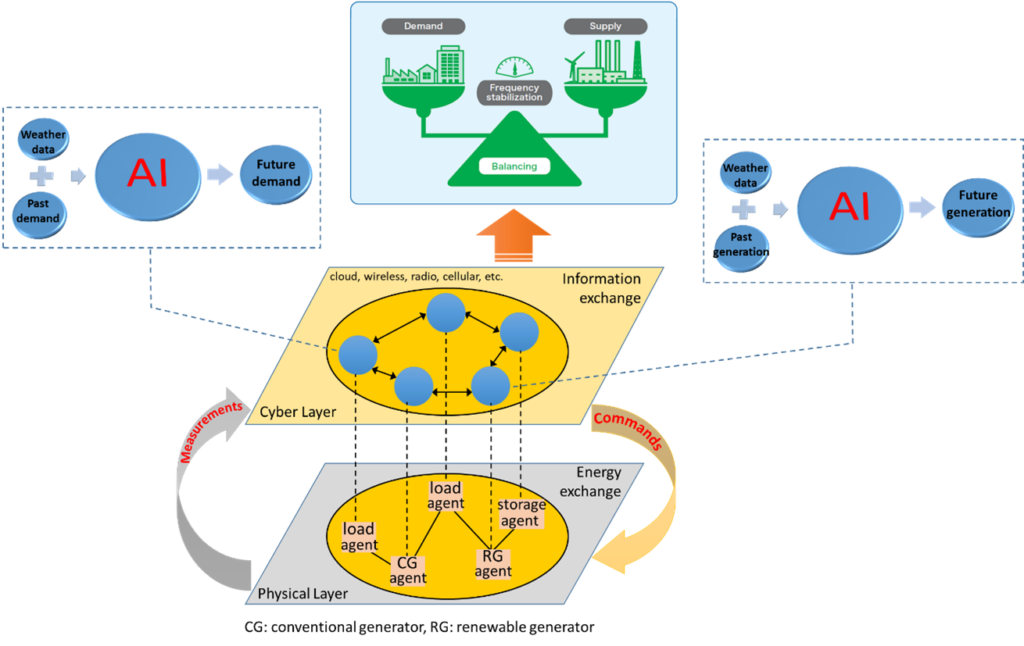
Figure 1. Illustration for modeling, decision and control in smart grids.
Mathematical analysis of the parabolic PDEs via the harmonic analysis

Taiki Takeuchi
Degree: Doctor (Science) (Waseda University)
Research interests: Parabolic PDEs, Harmonic analysis
I mainly study the parabolic partial differential equations (PDEs), where “parabolic” means one of the classifications for the PDEs and the typical example might be the heat equation.
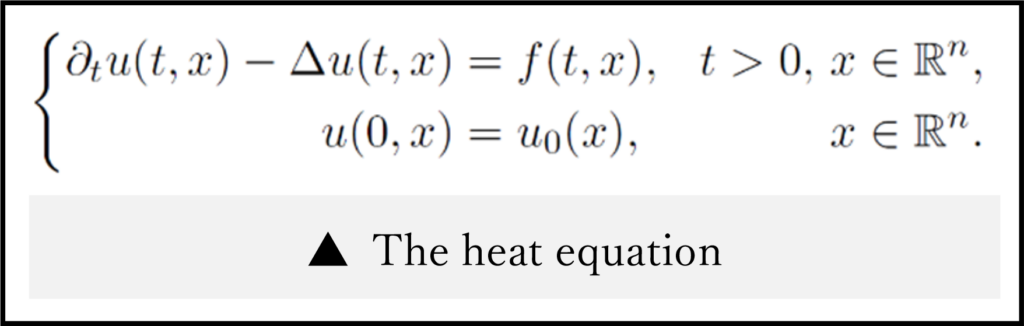
For instance, when a frying pan is heated, the transition of its temperature is dominated by the heat equation: Of course, phenomena in the real world should depend on numerous external factors. However, in ideal situations, various physical phenomena are expressed via differential equations. Indeed, the parabolic PDEs may describe physical phenomena other than the heat equation. Such examples are the Navier–Stokes system, which is the equation of motion for the incompressible viscous fluid (e.g., water), and the Keller–Segel system, which is a mathematical model describing a cell-moving phenomenon via the reaction of certain chemical stuff (chemotaxis).
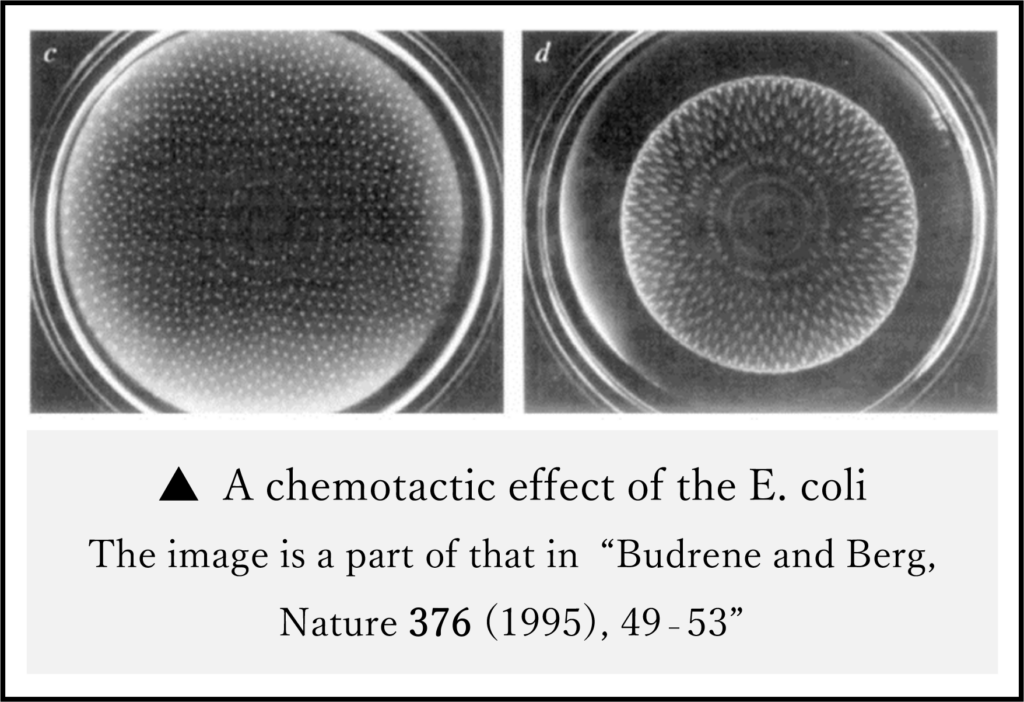
The Navier–Stokes system is the foundation of fluid dynamics and supports various applied fields in the real world. In addition, the Keller–Segel system is applied to the phenomena of cancer metastasis and Alzheimer’s disease, and hence it plays a crucial role in the development of medical technology. In this way, the mathematical analysis of the (parabolic) PDEs is closely related to various issues in the real world.
Let us consider how to analyze the parabolic PDEs: The most fundamental question from the viewpoint of the differential equation theory might be “whether solutions exist or not”. If the differential equation describes a physical phenomenon exactly, then such a phenomenon should be forecast by relying only on numerical simulations without any theoretical analysis. However, it is unclear whether such an equation expresses the corresponding phenomenon exactly; there is a possibility that the equation does not have a solution in the mathematical sense. We thus need to find exact solutions, which is one of the motivations of the mathematical analysis. In particular, as for me, I would like to extend the mathematical conditions ensuring the existence of solutions.
Here let us introduce the keyword “Harmonic analysis”: There are several ways to investigate differential equations mathematically. In particular, I rely on the method that is based on the harmonic analysis. Many people have heard of the word “Fourier transform” somewhere; harmonic analysis means the analysis using the Fourier transform.
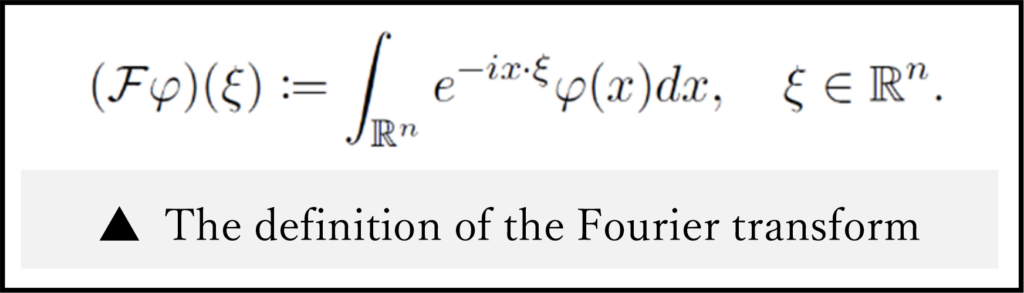
Introducing suitable function spaces would be necessary for the mathematical analysis of differential equations; the function spaces based on the harmonic analysis are a strong tool in my research method. In particular, the useful point is that the smoothness of functions is expressed by the increasing rate corresponding to the functions’ frequency, unlike differentiability.
There have been numerous works on the (parabolic) PDEs via harmonic analysis: While various results have been obtained, further developments are also expected in this direction. I hope that my work will help such developments even a little.
Discrete Differential Geometry and Integrable Systems

KAJIWARA, Kenji
Degree: PhD (Engineering) (the University of Tokyo)
Research interests: Discrete Differential Geometry, Integrable Systems, Painlevé Systems, discrete and ultradiscrete systems
My research activities are based on the study of integrable systems, which originates from the study of nonlinear waves with a particle-like characteristic called solitons. In mathematics, although fundamental equations to describe solitons are nonlinear partial differential equations, which are generally difficult to analyze, they possess a miraculous property in that they can be exactly solved. Behind such miracles lies the mathematics of infinite-dimensional space with the symmetry of infinite degrees of freedom. A family of functional equations that share this property is called integrable systems. A deep understanding of the underlying mathematics of integrable systems enables various applications. Three such examples follow.
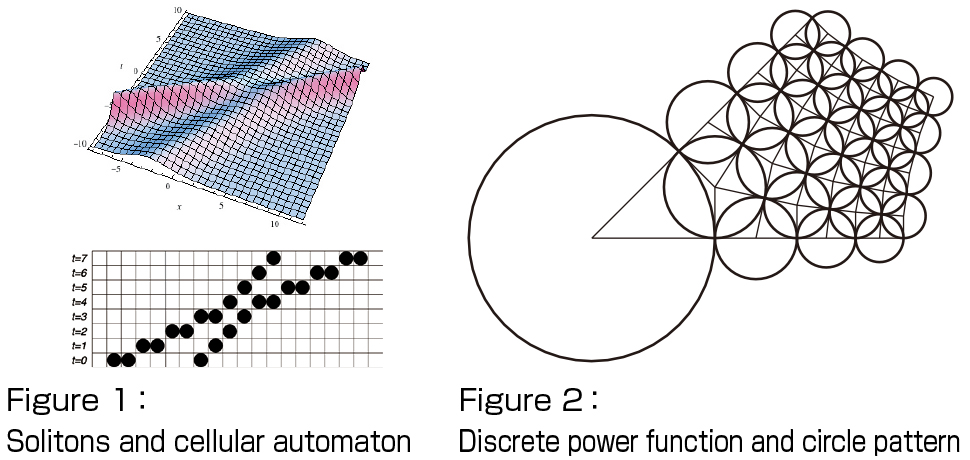
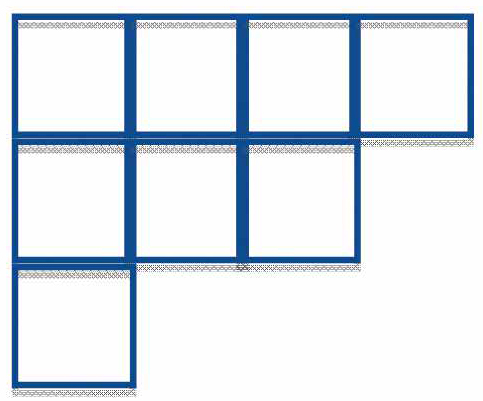
1. Discretization and ultra-discretization: A method to discretize both independent and dependent variables of the soliton equations preserving the integrability has been developed (ultra-discretization). A typical interaction of solitons is shown on the top of Fig. 1, where a large soliton with a higher velocity comes from the left and passes a smaller, slower soliton. An automaton that describes solitons is shown on the bottom of Fig. 1. There are rows of boxes and balls. At each time stop, from the left to the right, each ball is moved to the empty box closest to the right once, and the time is incremented by one when all balls have been moved. This simple model describes solitons, and a sound correspondence to a partial differential equation can be established through ultra-discretization. Discretization and ultra-discretization preserving integrability have been applied to a wide range of mathematical sciences and engineering, including numerical analysis and traffic flow analysis, and this is my theoretical backbone of the collaborated activities with other area, in particular, those related to geometry (discrete differential geometry). Recently, applications of the ultra-discretization have been extended to the non-integrable diffusionreaction systems so that many reaction-diffusion cellular automata have been constructed. In addition, the underlying geometric structure of ultradiscrete systems has recently been clarified in terms of tropical geometry.
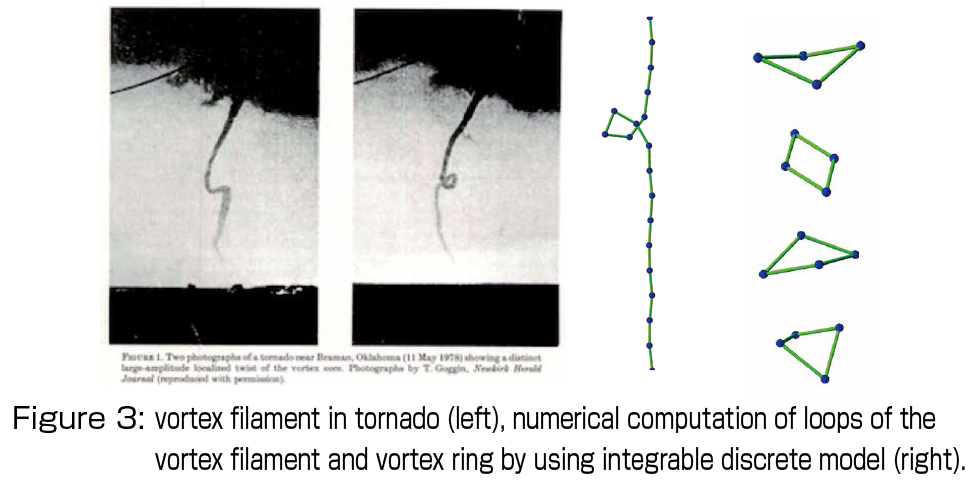
2. Discrete Painlevé equations and elliptic curves: A family of difference equations called discrete Painlevé equations is formulated as an addition theorem on moving pencils of cubic curves in the complex projective plane. Their solutions can be regarded as the generalization of the special functions of hypergeometric type, such as the Bessel functions. On the top of these equations there lies the elliptic Painlevé equation with the symmetry of E8 (1) type, and the elliptic hypergeometric function expressible by the elliptic theta functions arises as the particular solutions. This function is considered to be at the top of all the hypergeometric type special functions. As an application, discretization of certain complex regular functions can be described by the (discrete) Painlevé equations. Figure 2 illustrates the discrete power function Z1/2, where the grid is characterized by the circle patterns.
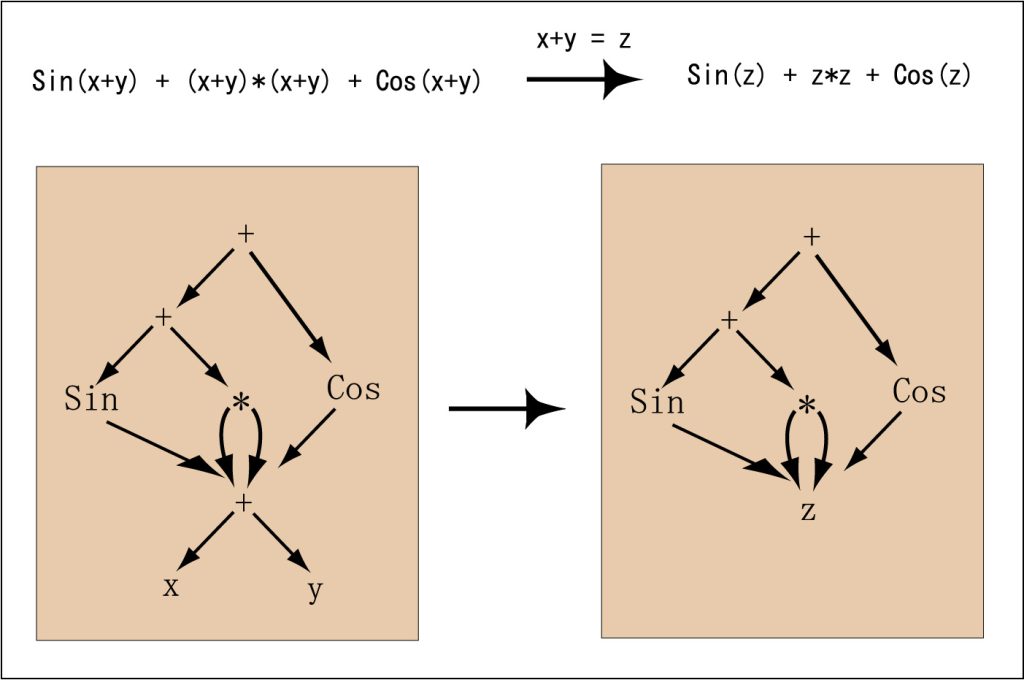
3. Discrete integrable differential geometry and geometric shape generation: Various integrable sytems arise as the fundamental equations describing the space curves and surfaces and their deformations. Further, recently, the theory of curves and surfaces consistent with the discrete integrable systems advanced, so that I am now developing the geometric shape generation, in particular, generation of “good” curves and surfaces in a certain sense, collaborating with the experts of industrial design and architecture. Figure 3 shows the typical dynamics of tornados, namely natural vortex filaments (left), and the results obtained by the integrable discrete model (right). It gives high quality results with low-cost computation since the underlying structure is preserved. Figure 5 (left) is a family of plane curves called the logaesthetic curves which was proposed in Japan as shape elements of CAD with built-in aesthetic property, and they were extracted from the shapes which we think beautiful, such as Japanese swords and butterflies (Figure 4). Recently, we have proposed a new theoretical framework from the standpoint of the integrable geometry, from which we constructed the high-speed and high-quality discretization and a space curve extension (Figure 5 right). We develop this theory to the surfaces, and implement the family of curves and surfaces with aesthetic character as the geometric shape elements, and eventually we aim at standardization of those shape elements in the area of industrial design. Those shapes would serve as important examples of mathematical models incorporating the element of human feeling of “aesthetics”: Good equations can generate good shapes.

Theoretical Computer Science and its Applications

MIZOGUCHI, Yoshihiro
Degree: PhD (Science) (Kyushu University)
Research interests: Computer Science
The graph structure has been a subject of research and application even before computers were created, as it is a basic tool to intuitively describe a complex situation. However, since the introduction of computers, the graph structure has been used not only for internal expression within a computer program (data structure), but also as a newly devised computational system to execute a computation by rewriting the graph itself. These advances have made conducting research on the property changes of a graph due to an operation on the graph (graph rewriting theory) particularly important, in addition to the conventional research on static graph structures (graph theory). Moreover, a viewpoint is needed for constructing an algorithm based on the assumption that a computer’s hardware has a certain kind of basic graph rewriting operation, rather than graph rewriting operation being implemented on an existing computer. There have been many research projects recently to devise and design computers within the framework of natural computation, such as molecular computation and quantum computation, which necessitate the fundamental theory of computation using graph rewriting theory.
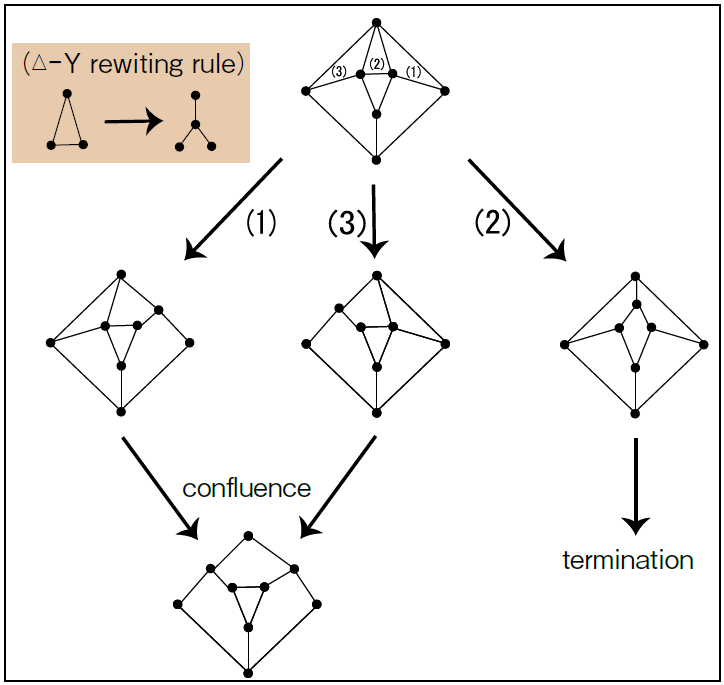
Formula translation with a computer is executed by expressing a formula using a tree structure and by altering part of the tree corresponding to a pattern to calculate or transform the formula. Graph rewriting improves the computation efficiency by expressing a formula with a graph structure that shares the same terms within the formula (Fig. 1). In this process, a pattern matching algorithm for the graph structure and a graph formalization that does not change the meaning of a formula are important.
Graph rewriting procedures can be computed simultaneously as long as the rewriting computation regions do not overlap. Computation algorithms using graph rewriting have been developed for computations such as the shortest path length in traffic networks, the reliability of networks, and impedance in an electrical circuit. Computations using a rewriting do not always produce the same computation result because computation processes branch out due to application locations and the application order of rewriting (Fig. 2). For this reason, it is important to theoretically confirm that these branches are always confluent or to construct rewriting rules to derive the same computation result.
Computation by transforming a graph, which is a connection of points on a straight line, is closely related to computation using a cellular automaton, which is applied to modeling physical phenomena (Fig. 3). A molecular computation, which uses a DNA strand as in a gene, is considered a possible device to directly achieve a computation mechanism using a cellular automaton. Theories of computability for a graph rewriting system and cellular automaton, computational universality, and computational equivalence can be used to evaluate the effectiveness of computer performance.
Formulating a simultaneous parallel computation of graph conversion and demonstrating computation convergence, algebraic methods, including discrete mathematics, relational algebra theory using binary relations, and category theory are necessary. Furthermore, evaluation of computability requires automata and language theory, computation theory, and mathematical logic theory. Theoretical computer science is not only the theory of data structures and algorithms to be used with current computers, but also the theory of logic and computation to design and devise computers for future computer architecture.
Our research group is conducting research in mathematics and theoretical computer science to revolutionize technologies utilizing computers, which are the foundation of our modern information-based society, as well as to develop novel computation mechanisms.
Adaptive Network Theory with Organism

TERO, Atsushi
Degree: PhD (Science) (Hokkaido University)
Research interests: Mathematical Modeling, Network Theory
During an organism’s long-term struggle for existence, it evolves many refined techniques for life phenomena. I transcribe such life phenomena to numerical formulas in my work. I also extract the techniques from the organisms and apply them industrially.
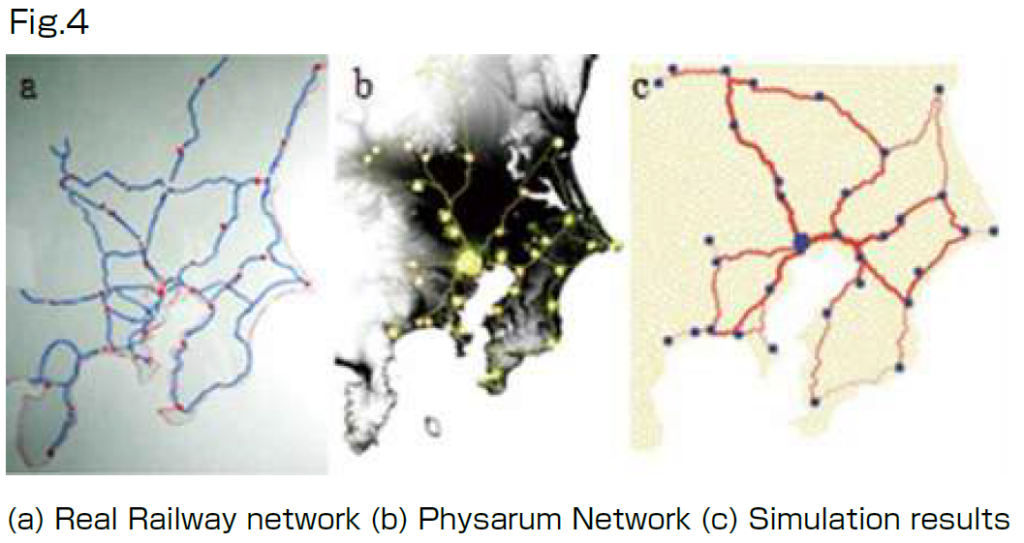
There are various types of transportation networks, such as railway networks, ant trails, blood vessel networks, and leaf veins. Commonly used paths develop in these networks, while paths that are not frequently used degenerate. These networks are called “adaptive networks”. The network topology of an adaptive network varies (such as capillaries and the aorta). The purpose of my study is to understand the formation of such an adaptive network.
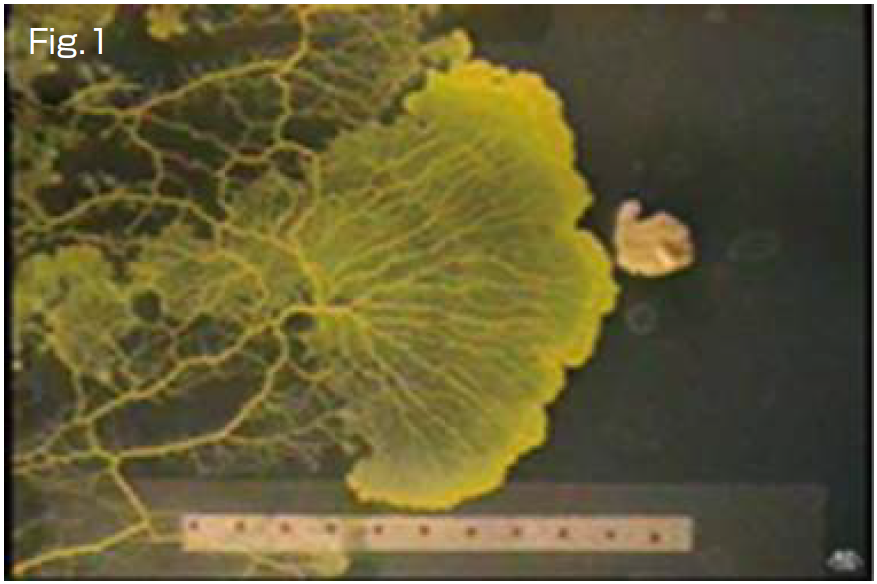
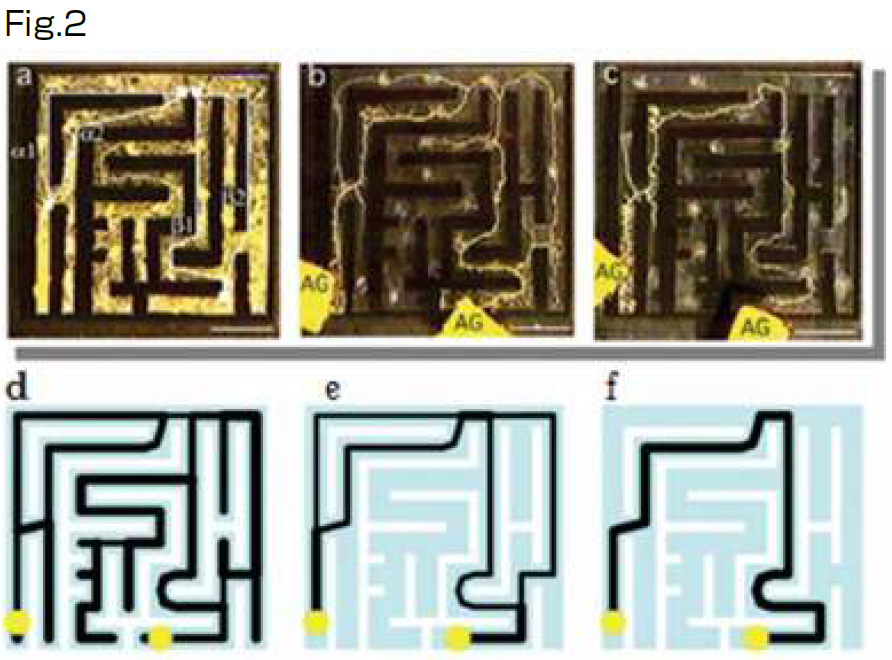
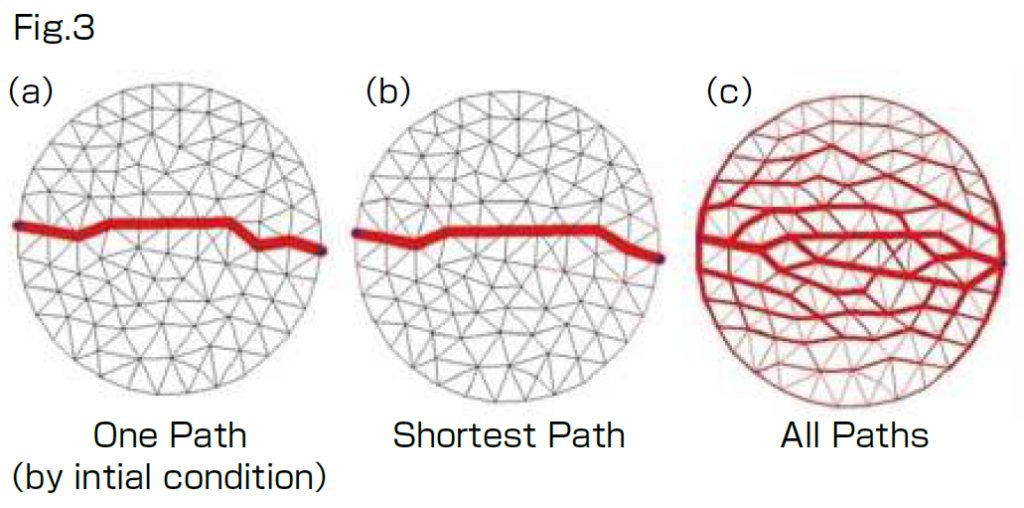
A true slime mold, Physarum polycephalum, was used for this study (Fig. 1). This slime mold is a unicellular organism, but it has the collective property of containing many nuclei. For example, if it is cut into pieces, each piece can live as an individual. However, the pieces can also fuse and become one living individual. The mold has an adaptive network to transport nutrients. It is a superior specimen for understanding adaptive networks because it can be cut and handled in this way. The transportation network of this slime mold is a product of its solving of mazes (Figs. 2a-c) and is an optimal network (Fig. 3b), according to my co-worker Prof.
Toshiyuki Nakagaki (Future University-Hakodate). However, how the slime mold solves the network problem without a brain or global information remains unanswered.
I reproduced this phenomenon by describing it with numerical equations (Figs. 2d–f). The parameter to solve the maze was found to be the boundary of the network topology. When the growth rate of a thick path is strong, it is the only path that remains (Fig. 3a) because a thick path at the initial state easily grows and further growth also becomes easy. Conversely, if the maintenance cost is high for a thick path, the path cannot maintain its thickness, and the other paths remain (Fig. 3c). The parameter for solving the maze is the boundary of these two types of network formation (Fig. 3b).
I applied this common theory of adaptive networks to a real railway network (Figs. 4a–c). I will also apply it for various adaptive networks. In addition, I study action control using a variety of rhythms and voluntary morphosis of organisms.
Development of Optimization Techniques and Software

WAKI, Hayato
Degree: Doctor of Science (Tokyo Institute of Technology)
Research interests: Optimization, Mathematical Programming
The optimization problem is that of finding the maximum or minimum of a given function over a given set. This problem is widely confronted in industry, as well as daily life. In a recent public statement, IBM asserted that BAO (business analytics and optimization) and the importance of optimization in business are rapidly becoming more and more prominent.
My main research interests are the following: (i) to solve continuous optimization problems, e.g., convex optimization problems and semi-definite programming problems (SDPs); (ii) to develop effective algorithms and software. I am particularly interested in developing methods to solve nonlinear and nonconvex optimization problems by using convex optimization and SDPs. In fact, my collaborators and I have proposed an efficient approach for determining global solutions of optimization problems that are described by polynomials. I refer to such optimization problems as polynomial optimization problems (POPs). We have demonstrated that our approach is effective for POPs that possess a sparse structure. In general, it is known that finding a global solution of a POP is NP-hard. Lasserre and Parrilo independently proposed approaches that use SDPs for the purpose of solving POPs. Although their results are very nice from the theoretical point of view, they are not effective for POPs with more than 20 decision variables. With our approach, some POPs with more than 100 variables can be solved. In this work, we developed the software SparsePOP for solving POPs. This is open-source software and is available at the following site: SparsePOP http://sourceforge.net/projects/sparsepop/
As an application of POPs, we have treated a number of sensor network localization problems, which arise in monitoring and controlling applications in which wireless sensor networks are employed, such as gathering environmental data. Although GPS technology is more suitable than wireless sensors for this purpose, it is usually very expensive for such applications, and thus it is not a feasible option. For this work, we proposed an approach based on our work related to POPs and developed the software SFSDP. This is also open-source software, and it is available at the following site: SFSDP http://www.is.titech.ac.jp/~kojima/SFSDP/SFSDP.html
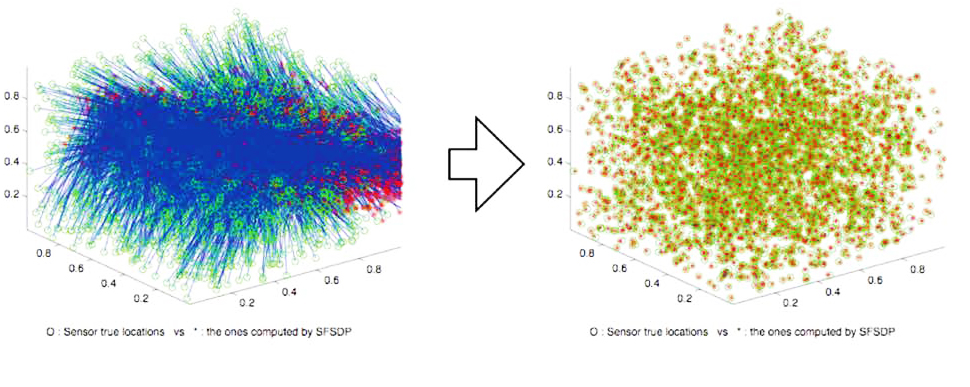
The figure demonstrates that we can accurately estimate the locations of sensors from distance data with noise using the SFSDP software. The blue lines in the figures represent the differences between the actual locations of the sensors and the locations determined using two methods. The data in the left figure were obtained using an existing method, while those in the right figure were obtained using our method with the SFSDP software. In the left figure, there are many long blue lines. It is thus seen that the existing method cannot accurately estimate the locations of the sensors. Contrastingly, the right figure contains no such long blue lines, and we thus conclude that our method employing the SFSDP software is capable of estimating the locations of the sensors with much greater accuracy.
There are two main difficulties involved in our approach to treating POPs: (1) the resulting SDPs still are too large to handle in the case of POPs that do not possess sparse structure; (2) the resulting problems have too great a degree of degeneracy to solve accurately. As a result of the second problem, it is difficult to find an accurate global solution. In addition, for some POPs, we often encounter phenomena in which the theoretical results differ greatly from the computational results due to numerical errors, e.g., rounding errors in the computation. We welcome collaboration with researchers who are interested in the challenge of overcoming such difficulties and/or researchers who have some practical experience in optimization problems.
Inverse problems for hyperbolic partial differential equations

TAKASE, Hiroshi
Degree: Ph.D. (Mathematical Sciences) (The University of Tokyo)
Research interests: Partial Differential Equations, Inverse Problems, Geometric Analysis
Hyperbolic partial differential equations have important mathematical features such as finite propagation of solutions and Huygens’ principle. In addition to its importance in the mathematical sciences, it has also played an important role in physics and engineering because of its ability to model various natural phenomena such as dynamics and waves. In particular, the inverse problem of determining the governing system of equations from information on existing solutions is extremely important in the mathematical sciences as an ill-posed problem. In addition, it has attracted strong attention as a tool for understanding the background of physical phenomena in detail.
Typical research problems in inverse problems for partial differential equations are the inverse source problem, which identifies an unknown wave source, and the inverse coefficient problem, which identifies an unknown physical property described by the equation. The objective is to determine whether an observer who observes waves in part of the domain of interest can identify these unknowns in the vicinity of the domain of interest or in the entire domain of interest (Fig.1).

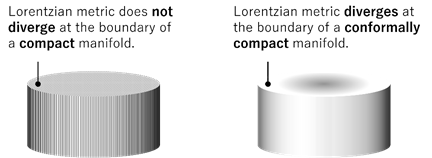
Among the various types of partial differential equations, hyperbolic partial differential equations, in particular, can often be described geometrically independent of local coordinates. Thus, for example, it is very compatible with analysis on pseudo-Riemannian manifolds that introduce indefinite metrics. In recent years, geometric analysis on compact Lorentzian manifolds has been used to study aspects of inverse problems from a geometric viewpoint. Furthermore, as an interest from physics, analysis of inverse problems on conformally compact manifolds where the metric diverges at the boundary of the manifold is also attracting attention (Fig.2). The principal part of the equations on a conformally compact manifold is degenerate, which increases the difficulty, and a new theory of inverse problems for degenerate equations needs to be developed.
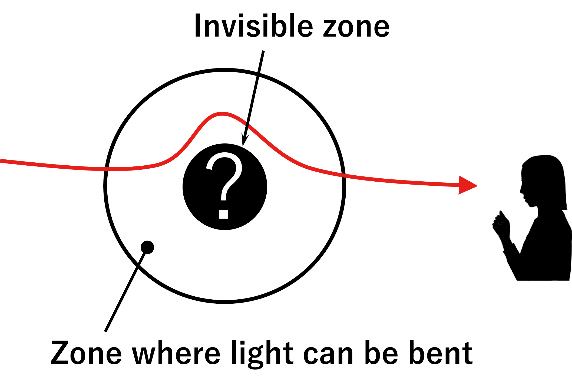
The inverse problem of identifying the unknown quantity that is the cause of the result is, of course, not always resolved in the affirmative. A negative example is light cloaking technology, such as the invisibility cloak in the Harry Potter movie. This is a technique to make an object invisible by bending the progress of light by changing the medium in a bounded domain around the object, creating an invisible zone where light from the outside does not propagate (Fig.3). In the theory of partial differential equations, changes in the medium are often formulated as potentials, which are lower-order terms. The situation in which light cannot propagate from the outside in the invisible zone due to its potential can also be understood in terms of the Cauchy problem of the wave equation with a potential term. This renewed consideration of negative situations may help in discovering mathematically interesting structures.
Algebraic Analysis: A Crossroad of Mathematics

OCHIAI, Hiroyuki
Degree: PhD (Mathematical Science) (the University of Tokyo)
Research interests: Algebraic Analysis
I’m working on mathematics, in particular, algebraic analysis. We know that most of sciences are talked in mathematical languages, experiences are often stated and examined as a formula, and complicated systems are understood as an abstract model. Algebraic analysis gives an abstract/categorical understanding of a non-commutative object/phenomenon arising in a various field. What is “non-commutativity” ? A daily example of noncommutative actions is to wear socks and to wear shoes, as the order of the actions does affect the results. At the contrary, to wear socks and to wear pants are commutative. Non-commutativity is also a source of a fun of games. For example, if the operations of Rubik’s Cube would be commutative, then it
might not be so fun and so deep. An example of noncommutativity from physics will be the Heisenberg canonical commutation relation (CCR), which is one of the characteristics of quantum mechanics. CCR is also understood in mathematics, located at the intersection of several branches of mathematics such as differential operators in analysis and Lie algebras in geometry. Representation theory serves a systematic treatment of non-commutativity, or symmetry in general, by using groups and algebras. Symmetry is technically a key to solve a complicated system, and is philosophically related with a beauty in nature.
In 1980’s, Kazhdan-Lusztig conjecture was solved by using the algebraic analysis, to be more specific, the localization of a Lie algebra by differential operators on the flag manifold. In a word, a rather complicated part of representation theory of non-compact semisimple Lie groups, an example of which is Lorentz group, turns out to have a relation with the geometry of orbits on the flag manifold. I am interested in and working on both non-commutative objects called modules and geometric objects such as orbits on homogeneous spaces and their cotangent bundles. On one hand, the category of D-modules and the operations on this category has close relation with a part of theory of special functions such as a hypergeometric function and its generalization; this is my favorite. On the other hand, the orbit decomposition on homogeneous spaces, as Bruhat decomposition is a classical example, is a source of combinatorics, which is a hard and non-trivial finite mathematics, and gives a basic example of geometry and topology, such as resolution of singularities. These two are at the same point in my mind. I am also interested in special functions arising in number theory and probability theory. I like to find the structure of unorganized data, or objects, and like to introduce a bridge between the branches of mathematics and a new viewpoint. This will help to contribute to the work at the institute of math-for- industry.

Topology and its Practical Applications

SAEKI, Osamu
Degree: PhD (Science) (the University of Tokyo)
Research interests: Topology, Singularity Theory, Differential Topology, DNA Knots
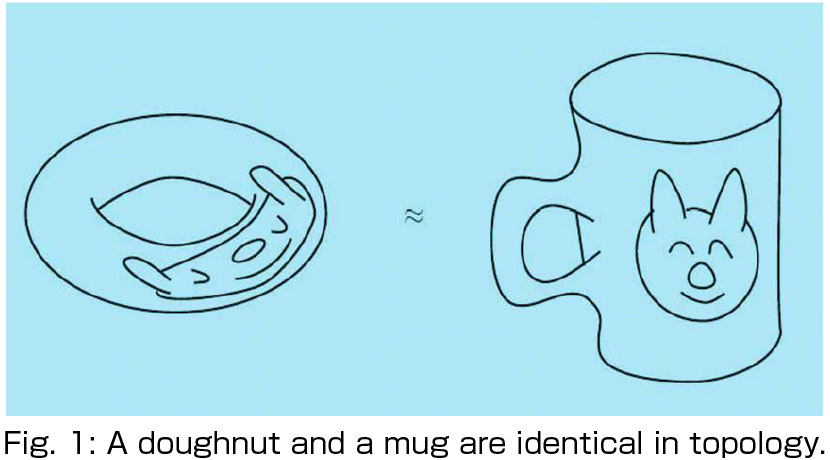
Topology is the study of extremely soft geometry, where an object is regarded as being composed of some soft material, like rubber, and a continuously deformed object is considered to be identical to the original object. In other words, topology is a field of pure mathematics in which we are interested in the properties of geometric objects that do not change as those objects are continuously deformed. For instance, a doughnut and a mug are regarded as identical in topology (see Fig. 1). This is because each of them has exactly one hole, which is a typical example of a quantity that does not change under continuous deformation.
Given its nature, topology is a powerful tool for analyzing flexible objects. One extreme such example is provided by a string, in which we can create knots and links through various manipulations. These are important actions in daily life and have been part of human existence since a primitive age. In fact, it is known that wild gorillas can tie knots. Moreover, it has recently been found that such knots are deeply connected to research into deoxyribonucleic acid (DNA).
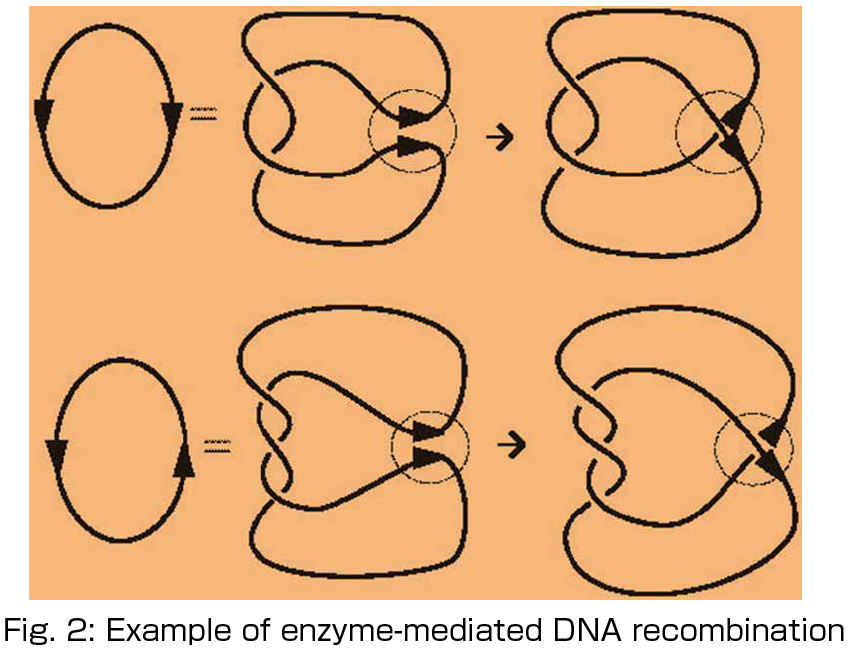
DNA, taking the form of two twisted thread-like strands, carries hereditary information and exists in the cells of living organisms. This molecule often assumes a ring-like form. Biological observations have shown that strands of ring-shaped DNA are often knotted and linked with each other. Although certain enzymes are responsible for these DNA knots and links (see Fig. 2), due to limitations in experimental techniques the details of the mechanisms involved in such processes have not yet been elucidated. In the late 1980s, the mathematicians C. Ernst and D. W. Sumners used the most recent knot theory in topology at the time to describe some of the mechanisms employed by enzymes. Although it is often said that knot theory has its origin in the electromagnetism of Gauss and the vortex atom hypothesis of Lord Kelvin from the 19th century, chemists and physicists seem to have forgotten about knots, and only mathematicians have maintained this topic as a field of research. Our group is making extensive use of knot theory, which is one of the most actively researched fields in modern mathematics, to analyze DNA recombination mediated by an enzyme called topoisomerase from a mathematical point of view (see Fig. 2). Our main goal is to apply these analyses to industrial technologies.
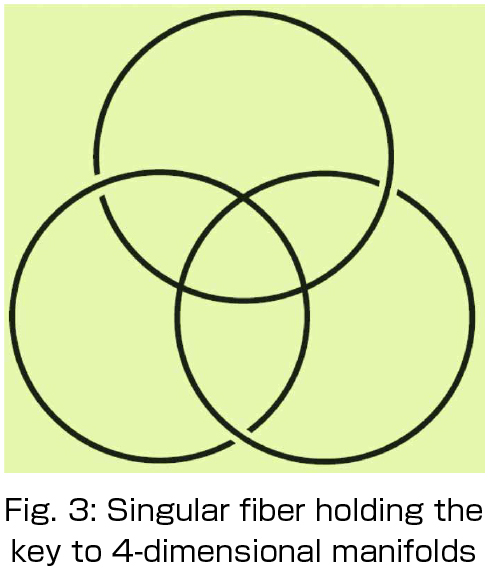
In addition to knot theory, we are actively investigating singularities of differentiable mappings, using techniques of differential topology. In particular, we have made a number of discoveries for specific cases in which singular points of mappings between smooth objects deeply reflect the topological properties of those objects. I am considered a worldwide authority on the theory of inverse images of points, called singular fibers (see Fig. 3), and I recently published the first book that formulates this theory. More recently, I have been attempting to apply the theory to visual data analysis for multivariate functions. Our group is also interested in analyzing large datasets by employing processes through which the data can be visualized and their characteristics can be grasped in a robust manner. Differential topology plays an essential role in the realization of this project.
We have also been working on a broad range of topics in topology, including separation properties of codimension-one mappings, topology of isolated singularities of complex hypersurfaces, 4-dimensional manifolds, embeddings in codimension one, and differential geometric invariants of space curves. These studies can be applied in various fields; e.g., they provide powerful tools for studying properties of materials at the microscopic level. In fact, our group has collaborated with industrial firms and found that certain topological invariants can be used to estimate physical properties of hard materials. We have thus found that although topology is a study of soft geometric objects, it can also be used to study hard objects!
My diverse research has greatly impacted my students. This fact is reflected by the broad range of the research topics studied by my master’s and Ph.D. students. In addition, some of my students have made important contributions to industrial technologies. I am also the coordinator of the WISE program “Graduate Program of Mathematics for Innovation”, nurturing doctoral talents in mathematics.
I hope that we can continue to strengthen the relationship between mathematics and industrial technologies through application of topology, a branch of pure mathematics.
Probability Theory and its Applications

SHIRAI, Tomoyuki
Degree: PhD (Mathematical Sciences)(the University of Tokyo)
Research interests: Probability Theory
Various random phenomena such as lotteries, roulettes, weather forecasts, and stock prices can be seen in everyday life.While such phenomena contain clear randomness, there are some problems to which probabilistic methods can be applied although they do not seem to be random at first glance. I am interested in finding the randomness behind such problems and studying them by using probabilistic techniques.
Here are three examples of such a situation.
(1) Kakutani’s problem, also referred to as the Collatz problem or the 3x+1 problem, is well known. In this problem, we consider a function f on natural numbers such that f(n)=n/2 if n is even and f(n)=3n+1 if n is odd. It is conjectured that repeated iteration of this function eventually produces 1 for every initial value n. For example, if one chooses initially 7, then the sequence becomes 7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1. As of 2009, this conjecture was verified up to 20X258, but it still remains unsolved at present. This problem itself is undoubtedly deterministic (non-random), but, randomness lies behind it.
In the 1960s, a Japanese mathematician Shizuo Kakutani was interested in this problem and circulated it to a number of people. Here I quote his words from a Lagarias’ paper. ”For about a month everybody at Yale worked on it, with no result. A similar phenomenon happened when I mentioned it at the University of Chicago. A joke was made that this problem was part of a conspiracy to slow down mathematical research in the U.S.” (2) The following sequence of letters is a cypher-text that is encoded by a classical method of a simple substitution cypher.
fyeaxjqfzjoxceddedcjbujcxbjhxgpjbegxrjukjzebbedcjopjsxgjzezbxgjudjbsxjofdljfdrjukjsfhedcj
Once we realize that this cypher-text is encoded by the method above, we can employ a Markov chain (one of the most basic stochastic processes) to decrypt it. The following is a simulation result of the decryption.

Some coded messages like the above written by a prisoner in the California prison system was brought into a drop-in consulting service in Stanford’s Statistics Department by a psychologist and it was decrypted by Stanford students by using Markov Chain Monte Carlo (MCMC) methods. This is a good example which shows how well MCMC works.
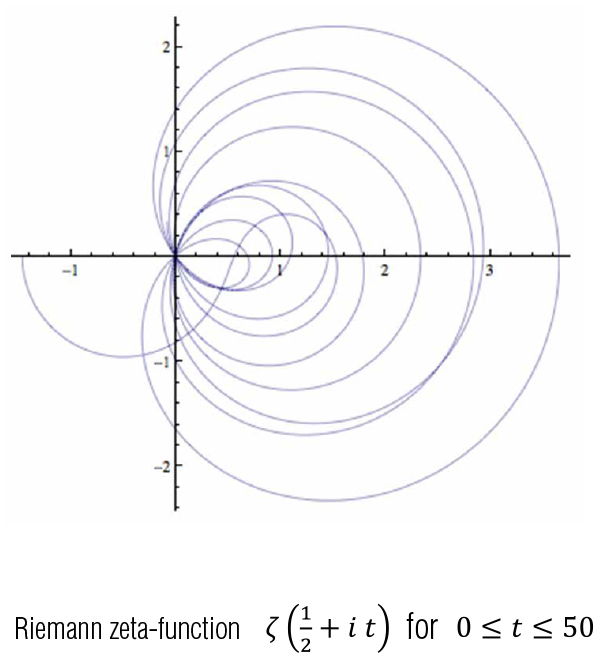
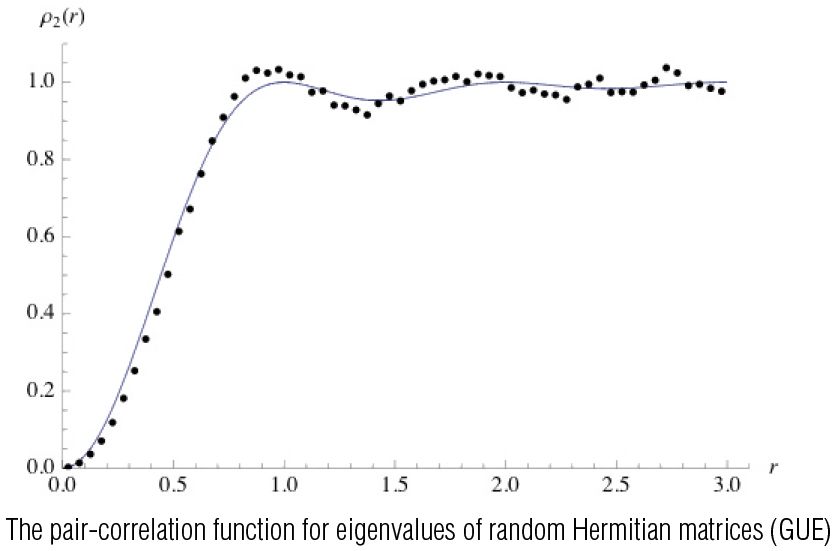
(3) The Millennium Problems are seven problems in mathematics established by the Clay Mathematics Institute in 2000. The Poincare conjecture was solved by Gregory Perelman recently, but, six problems still remain open, among which is the Riemann hypothesis. The Riemann hypothesis asserts that the non-trivial zeros of the Riemann zeta-function defined by ζ(s)=∑∞n=11ns lie on the so-called critical line Re(s)=12 The nature of this problem seems to be irrelevant to randomness, but, the zeros are known to look like the eigenvalues of certain random Hermitian matrices.
The mathematician Alfréd Rényi had said that “A mathematician is a device for turning coffee into theorems”. Freeman Dyson, a theoretical physicist, made an interesting comment on a result of Hugh Montgomery, a number theorist, during afternoon tea in the Common Room at the Institute for Advanced Study. This comment shed light on a new aspect of the Riemann zeta-function. This was the very moment that important research was turned in a new direction by a cup of coffee (tea?).
We hope that we can collaborate with one another with an open mind and in an intercultural way at IMI.
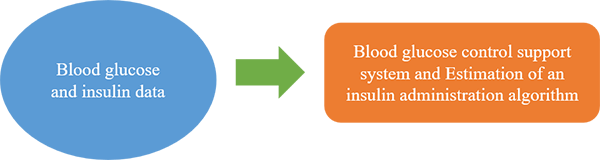
Blood glucose control from the viewpoint of mathematical sciences
KODANI, Hisatoshi
Degree: Ph.D.(mathematics)(Kyushu University)
Research interests: Topology, number theory, and arithmetic topology
Recently I have been engaged in an interdisciplinary research in cooperation with researchers of medicine and applied mathematics at other universities, investigating the control of blood glucose. More specifically, this study, using data from patients in a postoperative intensive care unit (ICU), is aimed at developing a blood glucose control algorithm that is useful in medical practice. This study is different from the fields of study presented above, but I would like to introduce it here as a study related to IMI toward the application of mathematics and mathematical sciences to industrial society.
Immediately after surgery, the blood glucose levels of ICU patients rise rapidly because of stress caused by surgical invasion, cardiotonics, and other factors. Maintaining the blood glucose level in an adequate range by insulin administration is considered important because high blood glucose concentrations can cause multiple organ failure, coma, poorer outcomes, and other complications. Nevertheless, blood glucose control by insulin is difficult because of various factors such as delayed action of insulin and variation in insulin sensitivity. Another difficulty is that seriously poor outcomes might result from hypoglycemia triggered by insulin administration. Currently, blood glucose control in ICUs is conducted by nurses under predetermined conditions. Since no standard control algorithm has been established, blood glucose control is based largely on the experience of nurses under present circumstances. Such methods of blood glucose control are a burden on them. Some standardized method must be found.

Through cooperative study, we intend to develop a standardized method to assist blood glucose control in a way that is useful in actual clinical situations, and strive to estimate an algorithm used by experienced nurses to judge insulin administration based on a combination of mathematical approaches and observations of medical practice.
Regarding mathematical approaches to such problems, mathematical models of blood glucose and insulin related to blood glucose control have been designed to date. Existing models have different capacities and objectives, with difficulties such that mathematical models which express kinetics in the body include many unmeasurable variables. Parameters that are specific to each patient must be estimated. By contrast, various new data-driven study methods have been developed in recent years in the field of data science. Our cooperative study has adopted conventional methods and novel methods in an endeavor to contribute to the development of algorithms that are better suited for the study objectives.
In cooperative studies such as those of blood glucose control, for which medical observations are important, conducting studies cooperatively with surgeons and Certified Nurse Specialists in ICUs is crucially important, not only from the viewpoint of mathematics and mathematical sciences. We will proceed steadily with cooperative studies, carefully communicating with medical specialists, and thereby improving the application of mathematics and mathematical sciences to the field of medicine and to industrial society.
Aiming at nontrivial targets with theta function

Shota SHIGETOMI
Degree: PhD(Functional Mathematics)(Kyushu University)
Research interests: Integrable Systems, Discrete Differential Geometry, Applied Physics, Theta Function
I study (1) integrable systems and related geometry and (2) applied physics, with a focus on elliptic theta functions. Elliptic theta functions are known for their rich mathematical properties and appear in a wide range of mathematical fields. In the case of my research, these properties are used to construct exact solutions to integrable systems. They are also important for discretizing equations from the information contained in the solutions and for discovering nontrivial conserved quantities. Below are some examples of applications of theta functions with specific examples.
(1) Integrable systems and related geometry:
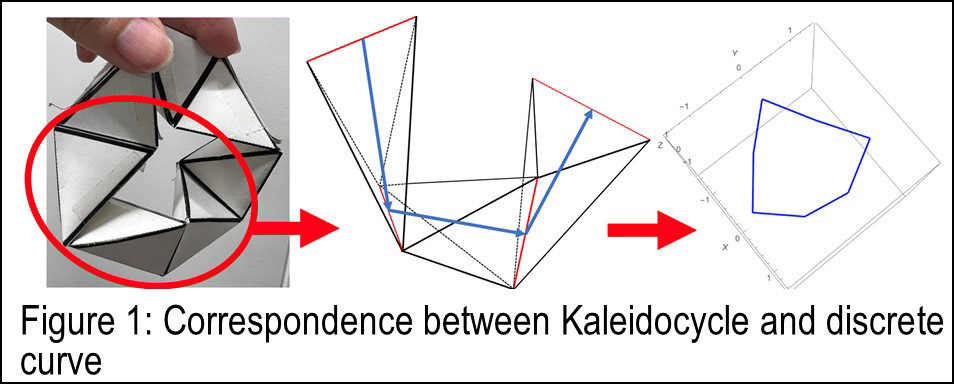
Integrable systems are a family of differential equations whose exact solutions can be constructed using well-known functions, despite their nonlinearity. There are various applications of integrable systems, but an example is the Möbius Kaleidocycle. This is a linkage mechanism consisting of six or more congruent tetrahedra connected by hinges to form a ring. This mechanism is interesting from a mathematical, physical, and engineering point of view because it has a single degree of freedom of motion, but it is usually challenging to perform a rigorous analysis of a linkage mechanism. However, if this mechanism is viewed as a discrete curve with constant torsion (Fig. 1), the deformation can be described by an integrable system, and not only the torsion and curvature of the curve, but also the position vector can be constructed explicitly using theta functions. This result has led to the discovery of previously unknown conserved quantities, etc., and is expected to play an important role in the future analysis of Möbius Kaleidocycle.
(2) Applied physics:
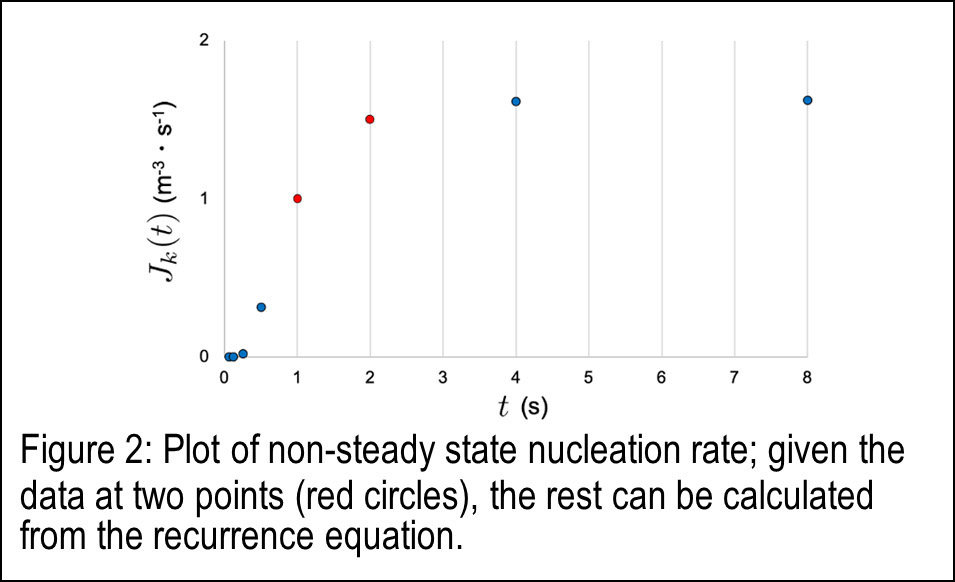
Theta functions also appear in physics, and I have been using them to study phenomena in applied physics. Non-steady state nucleation is a phenomenon such as that seen in the initial stage of vesiculation of carbonate water, which can be observed in daily life. This phenomenon is characterized by a quantity called the non-steady state nucleation rate Jk( t ). Measuring this quantity may require a long experiment, which presents a cost challenge. On the other hand, it was pointed out in 1969 that Jk( t ) is expressed by an elliptic theta function, but since its publication, there were no research utilizing the properties of theta function. In this study, nontrivial recurrence equations satisfied by Jk( 2nt ) were derived using the properties of theta functions, allowing the value of Jk( t ) to be estimated with a small amount of data (Fig. 2). The results can be used to reduce costs in experimental studies of non-steady state nucleation.
Blueprints for 4D Figures: Visualizing the Invisible Dimension

HAMADA, Noriyuki
Degree: PhD (Mathematical Science) (Kyushu University)
Research interests: Low-dimensional Topology, Mapping Class Groups of Surfaces, Symplectic Topology
I am researching a field of pure mathematics called low-dimensional topology. More specifically, there is a theory of “drawing” 4-dimensional figures on surfaces, and I am fascinated by the strong interplay between these 4D world and 2D world.
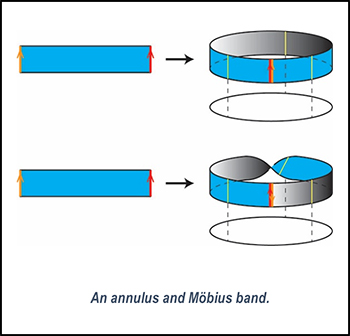
Before delving into the explanation of how to draw 4 dimensions, let’s first look at a simplified model with reduced dimensions. Consider a long rectangular strip and connect both ends, as shown in the following figure. There are two ways to connect them: in one way, a normal loop (called an annulus) is formed, and in the other way, a twisted loop (known as a Möbius strip) is created. Now, we place a hypothetical circle under the annulus and Möbius strip respectively, as shown in the figure, then it can be observed that there is a structure in which a short line segment is arranged above each point on the circle. In essence, lines (1D) are arranged over a circle (1D), resulting in an overall 1+1 = 2D figure.
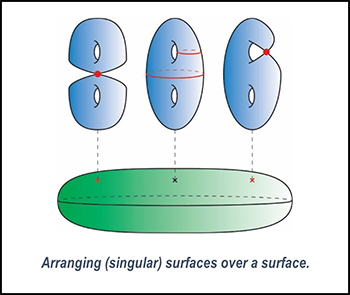
Expanding upon this line of thinking with imagination, one can conceive a space where surfaces (2D) are arranged over another surface (2D). The dimension of this space becomes 2 + 2 = 4D. Furthermore, by relaxing the conditions a bit more and allowing for surfaces above to have occasional singular points, as depicted in the following figure, it becomes possible to handle a very rich class of 4-dimensional objects (referred to in technical terms as symplectic 4-dimensional manifolds).
The surfaces arranged above are referred to as fibers. By drawing closed curves corresponding to singular points on a fiber, a “blueprint” that encompasses all the information of the envisioned 4-dimensional manifold can be obtained. More precisely, this blueprint is described in terms of a group called the mapping class group associated with the fiber surface.
In this way, there is a complementary study where 4-dimensional manifolds and the mapping class groups of surfaces are interconnected. For example, from the constraints of 4-dimensional manifolds, properties of mapping class groups have been derived, and conversely, discussions on mapping class groups have yielded properties of 4-dimensional manifolds.
My expertise lies in creating such “blueprints” within the mapping class groups. I have discovered foundational examples, crafted reusable and practical blueprints, and then constructed elaborate blueprints based on them, which established previously unknown 4-dimensional manifolds.
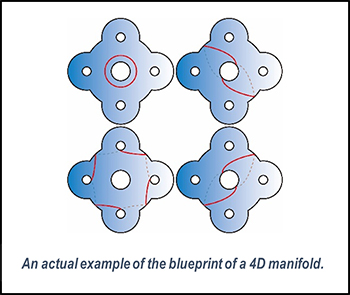
By the way, in the classification of 4-dimensional manifolds, there are two perspectives: the homeomorphic stance, where two manifolds are considered the same when they can be transformed into each other “continuously,” and the diffeomorphic stance, where they are considered the same when they can be transformed into each other “smoothly.” The distinction between these two approaches is highly subtle and is a central topic in 4-dimensional topology. In my recent study with a collaborator, we have discovered many 4-dimensional manifolds that are homeomorphic to certain standard 4-dimensional manifolds but not diffeomorphic. This has provided new insights into the gap between homeomorphism and diffeomorphism in 4D topology.
Algebraic topology and applied topology

KAJI, Shizuo
Degree: Doctor of Sciences (Kyoto University)
Research interests: Topology, Lie Groups, Applied Mathematics
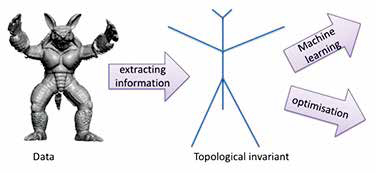
My main research interest is in the areas of topology. In addition to so-called “pure maths” problems, I work on various problems to which the methodology of topology applies. For example, I am interested in topological data analysis, an emerging interdisciplinary field in which topologists and data scientists work together.
Topology is a study of shapes and their deformation. As is often said, in topology a mug and a doughnut are not distinguished; they both have a “hole” and can be “deformed” to one another. Topologists do not care length, area, or angle but do care the numbers of connected components and holes of a shape. One of the main goals in topology is to assign numbers (or more generally, some algebraic objects) to shapes (topological spaces) which do not change under continuous deformation. These topological invariants tell the nature of the shapes and provide a way to distinguish and classify them. My specialty is in exploiting symmetry of the space to compute topological invariants such as cohomology and homotopy groups. Symmetry is usually encoded in the action of a Lie group on the space and it often reveals a beautiful connection between topology and combinatorics.
Looking at things in a topological manner is in fact close to how we view the world. As opposed to machines, which are very sensitive to subtle changes, we humans perceive things less accurately. But this enables us to recognise things robustly in a noisy environment. To extract information from big data, details are not so important and should be discarded to have a perspective view of the data. By the rigorous mathematical language of topology, we could teach a machine how to see things like a human. One such example is to use homology in data analysis. Homology captures “holes” of a space, and can be computed efficiently by a computer. The technique is successfully employed in clinical medicine, neuroscience, chemoinfomatics, and so on.
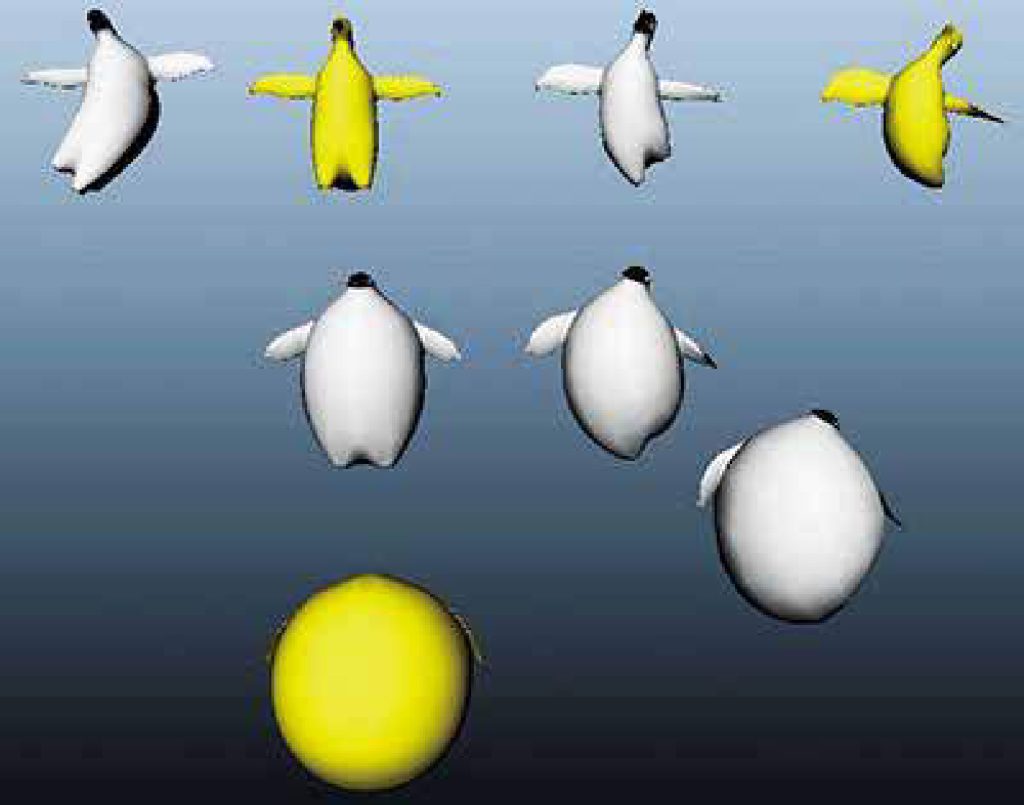
Aside from data analysis, perhaps a more direct application of topology is in handling shapes. Just as we can deform a mug to a doughnut, we may think of interpolating shapes. The figure below shows my computation with penguins. It looks fun but at the same time it can have serious applications in designing and optimising shapes.
Mathematics for materials structure analysis

Oishi-TOMIYASU, Ryoko
Degree: PhD (Mathematical Sciences) (The University of Tokyo)
Research interests: Applied Algebra/Number theory, Mathematical Crystallography, Algorithm
The research for materials structure analysis includes algorithm development based on harmonic analysis, signal processing, optimization and statistics, but I often obtain new findings by combining these with ideas and techniques in pure mathematics including algebra and number theory.
The following focuses on my three projects that have resulted in patents.
(1) CONOGRAPH method for ab-initio indexing (lattice determination)
”Ab-initio” means an analysis that does not use any prior information on the material structure (in this case the crystal lattice). After publishing papers about fundamental algorithms for the analyses listed below, I released programs for powder diffraction[1] and electron back scattering diffraction[2] far with the support by a lab of KEK I belonged to, and Nippon Steel Corporation.
・ Determination of lattice symmetry (Bravais lattice) under large observation errors … Application of lattice-basis reduction theory
・ Peak search
・ Figure of merit for finding solutions that fit experimental data well
・ General rules of forbidden reflections (described using topographs)
・ Method to detect ambiguity (uniqueness of solutions) … Application of arithmetic theory of quadratic forms
The software CONOGRAPH enhanced the success ratio in ab-initio indexing. The obtained results can be applied to various lattice-determination problems from diffraction data.
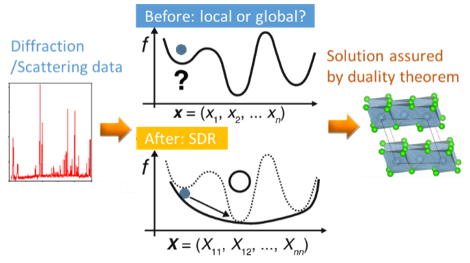
(2) Semidefinite programming relaxation (SDR) to ensure the global optimality
Local minimum is a well-known problem in nonlinear optimization. SDR is a method to obtain the global minima of quadratic optimization problems (QP) in a guaranteed situation (Fig.1). In general, phase retrieval to determine the amplitudes of the Fourier transform of the crystal structure (=structure factors) can be expressed as a QP.
This study was originally started to investigate the uniqueness of solutions in ab-initio crystal structure determination, but a useful application in magnetic structure analysis was found in a joint work with experimental scientists[3].
(3) Golden angle method for general surfaces and dimensions
The generalization of the golden angle method used for modeling phyllotaxis and sunflower heads has been an open problem addressed in various literature. We succeeded in the generalization by attributing it to a problem in geometry of numbers known as “product of linear forms”.
We’re now investigating how the developed method and ideas can be applied to modeling, pattern generation and mesh generation.
[1] https://z-code.kek.jp/zrg/
[2] J. Appl. Cryst. (2021) 54 (2), 624-635
[3] Scientific Reports (2018) 8:16228.
Topological Data Analysis and Machine Learning

Keunsu KIM
Degree: PhD (Mathematics) (POSTECH)
Research interests: Topological data analysis, Topological optimization
My primary research interest lies in the intersection of Topological Data Analysis (TDA) and Machine Learning (ML). In particular, I am currently focused on topological optimization.
Topology is the study of continuous objects, known as topological spaces, and the properties that remain invariant under continuous deformation. One of the most well-known invariants is homology, which quantifies the “holes” in a space and can be efficiently computed using linear algebra.
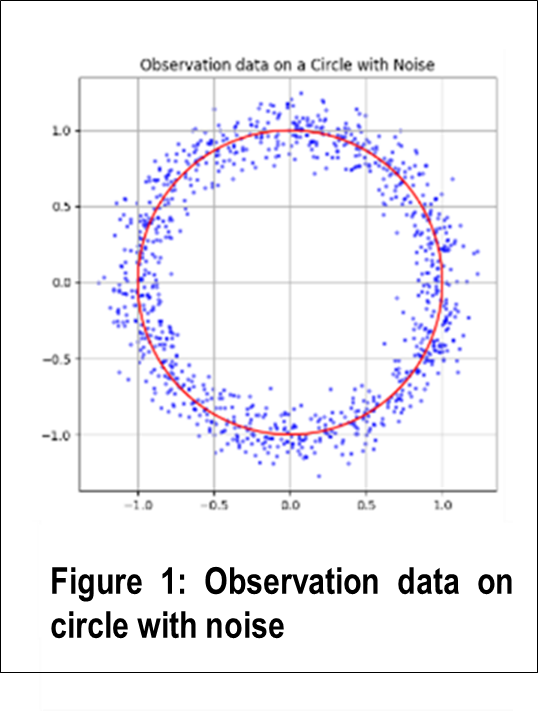
However, a fundamental challenge in data analysis is
that real-world datasets are inherently discrete and
lack meaningful topological properties. For instance,
in Figure 1, the observed data (blue points), sampled
from a red circle, do not form a continuous structure.
The goal of TDA is to infer the underlying continuous
shape (the population manifold) from these discrete
observations.
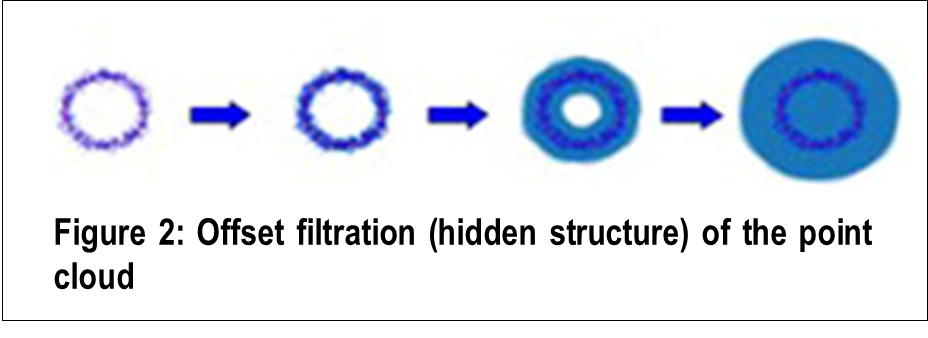
Traditionally, metric information has been used to construct hidden structures from data through methods such as offset filtration (Figure 2) or Vietoris-Rips filtration, and by analyzing these structures, one can infer the underlying continuous shape. It is known that if data is sufficiently and uniformly sampled from a manifold, observing the changes in homology at each step in the hidden structure (persistent homology) allows us to infer the homology of the original manifold.
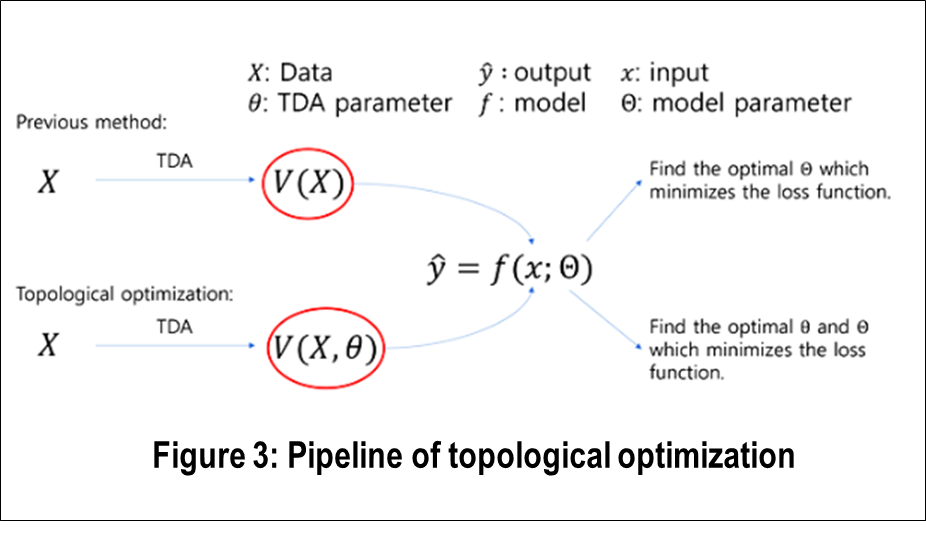
Since the 2020s, interest in topological optimization has grown, with ML playing a crucial role in the TDA process to better capture data characteristics. As shown in Figure 3, the ML model f includes the TDA parameter θ. This emerging paradigm enables a more flexible and data-driven approach to extracting topological information more effectively.
I am currently conducting research on topological optimization, exploring topological regularization in Nonnegative Matrix Factorization (NMF). NMF is one of the linear dimensionality reduction methods used to extract latent features (basis vectors) from a dataset. However, standard NMF does not explicitly capture the structural or topological properties of the data. My research focuses on applying topological regularization to NMF to extract latent features that preserve topological characteristics, such as connectivity and the presence of holes. The goal is to obtain more interpretable latent features from the dataset, enhancing the structural understanding of the extracted components.
Sparse Multivariate Analysis via L1 Regularization

HIROSE, Kei
Degree: PhD (Functional Mathematics) (Kyushu University)
Research interests: Sparse estimation, L1 regularization, Multivariate Analysis
Recently, the analysis of big data has becoming more and more important. Although the data volumes are increasing, most of the data values can be meaningless. Therefore, it is important to extract meaningful information from the big data. The sparse estimation, such as L1 regularization, is one of the most efficient methods to achieve this. The sparse estimation makes most of the parameters exactly zeroes. The meaningful variables correspond to the nonzero parameters. A remarkable feature of the L1 regularization is that even if the number of parameters is several millions, it takes only several minutes to compute the solution. In addition, the L1 regularization has many good statistical properties. For these reasons, many statisticians are interested in the L1 regularization.
I am interested in multivariate analysis via L1 regularization. Multivariate analysis investigates a relationship among variables by some procedure such as aggregating several variables. The multivariate analysis has been widely used for several tens of years. I am interested in factor analysis, which is one of the most popular multivariate analyses. Conventionally, the factor analysis has been used in psychology and social sciences, but recently it has been used in life science and machine learning. The factor analysis has been becoming more and more important in many research areas. In the following, I introduce two recent results related to factor analysis.
(1) Sparse estimation in factor analysis
An interesting fact of the factor analysis is that the factor loadings have a rotational indeterminacy, that is, the loading matrix is not unique. In factor analysis, we estimate parameters by using rotation technique. This kind of technique may not be used in any other statistical models. The rotation technique has been widely used in factor analysis for more than 50 years.
I applied the L1 regularization to factor analysis model and compared the L1 regularization with the rotation techniques.
Then, I found a very interesting fact: the regularization is a generalization of the rotation technique, and the regularization can achieve sparser solutions than the rotation technique. Furthermore, I developed an efficient algorithm for computing the entire solutions, and made an R package fanc (https://cran. r-project.org/web/packages/fanc/index.html). There exists papers that use the fanc package.
(2) Maximum likelihood estimation in factor analysis for a large number of missing values
In some cases, the data values can be missing. For example, when a questionnaire asks a research participant about a feeling towards another person, many questions are prepared in order to investigate their impressions, using a wide variety of personalassessment measures. However, answering all of the questions may cause participants fatigue and inattention. In order to gather the high-quality data, the participants may be asked to select just a few of questions; this leads to a large number of missing values.
When the data values are missing, we can use a standard EM algorithm to estimate parameters. However, when a majority of data values are missing, the ordinary EM algorithm is extremely slow. In order to handle this problem, I modified the EM algorithm. I found that the modified EM algorithm is several hundreds or thousands times faster than the ordinary EM algorithm.

Finite mixture models for statistical inference

Hien Duy NGUYEN
Degree: PhD, University of Queensland, Australia
Research interests: Mathematical Statistics, Statistical Computing, Statistical Learning, Bayesian Statistics, Signal Processing, Stochastic Programming, Optimization Theory
Many real-world datasets are heterogeneous and multipopulational phenomena. In such contexts, it is insufficient to capture the overall variation among the data using a single statistical model. Therefore, a cohesive approach to modeling the multiple subpopulations within the superpopulation is necessary. In such scenarios, a useful approach involves modeling each subpopulation and their contributions to the superpopulation through a weighted averaging construction, known as a finite mixture model. These models are highly flexible and interpretable, enabling them to capture and provide inference for known heterogeneities in the data while also identifying new heterogeneous phenomena that were previously concealed.
The class of finite mixture models is extensive, and choosing between different mixture models can be challenging. In my work, I have studied model selection procedures required to make mathematically principled choices among competing finite mixture models. I have made progress in two key directions to address this problem. Firstly, I employ sequences of hypothesis tests to determine the number of components or subpopulations required in each mixture model. This approach relies on a new hypothesis testing method called universal inference, which offers a straightforward and assumption-light mechanism for deciding whether a model accurately represents the observed data. Using these universal inference tests, I have developed a way to construct confidence intervals for the number of underlying subpopulations in the data, providing insight into the complexity of the overall superpopulation.
Secondly, by leveraging modern stochastic programming techniques for optimizing random objects, I have developed new penalization methods for selecting between different finite mixture models within broader model selection and decision problems. My novel information criterion, known as PanIC, offers a more assumption-light alternative to existing methods like the Bayesian information criterion or Akaike information criterion. PanIC provides a single-number summary for choosing between competing models, guaranteed to asymptotically select the correct model as the dataset size increases.
Beyond their utility for modeling heterogeneous processes, finite mixtures and their regression variants, the mixture of experts (MoEs) also serve as excellent functional approximations of probability density functions (PDFs) and conditional PDFs that characterize statistical relationships. My colleagues and I have contributed to understanding the approximation theoretic properties of mixture models and MoEs for various classes of PDFs. We have provided sufficient conditions for ensuring that PDFs, conditional PDFs, or mean functions of conditional PDFs can be effectively approximated using a sufficiently large number of components in a finite mixture model construction. These results, often referred to as universal approximation theorems, are valuable for determining whether a class of functions serves as an adequate basis for modeling an underlying mathematical phenomenon.
My research in mixture model computation, estimation, and inference has found widespread application in real-world scenarios. For example, I have collaborated with neuroscientists and cell biologists to analyze heterogeneous biological phenomena, worked with quantum physicists to characterize switching behaviors of quantum circuitry, assisted economists in characterizing subpopulations of experimental outcomes, partnered with civil engineers to study regional differences in traffic behavior, supported fisheries scientists in characterizing growth stages of aquatic species, and collaborated with image scientists to segment and characterize imaging data, among other practical applications.
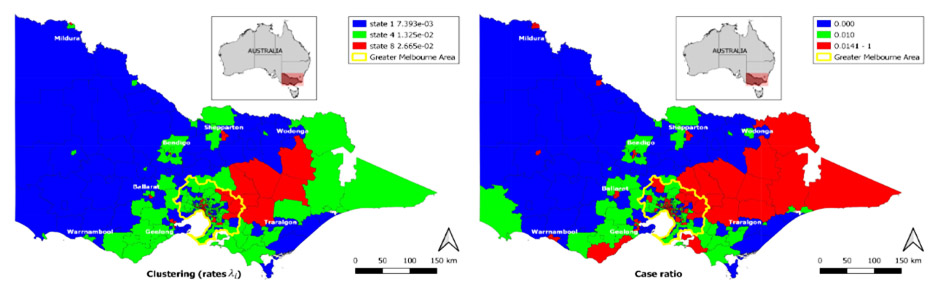
Figure 1: Traffic crash rate clustering of different regions in Victoria, Australia.

Figure 2: Quantization of mandrill photograph using different mixture models.
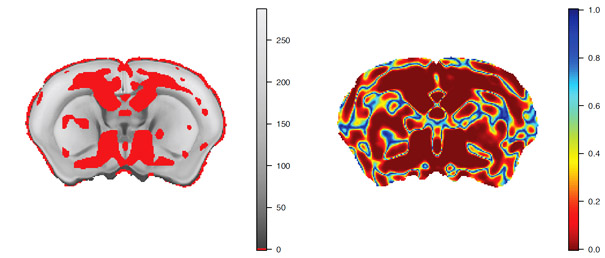
Figure 3: Mixture-based false discovery rate control of p-values for a mouse brain morphometry experiment
Bridge between measurements and mathematical modeling via Bayesian inference

Satoru TOKUDA
Degree: PhD (Science) (the University of Tokyo)
Research interests: Research Interests: Bayesian inference, modeling, statistical mechanics
As highlighted by Kepler’s laws of planetary motion since the 17th century, mathematical modeling that describes observed data using simple formulas has deepened our understanding of various physical phenomena. However, observed data are often beyond our understanding in modern science, which makes full use of advanced measurement technologies to capture more complex phenomena. My grand challenge is establishing principles of modeling rooted in observed data to provide guidelines for understanding all phenomena without ambiguity. I am exploring the mathematics of a statistical method called Bayesian inference and promoting empirical research through collaboration with researchers from a wide range of natural sciences focused on condensed matter physics. Through my research to date, I have focused on the following three issues that can make data difficult to understand.
(1) Model uncertainty
Models represent the essence of a phenomenon, but the essence is not always obvious. In many cases, the decision relies on the researcher’s insight, and they sometimes differ in opinion. For example, the vibration phenomenon shown by the observed data in Figure 1 can be modeled by a function that represents simple harmonic motion if friction can be ignored or damped vibration if not, while which is more appropriate depends on the situation.
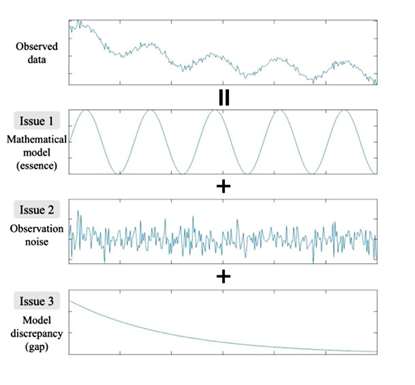
observation noise, and model discrepancy.
We are conducting empirical research to resolve such uncertainties using Bayesian inference, which quantifies the validity of each model against observed data as a probability. We have shown that our approach is useful for selecting models in condensed matter physics, such as velocity distribution functions and band structures.
(2) Observation noise
Measurements involve the observation noise. The parameter values estimated from more noisy data are more uncertain. Focusing on the fact that such an error propagation also affects model evaluation, we have developed a methodology to estimate the noise level and the valid model jointly. We also demonstrated its usefulness through empirical research. Estimating the valid model and its parameter values depends on the noise level (data quality) and data amount. By proceeding with theoretical analysis based on the correspondence between Bayesian inference and statistical mechanics, we have elucidated the scaling law for Bayesian inference depending on the quantity and quality of the observed data.
(3) Model discrepancy
There is always a gap between ideal and reality, that is, between model and observed data. First, a model is an approximate representation of the truth. Additionally, observation noise and systematic errors occur between the truth and the data. Collectively, I refer to everything other than random noise as the model discrepancy. Attributing the origin of model discrepancy is difficult, and it is even more challenging to describe them in concrete formulas. Besides, the traditional asymptotic theory only justifies Bayesian inference by assuming an ideal situation without model discrepancy. Through empirical research, we are developing a methodology to deal with model discrepancy systematically and trying to construct a novel asymptotic theory of Bayesian inference to support its validity.
Small Area Statistical Inference and its Application

HIROSE, Masayo
Degree: PhD (Engineering) (Osaka University)
Research interests: Statistical Science, Small area estimation, Mixed effect model
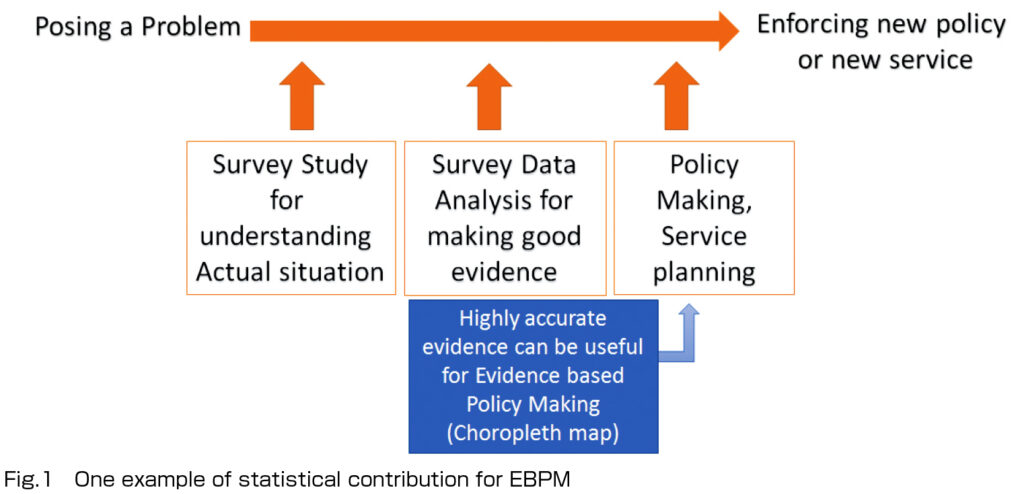
Recently, there is a growing importance of Evidence-Based Policy Making (EBPM). For estimating characteristic values of each small administrative division, the statistical model-based approach can get more efficiency of estimating method than the design-based approach. The concept of the model-based approach is “borrow strength from other areas” (Ghosh and Rao, 1994). That implies the approach can provide high-quality evidence for new policymaking or service planning. And also, it could contribute to solving some social problems (see Figure 1). Such statistical methodology has been accomplished the development especially in the research field of official statistics. Hereafter, we shall briefly introduce some of my researches about model-based approaches.
(1) Constructing Small Area Estimation Method
In estimating characteristic values of each small administrative division, model-based approach conduces the empirical best linear unbiased predictor under the assumed model, which minimizes the mean squared (prediction) error among any linear unbiased predictors in asymptotic sense. However, there are some practical issues of the existing empirical predictor still yet. Therefore, we have constructed a new statistical method which not only avoids a practical problem but also maintain efficiency in asymptotic sense. Moreover, we have addressed several issues for the development of confidence interval method for small area inference.
(2) Application to Survey Data
We are also interested in the application of our statistical method to real survey data to make high-quality evidence for EBPM. We already applied our model-based approach to Japanese consciousness survey data for understanding a consciousness trend of each small administrative division, like Cho-Chome. Moreover, we compared the approach with the conventional estimation method used in the Japanese public administrative research area. For more details, please see Hirose et al. (2018, JJSS/Japanese version)
On robust model selection criteria based on statistical divergence measures

KURATA, Sumito
Degree: Doctor of Science (Osaka University)
Research interests: Statistical Science, Model Selection, Robustness
In real data, there frequently exist some outliers (observations that are markedly different in value from others) derived from, for example, unusual abilities, catastrophe-level phenomena, or human errors. It is difficult to provide a clear definition or threshold of such outliers, moreover, it is effectively impossible to prevent their occurrence. Thus, robust methods that reduce the influence of outliers have a large significance. My research focuses on robust analytical methods, especially in the model selection problems. I focus on applying statistical divergence, a measure of farness between probability distributions, to examine the closeness of the underlying “true distribution” and models. When selecting a model, the robustness is a desirable property, but most model selection criteria based on the Kullback-Leibler divergence tend to have reduced performance when the data are contaminated by outliers. I have derived and investigated criteria that generalize conventional information criteria such as AIC and BIC, based on the BHHJ divergence, a divergence family that has robustness in parametric estimation.
Since outliers are distant from other observations, they often have a bad influence on values of estimates and model selection criteria. To discuss the robustness of a criterion, we need to evaluate the perturbation of it. In this field, we evaluate the sensitivity of an estimator against contamination, by exploring the difference between populations with and without outlier-generating distribution. We assume that most of observations are drawn from a (true) population distribution, and we can interpret that outliers are drawn from a probability distribution differing from the true distribution (Figure 1). I have investigated the robustness of criteria based on many divergence measures by evaluating the difference of its values between contaminated and non-contaminated data-generating distributions. Consequently, I verified that criteria derived from some class of divergence measures, such as the BHHJ divergence, have robustness in model selection (Figure 2). Since models can be created for all phenomena, it is significant to investigate “good” model selection criteria for all fields. By examining various properties that contribute to selection including robustness, I aim to conduct a research that can support a wide range of fields.
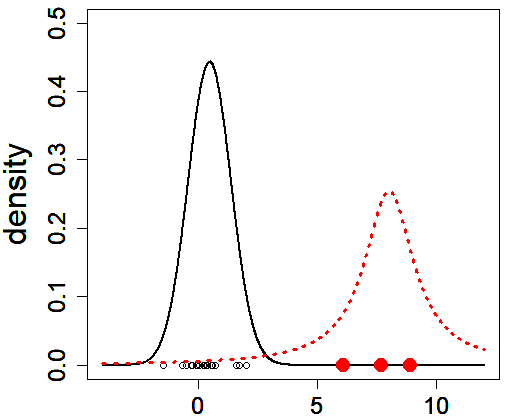
(Caption of Figure 1) We consider two distributions: the “true” population distribution (black curve) and another one that generates outliers (red), and we suppose that observations are drawn from the mixture distribution composed of the two distributions. If a result of analysis varies greatly depending on the presence of absence of outliers, the corresponding method is regarded as to be sensitive against contamination.
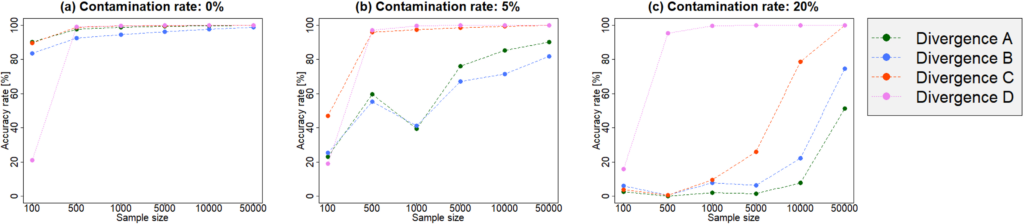
(Caption of Figure 2) Accuracy rates of model selection criteria based on some divergence measures (Divergences A-D) in a numerical simulation of selection problem of the generalized linear model, for different sample sizes and contamination rates. Criteria based on Divergence A and B are sensitive against outliers. In contrast, we can see that Divergence D has strong robustness against contamination of data-generating distribution.
Intertwining Mathematics and Cryptography

NUIDA, Koji
Degree: Ph.D. (Mathematical Sciences) (The University of Tokyo)
Research interests: Mathematical Cryptography, Secure Multiparty Computation, Combinatorial Group Theory
Information technology, such as secure internet shopping, is nowadays a ubiquitous tool for our convenient daily life, and cryptography is one of its main underlying indispensable technology. And also, mathematics is playing a fundamental role in cryptography. The RSA cryptosystem invented at the end of 1970s is based on properties from elementary number theory. The so-called elliptic curve cryptography invented around the middle of 1980s is (as the name suggests) based on properties of elliptic curves. Moreover, post-quantum cryptography, a kind of newgeneration cryptosystems for the forthcoming era with development of quantum computers, is further based on several mathematics such as linear algebra, Gröbner basis, high-dimensional integral lattices, etc.
Mathematicians can enjoy cryptographic research by “making use of various, state-of-the-art mathematics” of course, but further by “achieving advanced work by cleverly utilizing even elementary tools” and by “exploring good definitions for several cryptographic notions in both intuitively natural and theoretically convenient ways”.
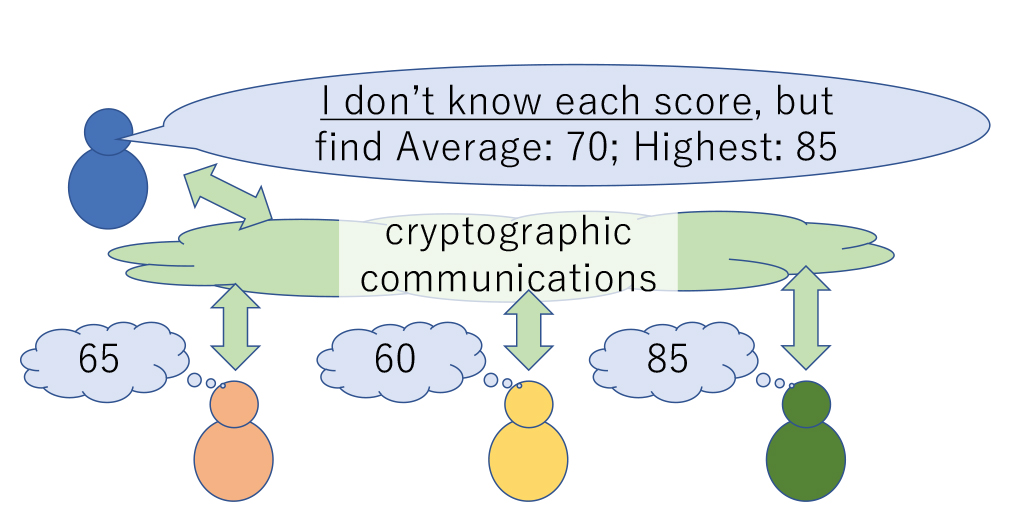
My main interest in cryptography is with “secure computation”. Secure (multiparty) computation is a kind of “magical” technology that enables necessary information processing on many users’ input data while keeping their individual input data secret to each other. Among standard mathematical and cryptographic tools for secure computation, “fully homomorphic encryption” (FHE) is a special kind of encryption by which the original data inside given ciphertexts can be processed without decrypting the ciphertexts. In our proposed FHE scheme (presented at international conference EUROCRYPT 2015), a major ingredient was the following algebraic property: any function over a finite field admits a polynomial expression. This property itself is in fact an elementary fact, and it is a typical episode showing that even elementary mathematics can yield a significant cryptographic work when properly used.
There is a certain complicated operation unavoidable in the existing constructions of FHE, which has been a major bottleneck towards efficiency improvements. One of my recent research challenges is to remove this operation by using group-theoretic approaches not used in the previous research. I am expecting that combinatorial group theory, which is my main expertise in mathematics, might also be applicable to this subject, which gives me further motivations for the research.
As other recent result on secure computation with “mathematical” flavor, I found a “pathological example” showing that an “intuitively reasonable” known construction methodology that had widely been regarded secure is in fact not always secure (presented at international conference PKC 2021).
Cryptography (as well as other research areas) is really related to various mathematics. I myself have also encountered several surprising situations where some mathematical topic has an unexpected application to cryptography. I would also like to make such connections between mathematics and cryptography more popular.
Security analysis on Post-Quantum Cryptography

IKEMATSU, Yasuhiko
Degree: PhD (Mathematical Science) (Kyushu University)
Research interests: Post-Quantum Cryptography, Multivariate Public Key Cryptosystem
RSA and Elliptic Curve Cryptosystems (ECC), which support modern information security, are constructed based on the hardness of integer factorization problem and discrete logarithm problem. However, if a large-scale quantum computer is built, then these problems can be solved in polynomial time by Shor’s algorithm and its variant, it means RSA and ECC will be vulnerable any longer.
Post-Quantum Cryptosystem (PQC), which resists against quantum computer attacks, is being researched all over the world because of the above-mentioned reason. PQC requires research to deal with various mathematical problems different from integer factorization and discrete logarithm problems. It is necessary to use various mathematical theories beyond elementary number theory.

My research interest is on PQC, especially, Multivariate Public Key Cryptosystem (MPKC), constructed based on the (MQ) problem of finding a solution to Multivariate Quadratic equations over a finite field. Since it is proven to be NPcomplete, it is expected that MPKC is resistant to quantum computer.
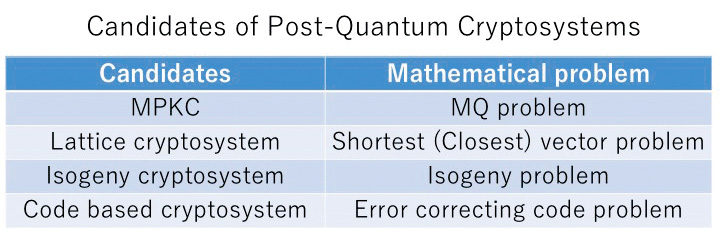
The virtues of MPKC are high-speed performance and its small signature size among other candidates. Therefore, MPKC is suitable for smart cards and IoT devices. There is also an interesting trial of creating crypto currency from an MPKC signature scheme, Rainbow, in recent.
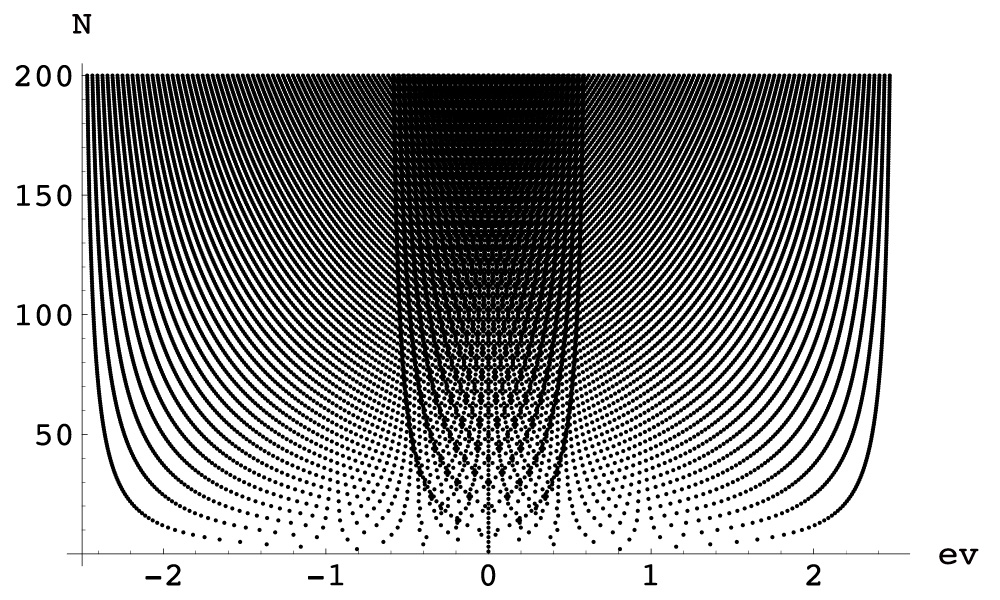
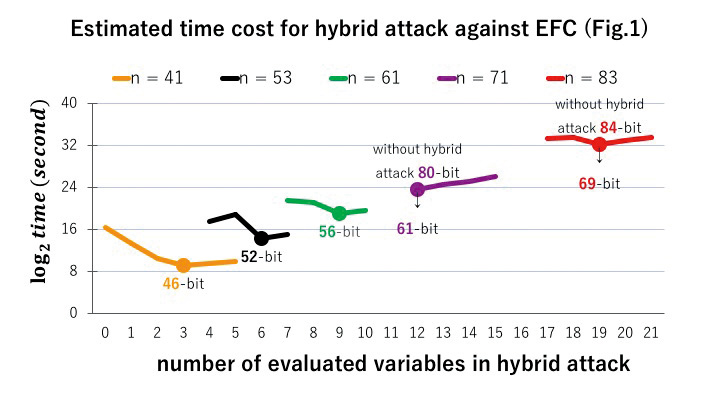
I mainly study security analysis on MPKC. Mathematical arguments with respect to Gröbner basis or algebraic geometry are necessary. However, the complexity analysis against Gröbner basis algorithm, especially, F4/F5 algorithm is still not theoretically clear. Its complexity analysis depends on experimental results. For EFC MPKC encryption scheme, I am curre-ntly working on, I experimentally found that its security is weaker against hybrid attack than original estimation (Fig.1). However, its theoretical explanation is not yet established and remained as an open problem.
I also study other PQC, as lattice and isogeny cryptosystems. I am interest-ed in constructing a new cryptosystem by combining them.
“Weird” = “Honest”

MATSUE, Kaname
Degree: Doctor of Science (Kyoto University)
Research interests: Dynamical Systems, Numerical Analysis (Rigorous Numerics), Singular Perturbation Theory, Combustion, etc.
Many natural phenomena, such as the motion of objects, the flow of air, or the temperature of objects or spaces, are described by solutions to differential equations. Typically, the solutions gradually approach stationary states (described by constants, time-periodic oscillating functions, etc.) or diverge exponentially, but occasionally there are “singular” behaviors that do not fit into this framework. For example, for u’ = u2 (prime is the time derivative), if we take the values of u at time t=0 positive, the solution goes to infinity at t→T for some finite value of T, and the equation becomes “unsolvable” thereafter.
This is a “weird” behavior that cannot occur in typical physical phenomena and is called a “finite-time blow-up” of the solution. Finite-time blow-ups are often identified as mathematical objects of peculiar phenomena, such as thermal runaway associated with heat source ignition. On the other hand, like the above equation, the system itself is often nonsingular, and for a given system, questions “does blow-up occur?” and if so, “when, where, and how?” are nontrivial to answer, and control of such behavior requires a deep understanding of the phenomenon itself. Meanwhile, we are dealing directly with “infinity” for blow-up, which is difficult to capture mathematically and numerically, and this phenomenon itself has been the subject of mathematical research for many years.
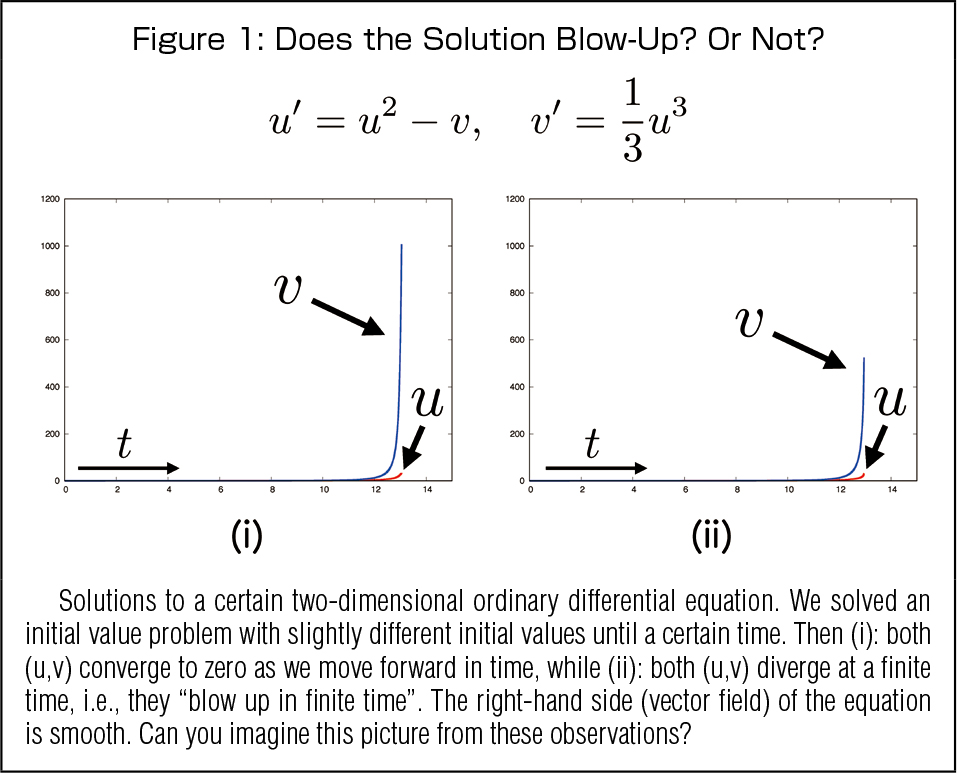
One of my research themes is to realize a unified description of “weird behavior” such as blow-ups in a standard way. One concrete idea is to “embed the entire space in a hemisphere or cut paraboloid and represent infinity as its boundary”. This is analogous to the Riemann sphere in Complex Function Theory and compactification in Topology, but here we also pay attention to the scalability of the system, construct an embedding of the entire space in an appropriate (bounded) surface, and express infinity as the boundary: the “horizon”. This idea originates from the way singularities and infinity points are viewed in algebraic geometry. Combining it with dynamical systems theory, which comprehensively describes the possible (qualitative) behavior of all solutions, we obtain the correspondence “Divergent Solutions = Those approaching to sets on the horizon”. Furthermore, the way the solution converges to the horizon makes it possible to accurately describe the blow-up behavior. This is achieved by combining geometric aspects of dynamical systems, algebraic geometry, and asymptotic analysis.
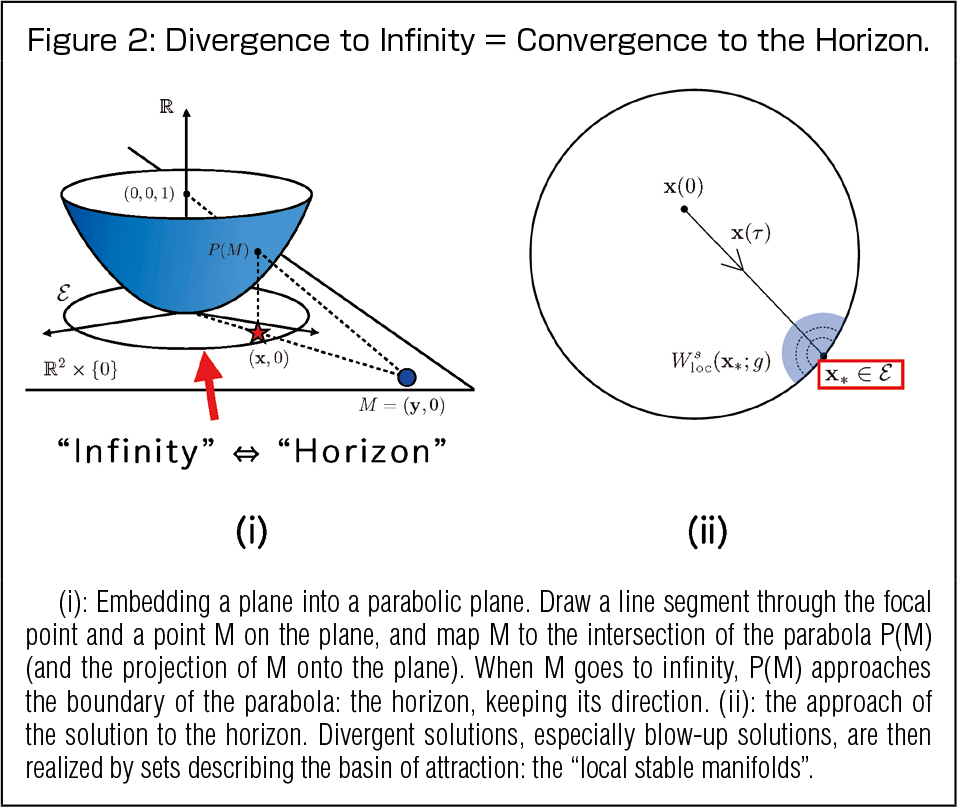
One advantage of this approach is a big compatibility with other theories and techniques, such as numerical analysis; (1): the behavior of the solution is covered, including the presence or absence of blow-ups; (2): blow-up solutions broken by perturbations of initial values are computed numerically with mathematical rigor; and (3): even “complex” blow-ups can be accurately captured through the horizon. These can be achieved by combining rigorous numerics, singularity theory, etc.
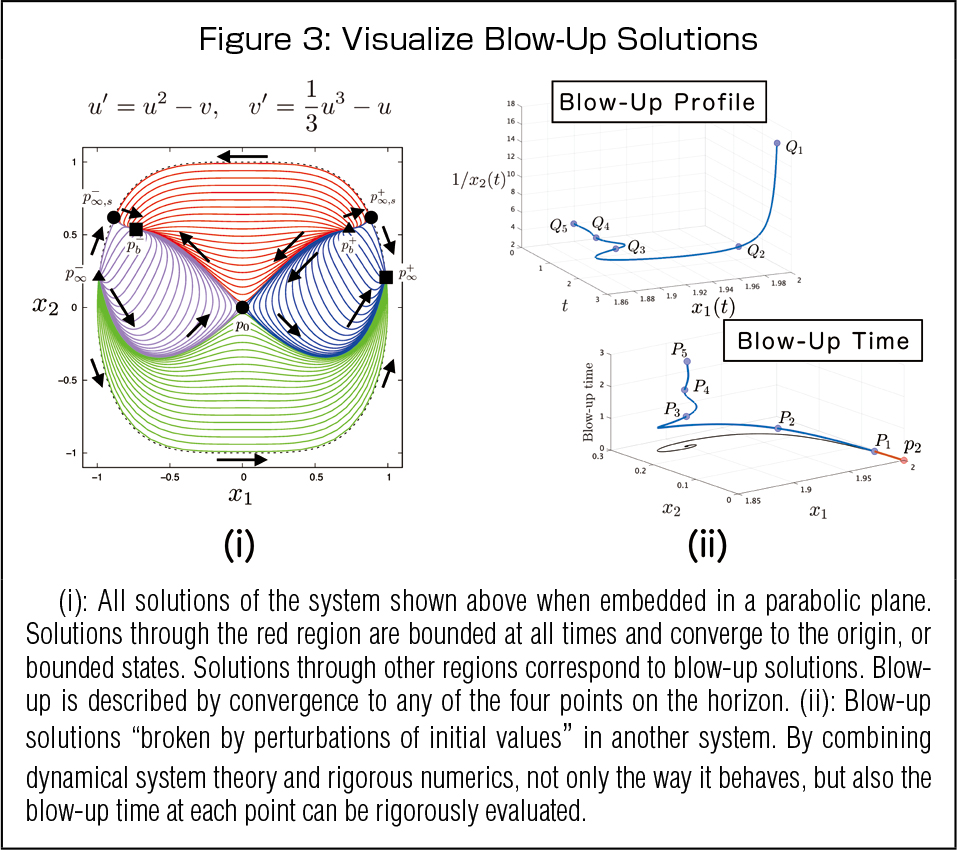
Not only blow-ups, but also various “finite-time singularities” are difficult to characterize. However, by changing the way of looking at it as described above, it is gradually becoming clear that it is actually just a straightforward behavior seen from a different viewpoint. This way has been applied to multiscale dynamics in the past, and more recently to tipping points, which can also be “interpreted in a straightforward manner” with knowledge of dynamical systems theory and geometry. The idea of describing these in a comprehensive manner will lead to the view that “weird” = “honest” in many respects.
Explainable AI through Waveform Patterns

Akihiro YAMAGUCHI
Degree: PhD(Information Science)(Nagoya University)
Research interests: Machine Learning, XAI, Time-series Data Mining, Interpretability
My main research interests are in the area of explainable machine learning and time-series data mining, with applications to the infrastructure and manufacturing sectors. In these industries, challenges beyond AI’s predictive accuracy often arise:
C1. → Field experts are knowledgeable in waveforms and seek transparency in AI decision-making.
C2. → Equipment typically operates normally, making it difficult to collect anomalies.
To address these industrial challenges, we have been proposing and developing machine learning methods that discover local waveform patterns used in AI decisions. Two approaches are introduced below:
(1) Shapelet Learning
In data mining and machine learning, automatic classification of time-series data (e.g., normal/abnormal) has been widely studied. Shapelet learning refers to jointly learning local and interclass-discriminative waveform patterns, called “shapelets,” and a classifier. This method is formulated as a continuous optimization problem in which the number of shapelets K and their length L are given in advance, the shape S is a K × L matrix, and S is found so as to minimize the classification error. This enables experts to interpret the AI’s decision rationales by associating shapelets with mechanical phenomena, such as loose screws causing faults, thereby addressing C1.
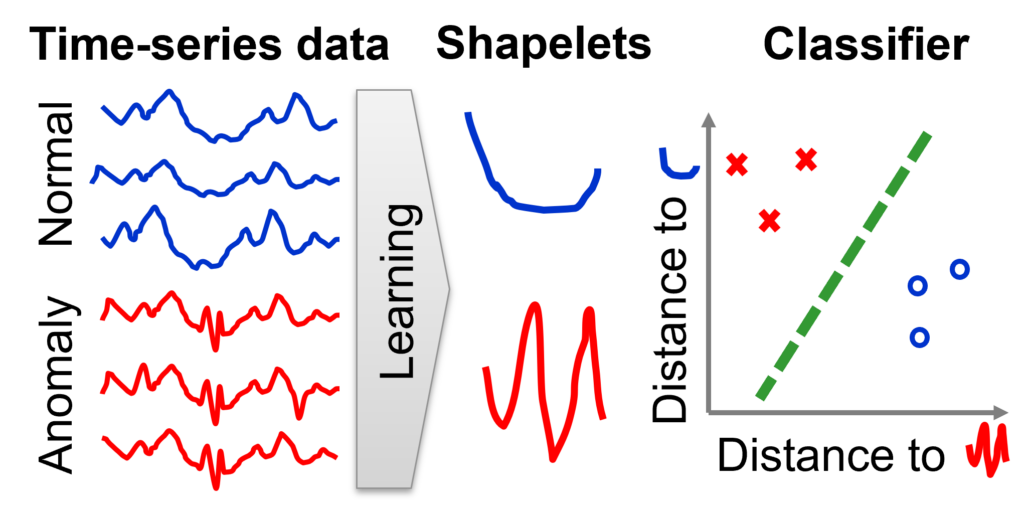
Learning shapelets for time-series classification
However, conventional methods require anomaly data for training, failing to address C2. To address both challenges C1&2, we developed an anomaly detection method that learns shapelets only from normal data and applied it to substation equipment. When examining the parts that most diverge from normal shapelets, we found slightly gentler slopes in anomalous waveforms, aligning with expert knowledge about equipment slowdown. This interpretability fosters experts’ trust in AI diagnostics.
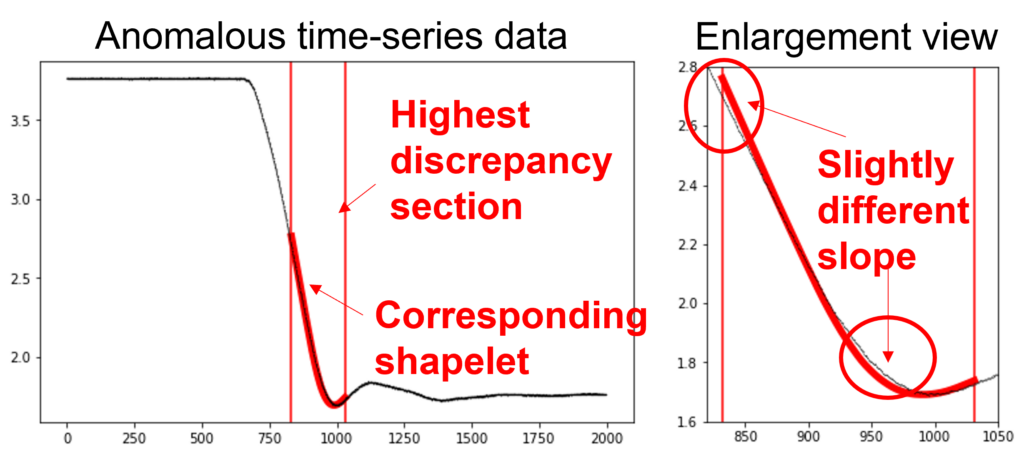
Decision rationale for shapelet learning when applied to substation equipment diagnosis
(2) Counterfactual Waveform Generation
While some black-box methods achieve high accuracy, we have also confirmed their accurate anomaly detection in our industries. This led us to explore XAI that separates decision-making and explanation methods for independent improvement. In particular, the counterfactual explanation can generate local waveform patterns that can be used as the AI’s decision (classification/anomaly detection) rationales, like shapelet learning. Applied to a substation equipment with anomaly involving delayed shock absorption, this method has generated counterfactual waveforms that matched expert assessments.
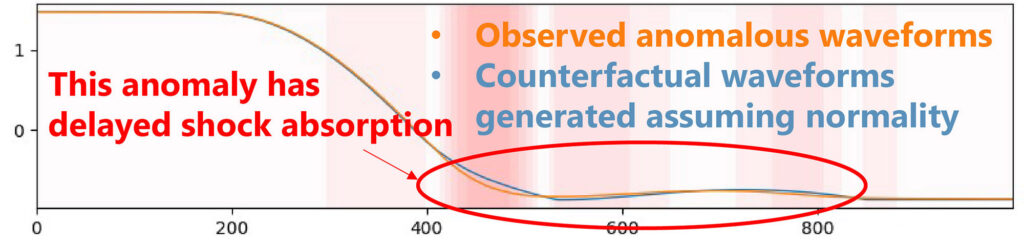
Decision rationale by counterfactual waveforms
Social Mathematics and Dynamic Optimization

KIRA, Akifumi
Degree: Doctor of Functional Mathematics (Kyushu University)
Research interests: Social Mathematics, Dynamic Optimization, Stochastic Optimization, Markov Decision Process
My main research field is mathematical optimization. I am particularly interested in problems that require repeated decision making (multi-stage decision processes) and problems involving uncertainty (stochastic models). I have been researching the theory and application of dynamic programming, which is a method to efficiently solve these kinds of problems. I am also engaged in research on social mathematics, which uses mathematical techniques to design fair and highly convincing systems and measures to address social issues. My co-researchers and I have developed technology in collaboration with real world sites of social issues. Two of these case studies are presented below.
The admissions process of matching children to daycare centers takes into consideration not only applicant priority criteria (i.e., each applicant’s childcare needs are calculated as a score.), but also requests for siblings to be admitted to the same daycare center. This is called “Matching with Couples” and is known to be a difficult problem even academically. Figure 1 shows two patterns of applicant dissatisfaction. An excellent seat assignment that does not cause this type of dissatisfaction is called “stable matching.” However even its existence is not guaranteed, and satisfactory adjustments are not easy to achieve.
(a) There is a child with a lower score at my first choice.
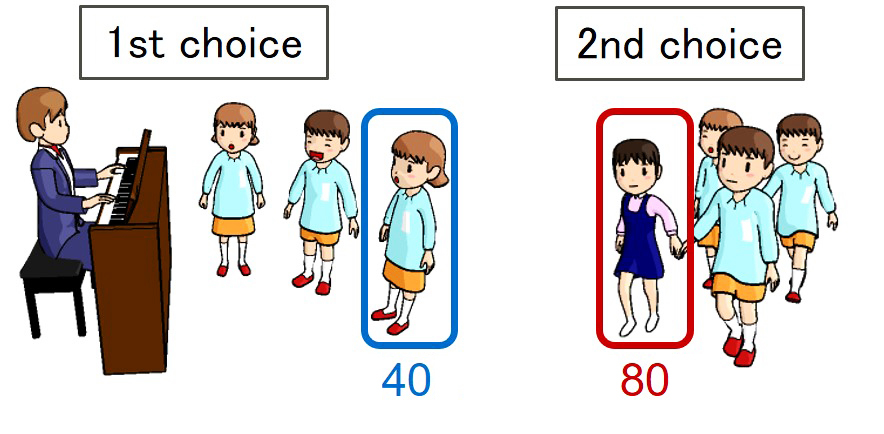
(b) Siblings should have been admitted together to their third choice.
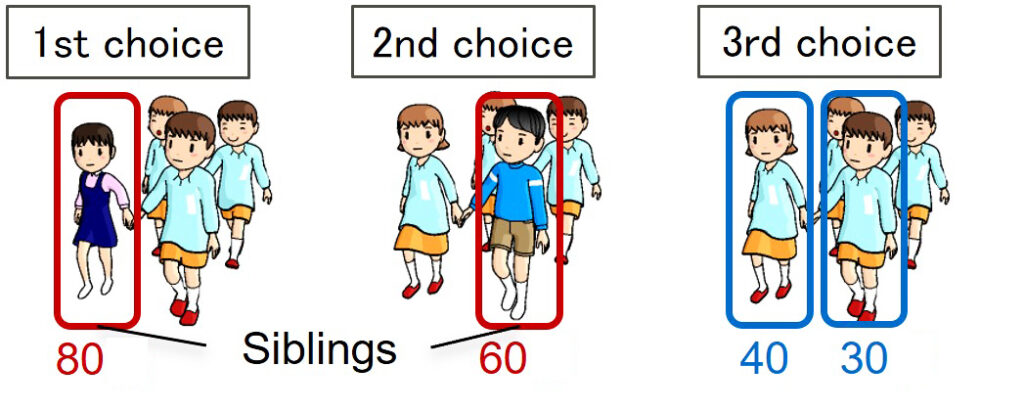
Figure 1: Patterns of dissatisfaction among applicants
As a result, each local government required a great deal of manpower and time for trial and error, and in some local governments, problems arose such as an increase in the number of cases where siblings were placed in separate daycare centers. Therefore, Division of Fujitsu Social Mathematics of IMI, together with Fujitsu Laboratories, addressed this issue and proposed a new method (using the theory of extensive form games) to achieve fair seat assignment. The proposed method has been commercialized by Fujitsu Limited and is already in use by 35 local governments as of June 2020.
The logistics industry in Japan is facing a severe shortage of labor, and there is an increasing need for joint transportation allowing large amounts of cargo to be transported using fewer trucks. Therefore, we developed a joint transportation matching technology that instantly lists and proposes combinations of highly efficient combined transportation using a database with many registered transport lanes. For example, round-trip and triangular transportation are effective in reducing the empty backhauls (Figure 2). The lower the empty running rate is, the more efficient the process is. However, browsing through enormous combinations of two transport lanes is time consuming. Therefore, our newly developed technology makes good use of the hidden inequalities, such as the “distance axiom,” to narrow down the search range without sacrificing accuracy. This technology has been installed as a core engine in the joint transportation matching system “TranOpt” provided by Japan Pallet Rental Corporation. As of October 2023, approximately 180 companies are using this system.
Figure 2: Processing a triangular transport matching request
Understanding Phenomena by Numerical Simulations

TAGAMI, Daisuke
Degree: PhD (Mathematical Science) (Kyushu University)
Research interests: Numerical Analysis, Computational Mechanics
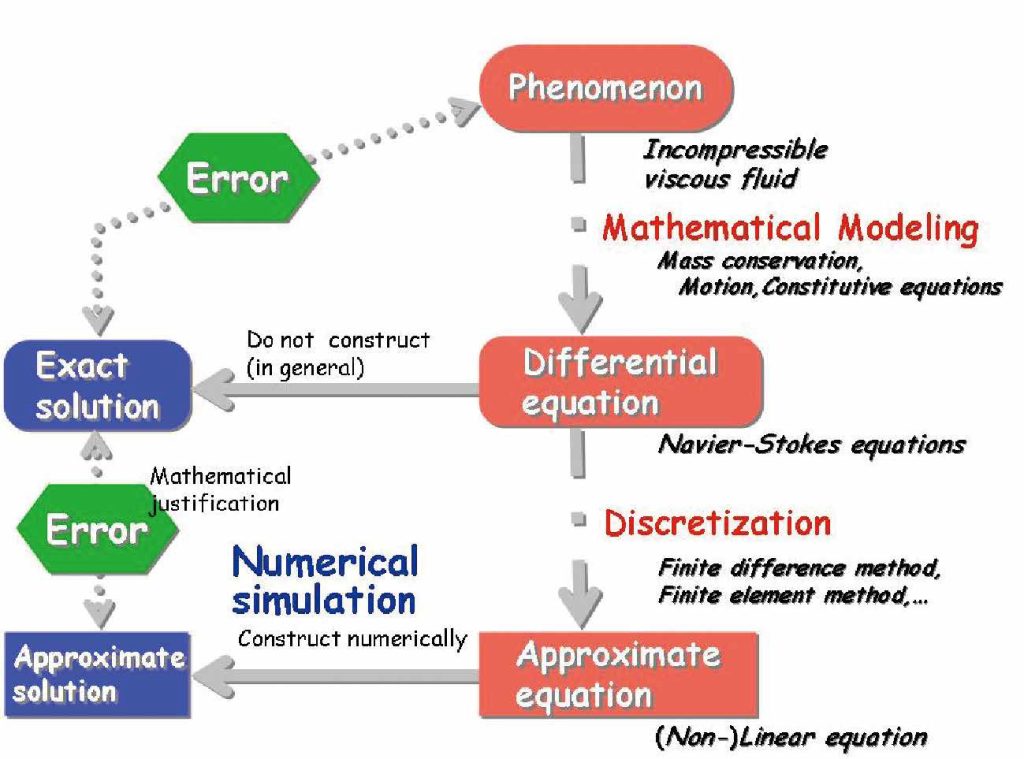
I am interested in understanding phenomena in nature and industry, for example, water flow in rivers and heat transfer in furnaces, by numerical simulations. The numerical simulation consists of three parts: mathematical modeling, discretization, and numerical computation; see Fig.1. First, in the mathematical modeling part, the phenomena are described by differential equations based on physical laws. Next, in the discretization part, the differential equations are approximated by linear systems, which can be handled with computers. Finally, in the numerical computation part, methods to solve the linear systems are implemented in computers to show the phenomena. I focus my attention to proposed numerical simulation methods and to justify the accuracy and efficiency of the methods mathematically. Moreover, I perform numerical computations of various practical problems by using the proposed methods, then I apply them for understanding the phenomena in nature and the design of industrial products.
One of my research projects is numerical simulation of the heat transfer phenomenon of glass raw material in melting glass furnaces; see Fig.2. Glass raw material, which is high temperature (about 1,500℃), is considered as an incompressible viscous fluid, so the phenomenon in the furnaces can be described by thermal convection equations with strongly temperature-dependent coefficients. By introducing the backward Euler method in time and the mixed consistent finite element in space, we have proposed numerical simulation methods for thermal convection equations, and have established optimal error estimates of them. Moreover, we have also proposed a numerical simulation methos for heat balance in the whole melting glass furnace, which is based on the consistent flux method. Due to the consistent flux method, we have established optimal error estimates, which imply mathematically that the computation of the boundary flux by the domain integral is more accurate than one by the boundary integral. Therefore numerical simulations based on the mathematically justified methods can be applied to determine the optimal design of melting glass furnaces, which maintains the quality of products and reduces the energy consumption.
Another research project is numerical simulations of magnetic field problems, for example, eddy current problems in transformers; see Fig.3. To obtain accurate numerical simulation results in cases of complicated domains and phenomena, we need to solve linear systems effectively in the numerical computation part , whose number of degrees of freedom is about 107 (or more). By introducing a mixed formulation of magnetostatic problems with corrected electric currents, we have proposed an iterative domain decomposition method for magnetostatic problems based on the mixed formulation, and then we have simplified the systems by using properties of the Lagrange multiplier. The product of matrices and vectors appearing in the procedure comes down to a magnetostatic problem in each subdomain, therefore the method is applicable to parallel computing, where the large systems can be solved effectively. The convergence properties of an iterative procedure are improved, and the cost of computations can be reduced. Therefore, we have computed larger numerical models, which has not been solved before. By applying such an effective approximation method, we can perform numerical simulations to understanding of the phenomena of magnetic fields and to optimal design of transformers.
Finally, we extend our interests to the understanding of other phenomena, for example, viscoelastic flows, moving boundary flows, and interference and scattering of light, and so on. Then, numerical simulations could be performed by mathematically justified methods.

Arithmetic invariant theory and related geometry

ISHITSUKA, Yasuhiro
Degree: PhD (Science) (Kyoto University)
Research interests: Number theory, Arithmetic invariant theory, Diophantine geometry
My main research interest is a subject called arithmetic invariant theory. It belongs to number theory, a branch of algebra. The objects and methods are described as follows (see Figure 1):
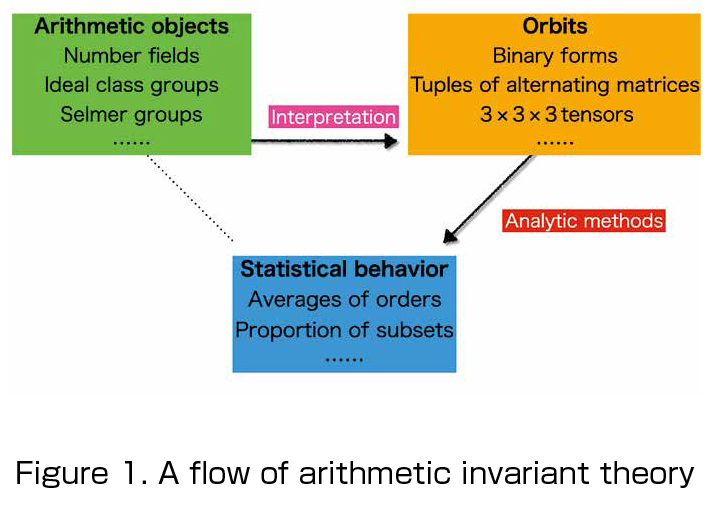
(1) Objects: The subject studies arithmetic objects which are interested in number theory; for example, algebraic number fields and its ideal class groups, Mordell—Weil groups of elliptic curves over rational number fields. Number fields and elliptic curves are easily constructed, but to compute their class groups or Mordell—Weil groups is often a difficult task. Moreover, it drastically change when we change its parameters. We then consider their statistical behavior such as the “average” order of ideal class groups, or the “proportion” of elliptic curves with high Mordell—Weil rank.
(2) Methods: We interpret arithmetic objects as orbits of linear representations of algebraic groups. This sometimes enables us to replace the counting problem of arithmetic objects to the counting problems of lattice points in a fundamental domain. In such cases, we can apply techniques of analytic number theory, and discuss the average or proportion of arithmetic objects.
Along this scheme, I treat the proportion of plane cubic curves admitting a linear determinantal representation (for example, Figure 2).

Actually, we also study the plane cubics whose Jacobian variety has a positive Mordell—Weil rank.
I am also interested in explicit construction of curves with arithmetic properties, and study properties of explicitly given curves. An example is a construction of plane quartic curves which fails the local—global properties of the existence of bitangents. Bitangents of a plane quartic curve is a line in plane which tangents to the curve at two points, or tangents quadruply at one point (Figure 3). A smooth plane quartic over the rational number field does not need to have a bitangent defined over the field. In a joint work with T. Ito et al., we explicitly construct a smooth plane quartic which admits a bitangent locally, but not globally. Besides arithmetic geometry, we use computer algebra systems.
In both topics, we study classical topics of algebraic geometry and invariant theory in arithmetic settings. It gives a new perspective of objects; for example, the correspondences between arithmetic objects and orbits used in arithmetic invariant theory are valid over the complex number field, but difficult to find detailed structures since it is very simple. I am particularly interested in those structures appearing over arithmetic settings.
Modeling of Solid-to-Solid Phase-Transformations in Shape-Memory Alloys Homogenization and Gamma-Convergence Problems for Nematic Elastomers
CESANA, Pierluigi
Degree: PhD (Applied Mathematics)(SISSA International School for Advanced Studies, Italy)
Research interests: Partial Differential Equations, Variational Problems
The main focus of my research work is on rigorous mathematical modeling and analysis of multiscale and multiphysics systems in materials science. My investigations explore ways information and disorder emerge and evolve generating complexity and patterns in smart materials such as martensite, nematic elastomers and liquid crystals. Understanding the microscale features and mechanisms of multifunctional materials and predicting their interactions on the overall macroscopic properties is of strategic importance in the design of materials for engineering applications. Two specific lines from my past and current research are summarized below.
1) Solid-to-solid phase-transformations in shape-memory alloys
Austenite-to-Martensite phase transformation is observed in various metals, ceramics and biological systems. It is the activation mechanism of the Shape-Memory effect. Despite the vast potential to the shapememory effect, practical implementations have been slow, and to-date, mostly limited to NiTi. It is strategically important to improve and stabilize the shape-memory effect in known materials and develop new modeling strategies. A problem I have considered is the analysis and modeling of disclinations (topological defects at the lattice level characterized by rotational mismatch). Disclinations as in Fig. 1-a are characterized by a self-similar triple-star pattern resulting in intense rotational stretches. Mathematically, I have shown that such configurations arise as a solution of differential inclusion problems with special rotational symmetry and rigidity. By identifying the basic algebraic structure underlying the differential inclusion I have computed exact solutions both in linearized and finite elasticity models shedding light on the mechanism that drives formation of triple-stars. Moreover, I have investigated onset of criticality and self-organization in the evolution of martensite via sequential avalanching. Here the modeling strategy describes the nucleation of martensitic variants as a branching random walk process (see Fig. 1-b). The question that I addressed is the behavior of certain features of the self-similar structure thus formed and the computation of power laws for the length interfaces in a martensitic transformation. This project involved collaboration with the groups of J. Ball and B. Hambly (Oxford, stochastic modeling of martensite); E. Vives and A. Planes (Barcelona) and T. Inamura (TiTech) on experiments on avalanches and disclinations in martensite. Work is in progress on the investigation of the activation mechanisms that drive avalanches in metals with the ultimate goal of mechanically characterizing the dynamics of solid-to-solid phasetransformations.
2) Homogenization and Gamma-Convergence problems for nematic elastomers
Nematic Liquid Crystal Elastomers (NLCEs) are a class of soft ShapeMemory Alloys that combine the entropic elasticity of a network of crosslinked polymeric chains with the peculiar optical properties of nematic liquid crystals. A thorough understanding of the manipulation of optical birefringence in thin-films of NLCEs by mechanical, electric and thermal means is a tremendous mathematical task which has strategical potential applications in materials design and fundamental sciences. Focusing on the strain-order coupling in NLCEs, I have investigated mechanisms that rule the low energy states in mechanically and geometrically constrained systems such as artificial muscles, sensors and actuators. The mathematical language required to tackle NLCEs problems is that of calculus of variations, Gamma-convergence and relaxation. These are sophisticated techniques at the intersection of the analysis of PDEs, functional analysis and measure theory based on energy minimization approach and which are particularly suitable for the study of singularly perturbed variational problems. Collaborations are in progress with the experimental Lab of K. Urayama (KyotoTech).
Algebraic specification

GAINA, Daniel
Degree: PhD (Japan Advanced Institute of Science and Technology)
Research interests: Universal Logic, Formal Methods, Category Theory
Universal logic is a general study of logical structures with no commitment to any particular logical system in the same way that universal algebra is a general study of algebraic structures. The term “universal” refers to the collection of global concepts that allow one to unify the treatment of the logical systems and avoid repetition of similar results. One major approach to universal logic, in terms of both number of research contributions and significance of the results, is institution theory. This relies upon a category-based definition of the informal notion of logical system, called institution, which includes both syntax and semantics as well as the satisfaction relation between them. As opposed to the bottom-up methodology of conventional logic tradition, the institution theory approach is top-down: the concepts describe the features that a logic may have and they are defined at the most appropriate level of abstraction; the hypothesis are kept as general as possible and they are introduced only on by-need basis. This has the advantage of proving uniformly results for a multitude of logical systems. It leads to a deeper understanding of the logic ideas since the irrelevant details of particular logics are removed and the results are structurally obtained by clean causality. My research interests cover, roughly, institution theory and its applications to computing science.
(1) Foundation of system specification and verification
There are many contributions of institution theory to computing science, the most visible one is providing mathematical foundations for the formal methods techniques, i.e. specification, development and verification of systems. In algebraic specification, one of the most important classes of formal methods, it is a standard and mandatory practice to have an institution to underlie each language basic feature and construct; institution theory sets a standard style for developing an algebraic specification language that initially requires to define a logical system formalized as an institution and then develop all the language constructs as mathematical entities in the framework provided by the underlying institution.

(2) Reconfigurable software systems
The main direction of my research consists of developing logical structures supporting the efficient development of correct reconfigurable software systems, i.e. systems with reconfigurable mechanisms managing the dynamic evolution of their configurations in response to external stimuli or internal performance measures. A typical example of reconfigurable system is given by the cloud-based applications that flexibly react to client demands by allocating, for example, new server units to meet higher rates of service requests. The model implemented over the cloud is pay-per-usage, which means that the users will pay only for using the services. Therefore, the cloud service providers have to maintain a certain level of quality of service to keep up the reputation. Generally speaking, reconfigurable systems are safety- and securitycritical systems with strong qualitative requirements, and consequently, formal verification is needed.

(3) System development
I am currently maintaining the Constructor-based Theorem Prover (CITP), a proof management tool built on top of an algebraic specification language for verifying safety properties of transition systems. The methodology supported by the tool is not intended for formalizing mathematics, but for the application to the development of software systems. In order to achieve the targeted goal, the following important research directions are pursued:
(a) proposing more expressive logical systems to allow engineers to specify easily and accurately the software systems,
(b) develop decision procedures that can reason efficiently about these more sophisticated logics, and
(c) improvements of the proof assistant interface to help the user understand the current state of the proof and interact with the tool in a more natural way.
The interest is in the design of software systems as one can see in the table below.
The system will be specified at the most appropriate level of abstraction depending on the requirements for its behavior. The result of the verification performed with the tool will determine if improvements of the design are required or not.