私は、低次元トポロジーとよばれる純粋数学の一分野を研究しています。より詳しくは、4次元の図形を曲面の上に“描く”理論があり、この4次元と2次元が相互に影響し合う関係に強い魅力を感じ、研究しています。

　4次元を描く方法の説明の前に、次元を落とした簡単なモデルを見てみましょう。次の図のように細長い長方形の紐を用意して、両端を張り合わせることを考えます。張り合わせ方は二通りあり、一方からは普通の輪っか（アニュラスといいます）ができ、もう一方からは捩じった輪っか（いわゆるメビウスの帯）ができます。このとき図のように、アニュラス、メビウスの帯の下に仮想的な円周をそれぞれ置くと、円周の各点の上に短い線分が並んだような構造があることが見てとれます。円（1次元）の上に線分（1次元）が並んで、全体としては１＋１＝2次元の図形となっているわけです。

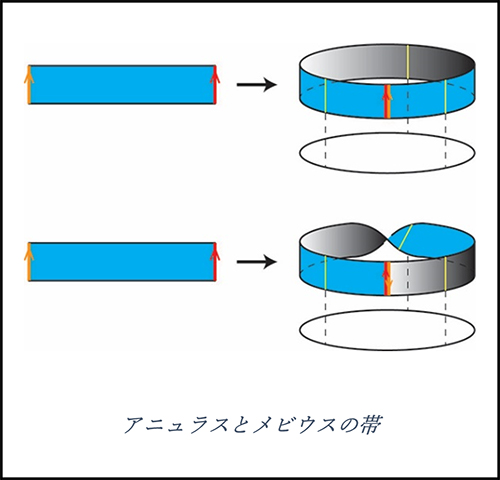
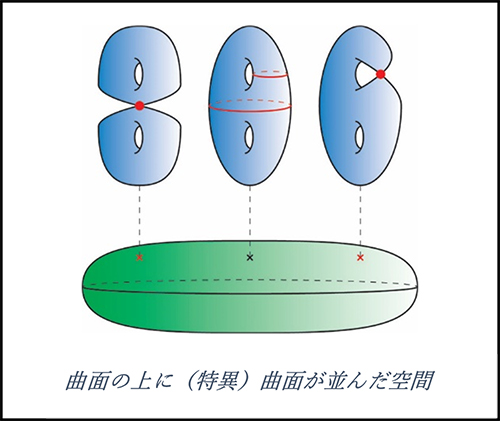
　想像力を膨らませてこの考え方を発展させると、曲面（2次元）の上に曲面（2次元）が並んだ空間というものが考えられ、この空間の次元は２＋２＝４次元になります。さらにもう少し条件を緩くして、次の図のようにときどき特異点をもった曲面があらわれることも許すことにすると、非常に豊かなクラスの4次元図形（専門用語でシンプレクティック4次元多様体といいます）を扱えるようになります。
　上に並んでいる曲面をファイバーといいますが、ファイバーの上に特異点に対応する閉曲線を描けば、考えている4次元多様体の情報をすべてもった「設計図」が得られます。もう少し正確には、この設計図はファイバーの曲面に付随する写像類群という群の言葉で記述されるものです。

　こうして4次元多様体と曲面の写像類群が関係づき、4次元多様体の制約から写像類群の性質が得られたり、逆に写像類群の議論から4次元多様体の性質が得られたりと相互補完的な研究があります。
　私がもっとも得意とするのは、上で説明した写像類群における「設計図」を作ることです。これまでに、基礎的な例をみつけたり、再利用が可能な使い勝手の良い設計図を作ったり、またそれらをもとに複雑な設計図を作ることで存在が知られていなかった4次元多様体を構成したりしてきました。

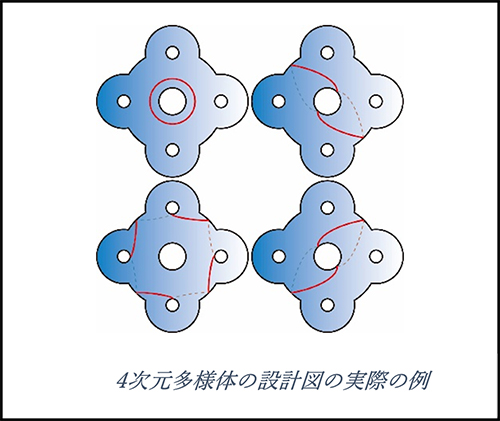
　ところで4次元多様体の分類の仕方として、2つの多様体が“連続的に”移り合うとき同じとみなす同相の立場と、“滑らかに”移り合うとき同じとみなす微分同相の立場があります。この2通りの区別の違いは非常に繊細であり、4次元トポロジーでは中心的な話題です。近年の私の（共同）研究では、ある標準的な4次元多様体に同相であるが微分同相ではない4次元多様体というものを多く発見しており、4次元における同相と微分同相のギャップについての新たな知見を得ています。