双曲型偏微分方程式は解の有限伝播性やホイヘンスの原理等重要な数学的特徴を持つ。数理科学の分野での重要性はもちろんのこと、力学や波動をはじめとする様々な自然現象のモデル化が可能であるため、これまで物理学や工学の分野においても重要な役割を担ってきた。中でも、存在する解の情報から支配される方程式系を決定する逆問題は、数理科学の分野では非適切性問題として極めて重要である。加えて物理現象の背景を詳細に理解できるツールとしても強く注目されている。

偏微分方程式の逆問題における代表的な研究課題は、未知の波源を特定する波源項決定逆問題と、方程式が記述する未知の物理的性質を特定する係数決定逆問題である。考えている領域の一部で波動を観測した観測者が、これらの未知量を観測領域の近く或いは考えている領域全体で特定できるかどうかを調べることが目的となる （図１）。

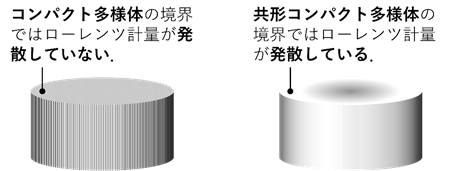
様々な偏微分方程式のタイプがある中で、特に双曲型偏微分方程式は座標に依存しない幾何学的な記述が可能である場合が多い。したがって例えば不定値な計量を導入した擬リーマン多様体上における解析との相性が非常に良い。近年では逆問題の様相を幾何学的視点から捉えるべく、コンパクトなローレンツ多様体上の幾何解析を用いた研究が進められている。さらに、物理学からの要請として多様体の境界で計量が発散する共形コンパクトな多様体上での逆問題解析も注目を集めている（図２）。共形コンパクト多様体上では方程式の主要部が退化するため解析が容易ではなく、退化型方程式に対する新たな逆問題理論の構築が必要である。

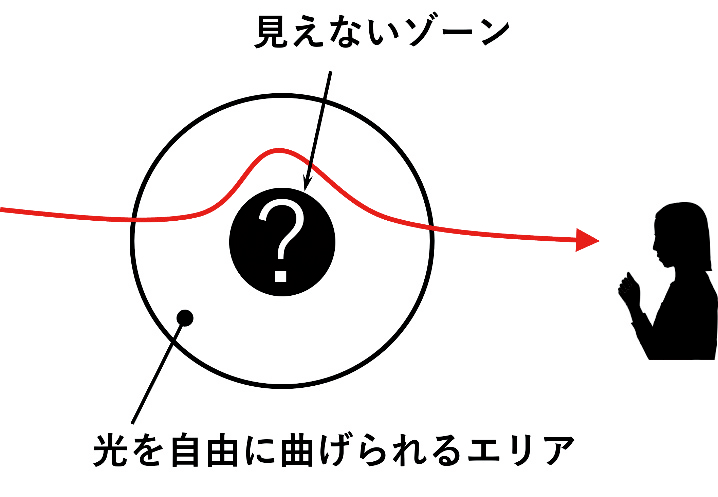
結果の原因となる未知量を特定する逆問題は、当然ながら必ずしも肯定的に解決されるわけではない。否定的な例として、映画「ハリー・ポッター」に出てくる透明マントのような光のクローキング技術がある。これは、ある対象の周りの有界な領域において媒質を変化させることで光の進行を曲げ、外部からの光が伝播しない見えないゾーンを作り出すことでその対象を不可視化する技術である （図３）。偏微分方程式論において媒質の変化はしばしば低階項であるポテンシャルとして定式化される。見えないゾーンにおいてはそのポテンシャルの影響により外部から光が伝播しない状況を、ポテンシャル項付き波動方程式のコーシー問題の観点から理解することもできる。このように否定的な状況を改めて考察することが数学的に面白い構造を発見する上で助けになることもあるのかもしれない。