離散最適化とその応用

神山 直之
学位:博士(工学)(京都大学)
専門分野: 離散最適化,グラフ理論,計算量理論
私の専門分野は離散最適化の理論的研究です.加えて,離散最適化と関係の深いグラフ理論や計算量理論の研究も行っています.これらの分野は数学と計算機科学の落ち合うところに位置し,互いに深く絡み合っています.これらの分野が含む問題は非常に多岐に渡るのですが,私は離散的な凸性である劣モジュラ性や,双対性を基本とする多面体的手法などを通じて,統一的な理解を深めることを目標としています.以下では,私が興味を持っている問題と併せて,これらの分野の簡単な説明をさせていただきます.
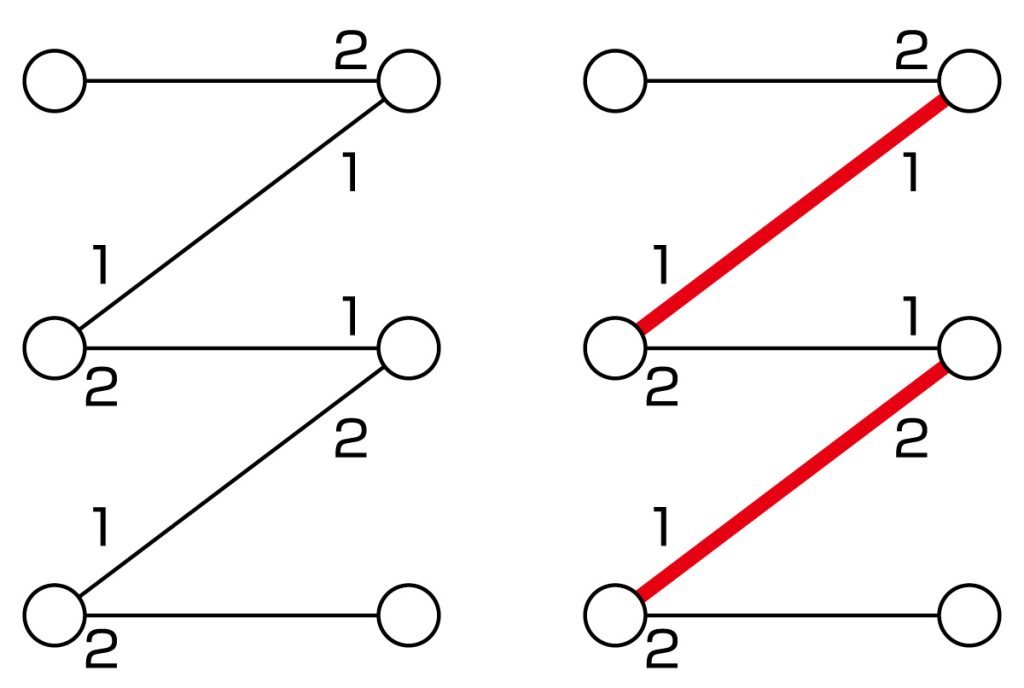
付記されている数字は相手に対する選好順序.(右)割り当ての例.
まず離散最適化ですが,そもそも最適化とは幾つかの解の候補から,目的関数を最大化もしくは最小化する解を求める問題です.離散最適化の研究においては,その中でも解の候補が離散的(つまりばらばら)な性質を持つ問題を扱います.これらの問題に対して,解の集合がどのような性質を満たすならば,全ての解の候補を調べずに効率的に最適解を見つけることができるかを明らかにし,実際にその解を求める方法(アルゴリズムと呼ばれます)を構築することが大きな目標となります.この分野に対して,私は二つの集合間の良い割り当てを求める安定マッチング問題や(図1参照),ものの流れを数理モデル化したネットワークフロー,そして離散最適化における抽象的な枠組みである劣モジュラ関数やマトロイドに関係する最適化問題などの研究を行っています.
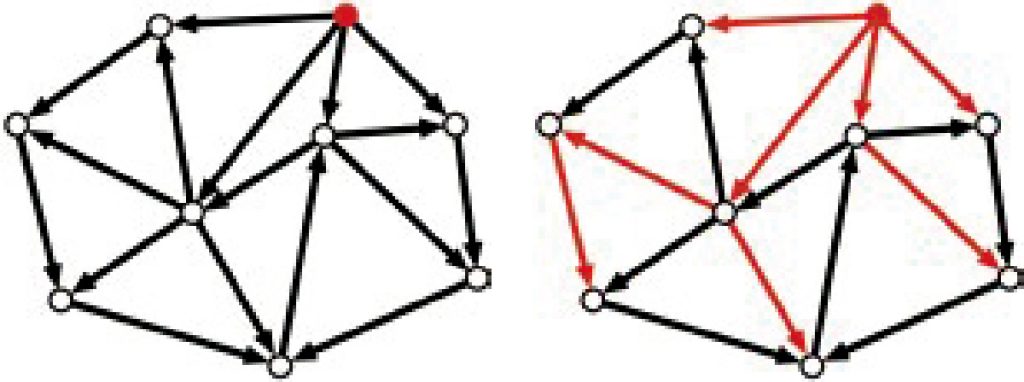
続いては,グラフ理論です.グラフとは点とそれらをつなぐ辺で構成されるもので,幾何学的な位置関係ではなく,位相的にどのように接続しているかのみに注目したものです(図2参照).直観的には,道路等のネットワークを数学的に表わしたものだと思っていただければよいでしょう.そして,グラフ理論とは様々なグラフの持つ特性を一般的に明らかにする学問です.例えば,どのようなグラフならば高い頑健性を持っているかを考えたりします.このグラフ理論においては,私は古典的な問題である有向木の詰込問題における最大最小定理や(図2参照),グラフ上の最適化問題である辺支配集合問題などの研究を行っています.
最後に計算量理論です.上記の二つの分野がどちらかといえば「できる」ことを研究する学問だったのに対し,この分野は「できない」ことを研究する分野です.具体的には,計算機における「計算」を数学的に定義しその能力の限界を研究するものです.この分野においては,クレイ数学研究所の発表したミレニアム懸賞問題の一つである「P対NP問題」が象徴的な問題だといえるでしょう.一見,最適化と計算量理論の分野は相反するものに見えますが,実はそうではなく近年計算量理論の研究においても最適化の手法が使用されるようになってきています.私はこの計算量理論の研究において,離散最適化の分野で用いられている手法,例えば多面体的アプローチ等をどのように活用することができるかを明らかにすることに興味があります.
また,これらの分野の研究は,現実社会の問題を数理モデル化し解決するオペレーションズ・リサーチと呼ばれる分野と非常に相性が非常に良く,私自身も交通や都市計画,そしてソーシャルネットワーク等の現実的な問題から生じる問題に対して得られた理論的成果を応用することに興味があります.

