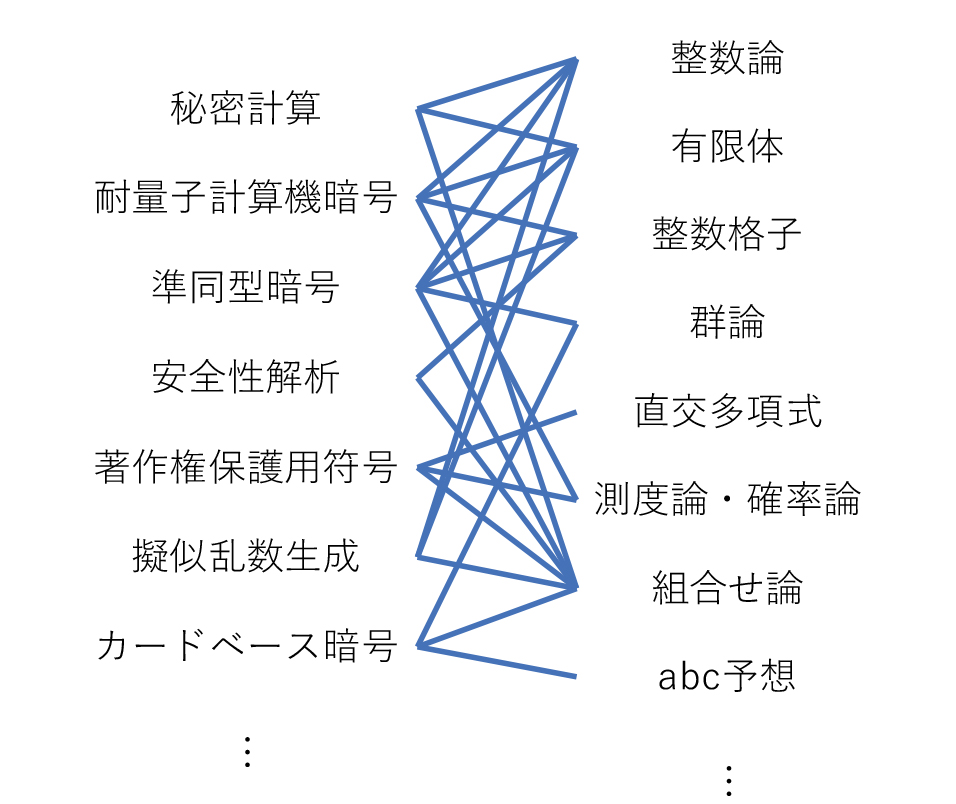
インターネット経由での安全な買い物など，現代の便利な生活の基盤となっている情報技術のさらに基盤となっている技術の一つが暗号技術です．さらにその暗号技術の基盤として数学が役立っています．1970年代後半に考案されたRSA暗号では初等整数論が，1980年代半ばに考案された楕円曲線暗号では名称の通り楕円曲線の性質が活用されています．さらに，来たるべき量子コンピュータ時代に備える次世代暗号（耐量子計算機暗号）には，線型代数やグレブナー基底や高次元整数格子などまた別のさまざまな数学が現れます．

　数学者の目線で暗号分野を眺めたとき，「より新しく多彩な数学を実戦投入する」楽しさはもちろんのこと，それ以外に「素朴な数学的道具でも，使い方次第で大きく花開く」という楽しさや，「安全性」など暗号分野の様々な概念に対して「より直感に沿った，かつ理論的にもより取り扱いやすい「良い」定義を探究する」といった楽しさも感じられます．

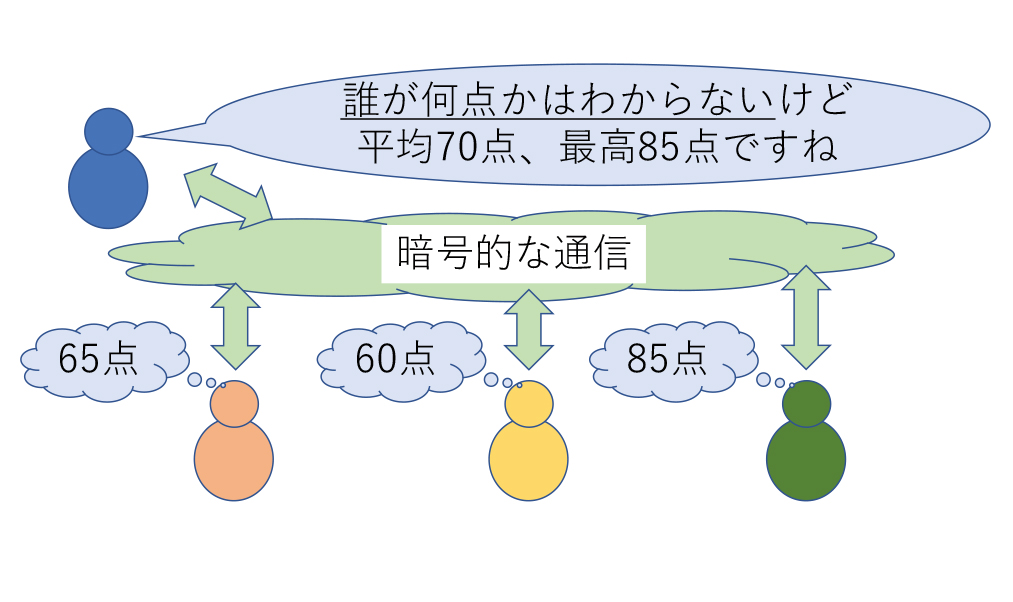
　暗号分野で私が近年主に取り組んでいる研究テーマは「秘密計算」と呼ばれる技術です．秘密計算は，複数人がデータを持ち寄って行う情報処理において，「データを互いに見せない」のに「欲しい計算結果はちゃんと得られる」という手品のような性質を実現する暗号技術です．秘密計算によく用いられる数学的・暗号的な道具のうち，「完全準同型暗号」という技術は，暗号化したままの状態で暗号文の中身のデータに対する計算を行える特殊な暗号化技術です．私たちの論文（国際会議EUROCRYPT 2015で発表）で構成した完全準同型暗号では「有限体上の関数はどれも多項式で表示できる」という性質が要となりました．この性質自体は代数学の初歩的な内容なのですが，それを「上手いタイミングで使う」ことで暗号学的に有意義な成果が得られたという実例となっています．

　この完全準同型暗号については，既存の構成手法においてどうしても外すことのできない複雑な操作が存在し，効率化の妨げとなっています．私の最近の研究では，従来研究で用いられていなかった群論的な手法を用いてこの複雑な操作を回避することを目指しています．この研究には，数学における私の専門である組合せ論的群論の知見も活用できると見込んでおり，その意味でもやりがいのある研究です．

　他にも秘密計算に関する最近の研究として，従来この分野で安全と考えられてきた「直感的にもっともらしいある種の構成法」が実は安全でない場合があることを示す「病的な反例」を発見しています（国際会議PKC 2021で発表）．これもある意味で「いかにも数学者的」な研究でしょう．

　これらの事例に限らず，暗号分野には（他の応用分野でもそうでしょうが）本当に多種多様な数学が関わっていて，私自身の研究でも「まさかこんな数学が役に立つとは」と驚いたことが何度もありました．そうした数学と暗号との豊かな関連性についての情報発信もより一層進めていきたいと思っています．