生物は長く過酷な生存競争を生き延びてきただけあって，生命現象の内には巧みで洗練された技術が多くあります．私の研究ではこのような生命現象を数式で書き表すことによって生命の持つ技術を理解・抽出し，工学・工業的な応用へと繋げる事を目標としています．

鉄道網や蟻の列，血管網に葉脈など，輸送に関する様々なネットワークがあります．これらは全て使われている経路が発達し，使われて無い経路は縮退していく性質があります．このようなものを適応ネットワークと呼びます．これらの適応ネットワークの形状は状況に応じて最終的な形状が（毛細血管や大動脈のように）大きく異なります．このような適応ネットワークの形成を理解することが本テーマの目的です．

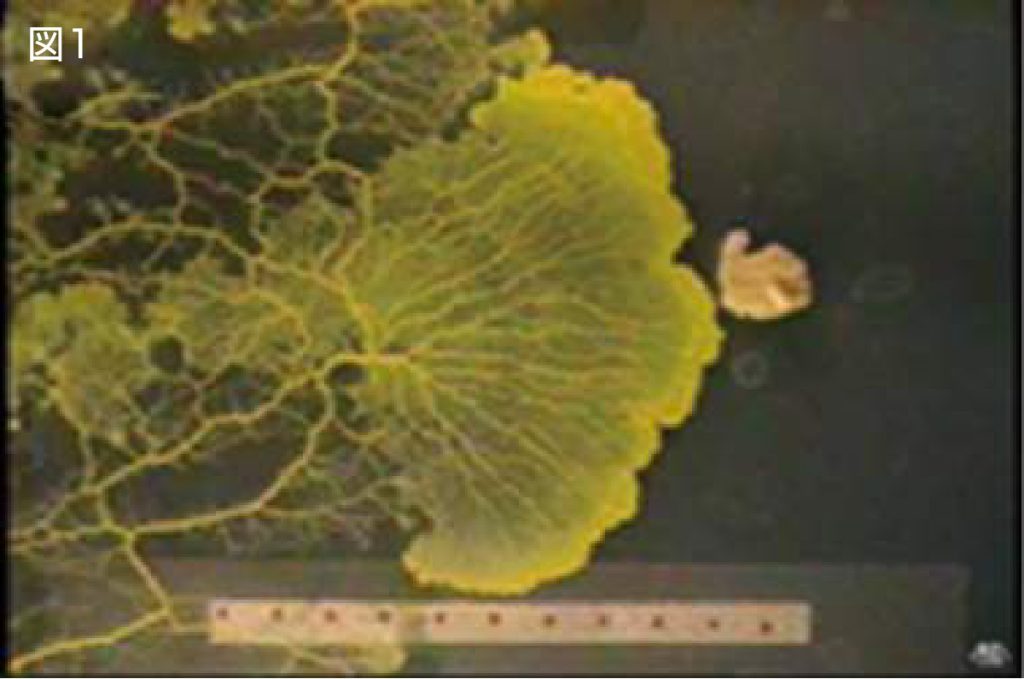
私がこの研究に用いた生物は真正粘菌変形体という生き物です（図１）．粘菌は単細胞生物ですが，体内に栄養等を輸送する適応ネットワークを持っています．また，内部に核をたくさん持った集団的な性質も持った生き物です．例えばナイフで幾つかに切断すればそのそれぞれが別個体として生存できるし，反対にくっつけてしまえば１つの個体として生活することができます．粘菌はこのように切ったり貼ったりが自由にできることから適応ネットワークを理解するのに優れた素材になっています．この粘菌が作る輸送ネットワークは迷路を解き，最適なネットワークを求めるという実験が共同研究者の中垣俊之教授（はこだて未来大学）により行われました（図２a-c）．しかし脳が無く自分の周りの情報しか持たない粘菌がどのようにして大域的な情報が必要なネットワーク問題を解くことができたのでしょうか．

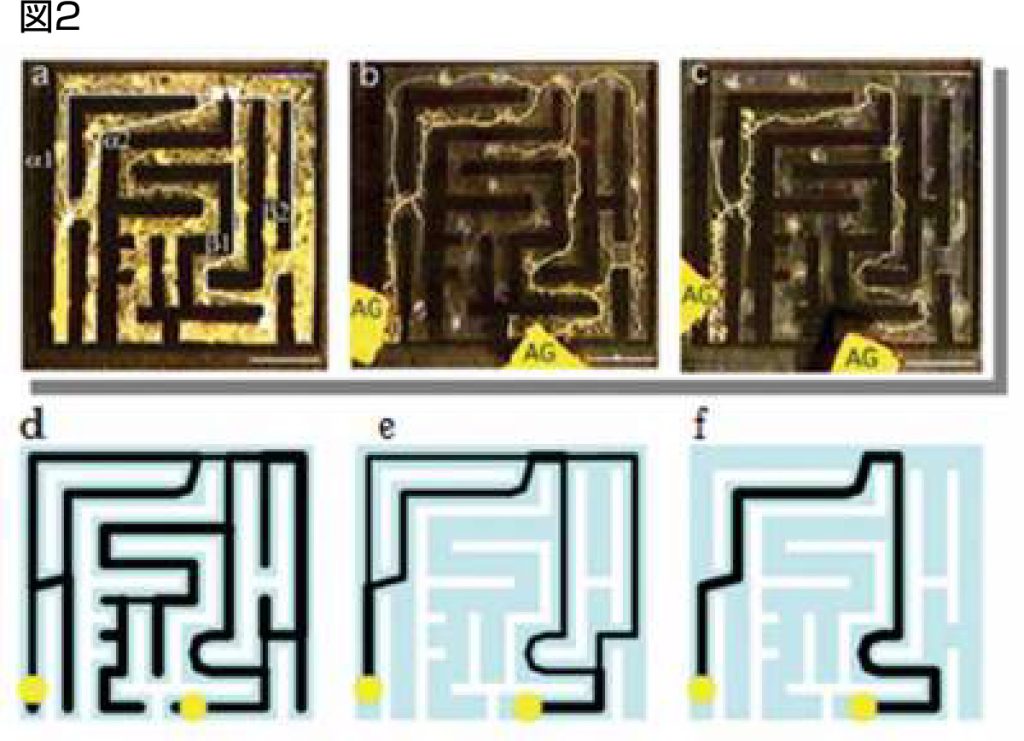
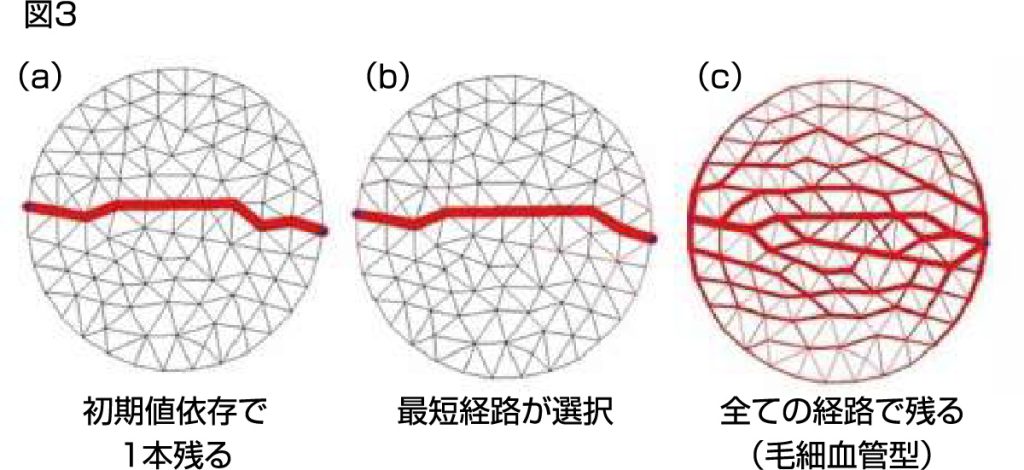
私はこの現象を数式で表すことによりこの現象を再現しました（図２d-f）．その結果，この最短経路解が求まるパラメータを境界にしてネットワークの形が大きく変わることがわかりました．適応ネットワークの成長率が太い経路ほど強かった場合，図３aにあるように経路は１本だけ残ります．これは初期状態で太い管が成長しやすく，その後，より一層成長しやすくなっていくからである．反対に太い経路ほど維持コストが高ければ太い管は細い管に血流を奪われてしまい，全ての経路が残ります(図３c)．このように粘菌が迷路を解くという研究の私の数理モデルはこの２つのネットワーク形成の境界を与えているのです．このためネットワークトポロジーが変化する場合には必ず図３bの状況を通過するので，適応ネットワークの組み換えを知るには図３(a-c)のパラメータに注目すれば良いのです．

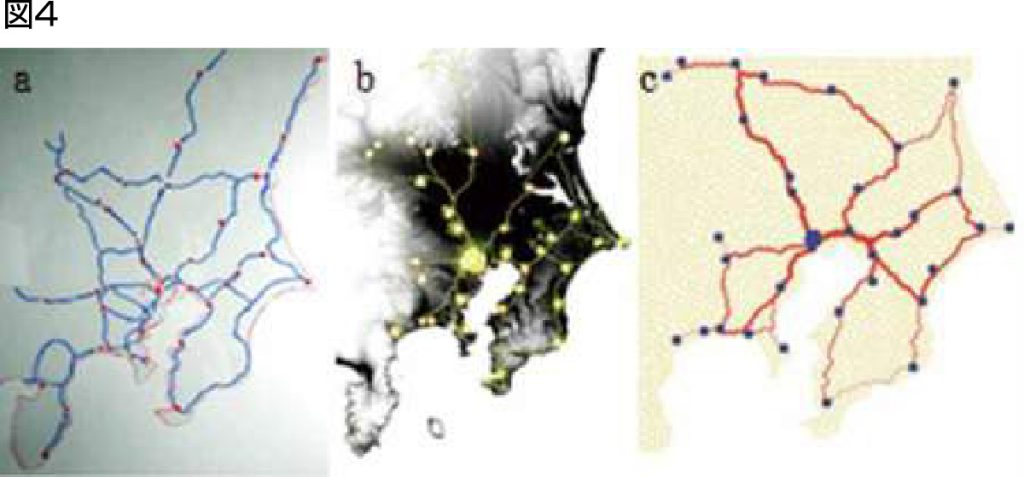
このようにして適応ネットワークの共通法則が得られたため，それを一般の鉄道網に応用しました（図４a-c）．これからはさまざまな適応ネットワークに対してこの共通法則を応用し，工学・実用的な結果へと繋げていくことを目標とします．

また，他にも生物の多様なリズムを用いた行動制御や生物の自発的な形態形成についての研究も行っております．