近年，ビッグデータ解析が重要視されていますが，データ量が多くなった反面，データの冗長性も増してしまい，必要のない情報を取り除いて有効な情報のみをうまく抽出することが必要とされています．それを実現する，極めて有効な方法の一つが，L１正則化法をはじめとする，スパース推定です．スパース推定とは，数万・数億にものぼる数のパラメータが存在するときに，ほとんどを「ゼロ」と推定することができる方法であり，非ゼロ要素に対応する変数のみが有効となります．この方法の良い所は，たとえ数万オーダーの次元のデータであっても，わずか数分で計算が完了してしまうくらいに高速なところです．計算効率が良い上に，統計的にも良い性質がたくさんあるため，L１正則化は多くの統計学者を魅了しているのではないかと思います．

私は，上記のL１正則化法を使った統計解析，とくに，多変量解析に興味を持っています．多変量解析とは，大量の変数があった時，似た変数をうまくまとめたりすることにより，変数間の関係性を見出す方法です．この方法は，古くから現在までずっと使われ続けている基本的な手法です．私は，多変量解析の中でも，因子分析と呼ばれる手法に興味を持っています．因子分析は，もともと心理学者が作った方法なのですが，近年は生命科学でも使われています．また，因子分析を拡張したテンソル分解は，機械学習の分野で使われ始めています．因子モデルの研究は今後ますます発展していくと考えられます．以下，私の最近行った２つの研究を紹介します．

（１） 因子分析のスパース推定

因子分析の面白い点は，モデルそのものに識別性がないというところです．このような解が一意に存在しないモデルは，統計学者からすると「奇異なモデル」となります．実際にどのようにパラメータを推定するかというと，因子回転と呼ばれる，因子分析独自の最適化問題を解きます．このような問題設定自体，他のモデルにはない独特なものですが，それが50年以上も使われてきたスタンダーダードな方法です．

私は，この因子分析モデルにL１正則化を適用すると何が起こるかを考えてみました．すると，正則化法が，因子回転の一般化であり，更に因子回転よりもスパースな解が得られるということを理論的に示すことができました．私はこの関係性を見出しただけでなく，パラメータをある程度高速に推定できるアルゴリズムを考え，さらにソフトウェアパッケージfanc（https://cran.r-project.org/web/packages/fanc/index.html）を作りました．実際にこのパッケージを使った論文もいくつかあります．

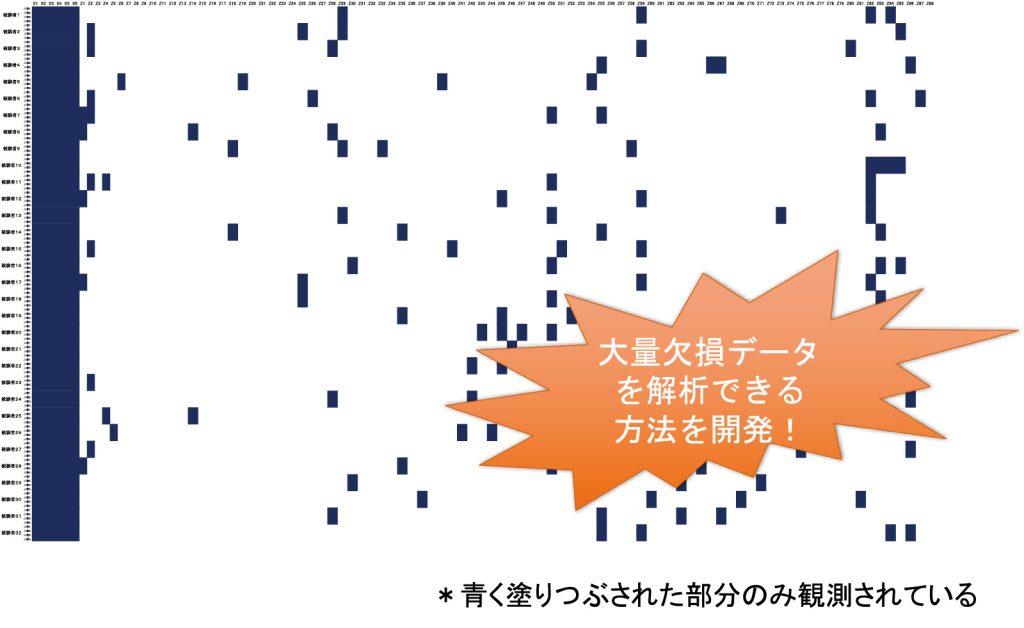
（２） データが大量に欠損する場合の因子分析モデルの最尤推定

NTTと共同研究している際，データに大量の欠損がある場合の因子分析をしなければならないということがありました（図参照）．具体的には，アンケートを行う際，すべてのアンケート項目に答えるのでなく，その中のごく一部を選び，その選んだ項目のみ回答するというデータの取り方をしました．

データが欠損する場合，パラメータはEMアルゴリズムによって推定できますが，欠損数が多い場合，通常のEMアルゴリズムだと計算時間がかかってしまいます．そこで私は，大量欠損時の因子分析モデルにおけるEMアルゴリズムを提案しました．このアルゴリズムは，従来のEMアルゴリズムよりも，数百倍，場合によっては数千倍もスピードが早い事がわかりました．