「変な振る舞い」=「素直な振る舞い」

松江 要
学位:博士(理学)(京都大学)
専門分野: 力学系、数値解析、精度保証付き数値計算、特異摂動論、燃焼など
物体の動き、空気の流れ、物体や空間の温度など、多くの自然現象は微分方程式の解で記述されます。典型的に、解は徐々に(定数や時間周期的な振動する関数などで記述される)一定の状態に近づく、あるいは指数関数的に発散しますが、時折この枠組みに当てはまらない「特異」な動きをするものがあります。例えば u’ = u2 (’は時間微分)について、時刻t=0におけるuの値を正の値に取ると、解はある有限の値Tに対して、t→Tの時に無限大に発散し、それ以降方程式は「解けなく」なります。
これは典型的な物理現象では起こり得ない「変」な振る舞いで、解が「有限時間爆発」すると言います。有限時間爆発は熱源着火に付随する熱暴走、連鎖的化学反応による反応暴走、エネルギー集中に伴う極短時間における梁の急激・爆発的な振動など、特異な現象の数学的対象物としてしばしば確認されます。一方、上の方程式が示すように「系=現象の支配法則」自体は特異性がない場合も多く、与えられた系に対して「爆発は起こるのか」、起こるとすれば「いつ、どこで、どのように」起こるのかは非自明な問いであり、このような振る舞いを制御するには現象そのものの理解を深める必要があります。他方、爆発現象の場合は「無限大」あるいは「無限遠」を直接相手にするため、数学的にも数値的にも捉えることが難しく、この現象そのものが長年の数学的な研究対象とされています(図1参照)。
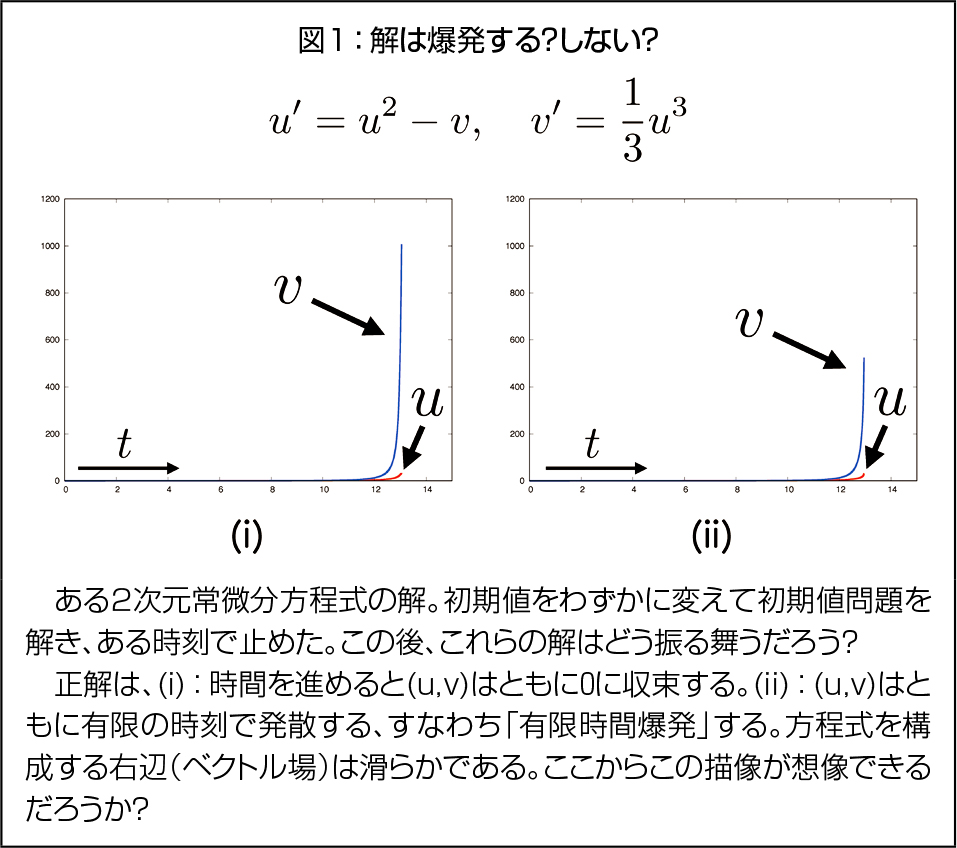
ここで私は、「無限遠」など変・特異な振る舞いを誘発する因子の捉え方を変えることで、物体の動きや温度と同じように「素直」に爆発現象などの「変な振る舞い」を捉え、統一的記述を実現することを研究テーマの1つとしています。具体的な1つのアイデアは「空間全体を半球面やカットされた放物面の中に埋め込み、その境界として無限遠を表現する」というものです。複素関数論におけるリーマン球面、位相空間論におけるコンパクト化に類するものですが、ここでは系の持つスケール性にも着目し、適切な(境界つき)曲面への全空間の埋め込みを構成し、その境界:「地平線」として無限遠を表現します。この考え方自体は代数幾何学などで見られる特異点や無限遠点の捉え方に端を発するものですが、全ての解のとり得る(定性的な)振る舞いを包括的に記述する力学系理論と組み合わせることで、「無限大に発散する解=地平線上の集合に収束する解」という対応を得られます。さらに、地平線への収束の仕方から、変換する前の解の爆発の様子を正確に記述することも可能になります。これは力学系理論の幾何学的側面、代数幾何学由来の系の適切な変換、漸近解析を組み合わせて実現されるものです。
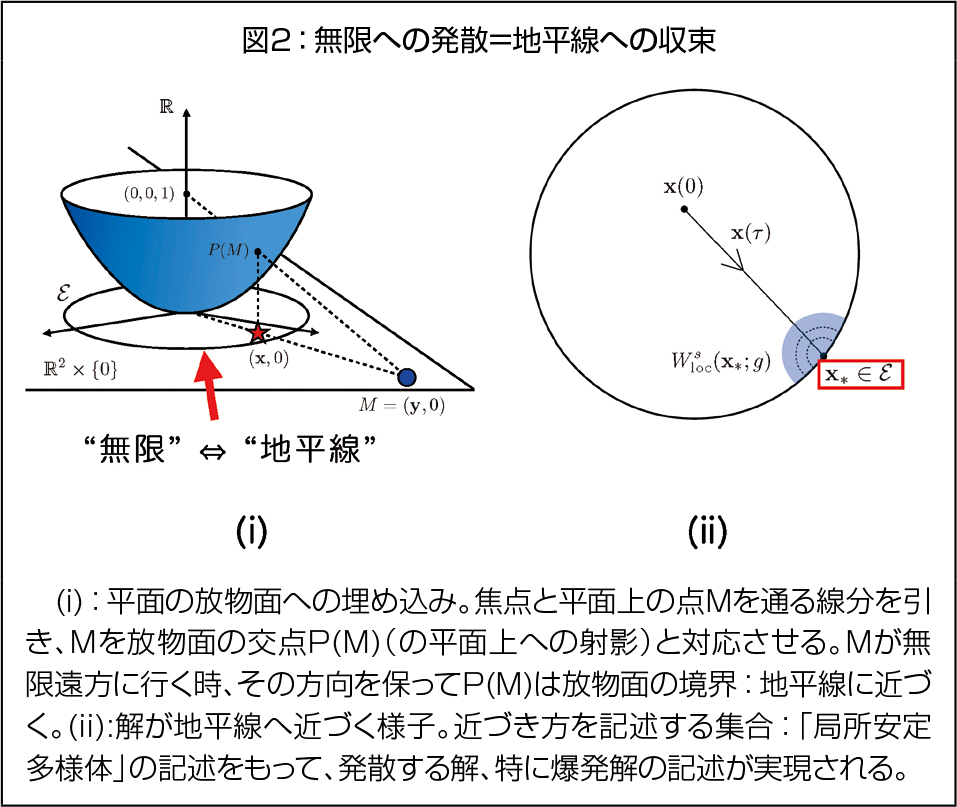
このアプローチの利点の1つとして、数値計算・数値解析など、他の理論や技術との親和性が非常に高いことが挙げられます。(1):爆発の有無を含めた解の振る舞いを網羅する、(2):初期値の摂動で壊れてしまう爆発解を、数学的厳密性をもって数値計算する、(3):「複雑」な爆発の様子も地平線の様子で正確にわかる、などです。これらは精度保証付き数値計算、特異点論などを組み合わせることで実現できます。
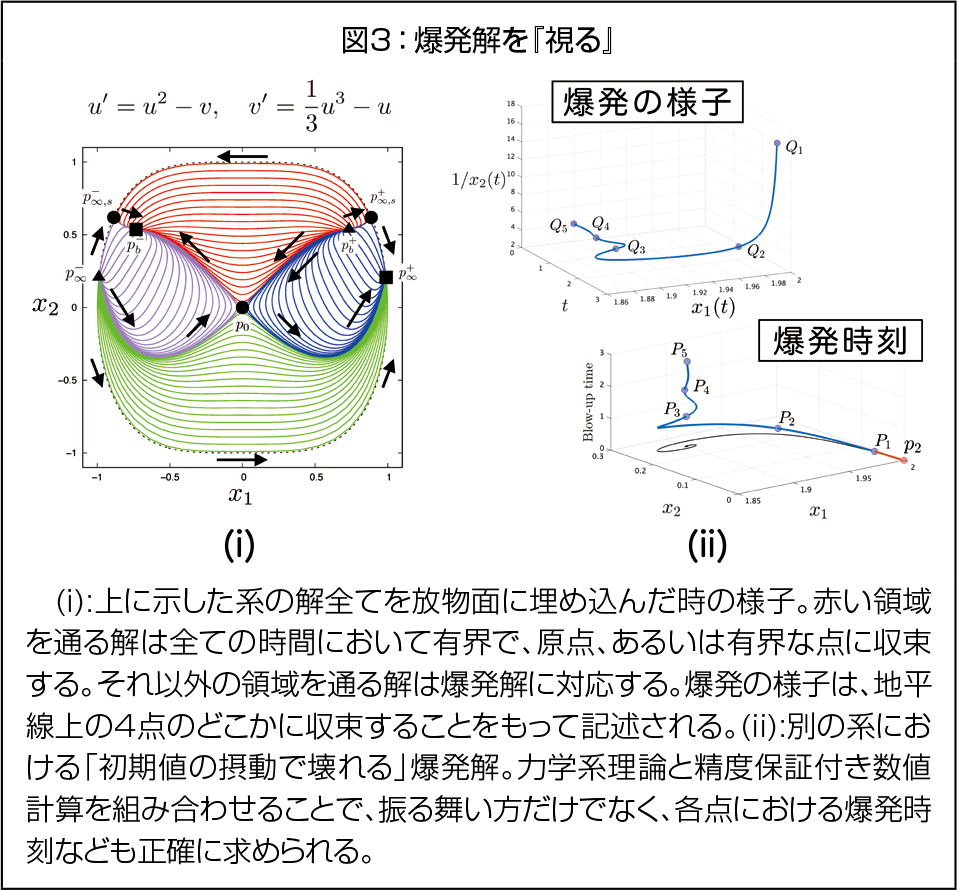
解の爆発だけでなく、時間に付随して起こる様々な変な振る舞い:「有限時間特異性」は捉え所が難しいものです。しかし、上記のように見方を変えることで、実は別な角度から見た素直な振る舞いに過ぎないことが徐々に明らかになっています。この考え方は、古くはマルチスケールダイナミクス、最近では転換点(Tipping point)なども、力学系理論や幾何学の知識で「素直な解釈」が可能となっています。これらを包括的に記述する思想は、様々な点で「変なもの」=「素直なもの」という見方を得ることに繋がるでしょう。

