テータ函数で非自明な的を狙う

重富 尚太
学位:博士(機能数理学)(九州大学)
専門分野: 可積分系、離散微分幾何学、応用物理学、テータ函数
楕円テータ函数というよい性質を持った特殊関数を一つの軸として(1)可積分系とそれに関連する幾何学、(2)応用物理学の研究をしています。楕円テータ函数は数多くの恒等式を満たすことや、擬二重周期を持つことで知られており、数学の幅広い分野に登場します。私の研究の場合、こういった性質は、可積分系の厳密解を構成することに活用できます。また逆に、解の情報から方程式を離散化したり、非自明な保存量を発見したりするときにも重要となってきます。以下、テータ函数の応用例について、具体例を交えつつ紹介します。
(1)可積分系とそれに関連する幾何学
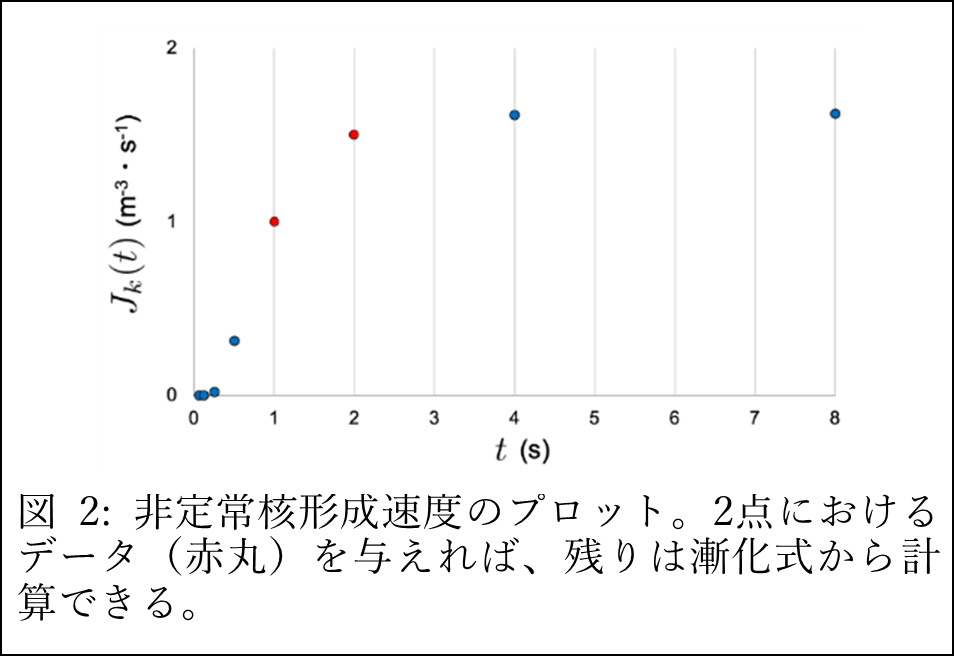
可積分系とは、非線形であるのにも関わらず、よく知られた函数で厳密解が構成できてしまう微分方程式の族のことを指します。また、解の性質を保つ離散化が可能であることも可積分系の著しい特徴の一つです。可積分系の応用例は様々なものがありますが、その中でも離散的な曲線や曲面の研究は、CGや建築、リンク機構などの産業的実用性が高い分野で活用できるという点で重要です。例として、メビウスカライドサイクルを挙げます。これは、6つ以上の合同な四面体を蝶番で環状に繋げて作るリンク機構で、変形の自由度が1であること、複数の保存量を持つことなどから、数学・物理学・工学的に大変興味深い機構ですが、通常、リンク機構の厳密な解析は容易ではありません。ところが、この機構を捩率一定の離散曲線として捉えれば(図1)、その変形が可積分系で記述されることが分かり、曲線の捩率や曲率のみならず、位置ベクトルまでもがテータ函数で明示的に構成できてしまいます。この結果により、これまで知られていなかった保存量などが発見されており、今後のカライドサイクルの解析で重要な役割を担うものと考えられます。
(2)応用物理学
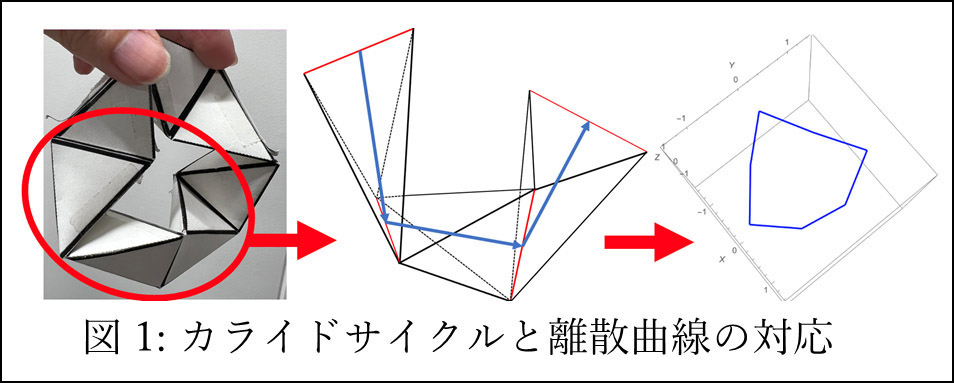
テータ函数は物理学の研究にも登場しますが、私の研究では、地球科学などに見られる応用物理学的な現象の解析にテータ函数の活用を進めています。例えば、核形成と呼ばれる現象は、発泡や結晶化に代表される物理現象であり、極めて身近に観察されるものです。定常過程に至るまでの再初期段階を非定常核形成と呼び、この現象を特徴づける量が非定常核形成速度 Jk( t ) です。この量の測定には、長時間にわたる実験が必要な場合があり、コストの面で課題があります。一方で、 Jk( t ) は楕円テータ函数の特殊値で表されることが1969年に指摘されていましたが、発表以来一度もテータ函数の性質を活用した研究はありませんでした。今回、テータ函数の恒等式を駆使することで、Jk( 2nt ) が満たす非自明な漸化式を導出し、少ないデータで Jk( t ) の値が推定できるようになりました(図2)。これによって、非定常核形成の実験研究におけるコスト削減が期待できます。