私は放物型偏微分方程式を中心に研究しています。ここでいう「放物型」ですが、これは偏微分方程式の分類の1つで、最も基本的な放物型偏微分方程式として熱方程式が挙げられます。

　例えばフライパンをコンロで加熱した際、フライパンの温度の推移は熱方程式に従います。もちろん実世界の現象は多様な外的要因に依存しますのでそれほど単純ではありませんが、理想的な状況下では物理現象を微分方程式によって表現できます。この熱方程式は最も基本的な例ですが、他にも様々な物理現象を放物型偏微分方程式によって表現できます。例えば(水などの)非圧縮性粘性流体の運動方程式であるNavier–Stokes方程式系や、細胞が特定の化学物質に反応して凝集する現象(走化性現象)を表すKeller–Segel方程式系などです。

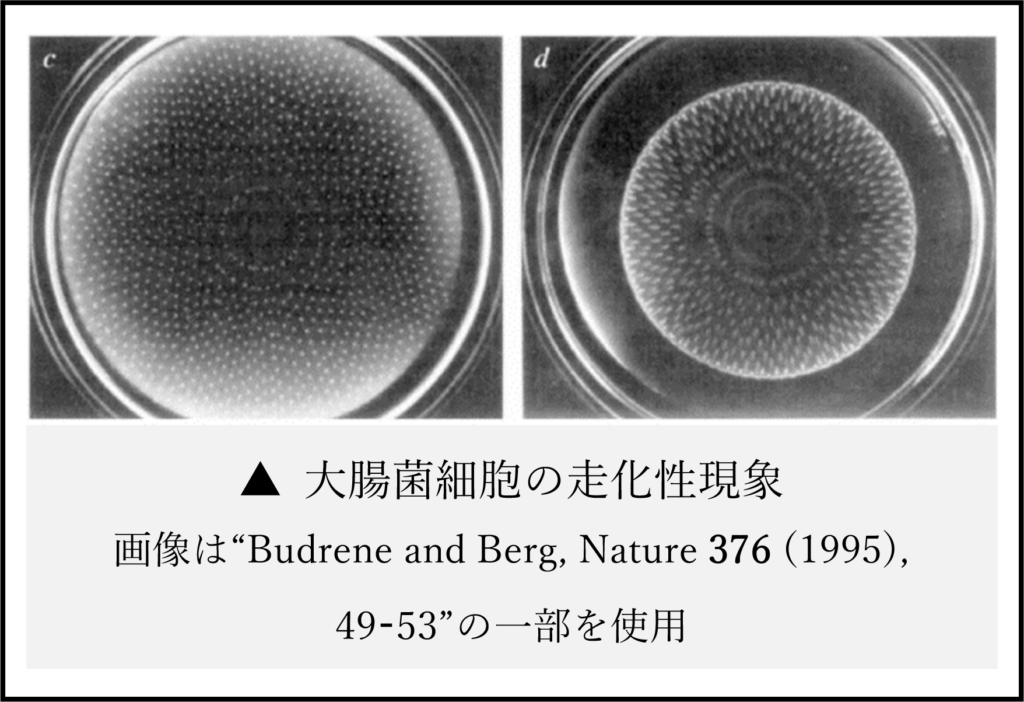
　なおNavier–Stokes方程式系は流体力学の基礎であり、気象学や機械工学をはじめとした多くの実社会への応用分野を支えています。一方Keller–Segel方程式系はがん細胞の転移現象やアルツハイマー病の進行現象に応用され、こちらも医療技術において重要な位置付けにあります。このように、(放物型)偏微分方程式の数学解析は、種々の物理現象を解明して実社会へ役立てる基礎的な役割を果たしています。
　それでは実際に放物型偏微分方程式をどのように解析するか考えてみましょう。微分方程式論における最も基本的な問いは、「解が存在するかどうか」です。微分方程式によって物理現象が表されていれば、理論的な解析はせずとも数値シミュレーションで現象を予測できます。しかし、本当にその微分方程式が物理現象を正しく表しているかは定かではなく、微分方程式に数学的な解が存在しない可能性があります。もしそうならば、存在しない解を数値シミュレーションで探すことになってしまいます。そのような事情から、まず解が存在することを理論的に裏付けたいということが数学的な動機付けの1つです。特に、私は解の存在が保証される数学的条件の枠組みをできるだけ広げたいという動機があります。
　そこで次に述べたいキーワードが「調和解析」です。微分方程式の解析手法はいくつかありますが、私はその中でも調和解析的手法に基づいた研究を行っています。多くの方がどこかでFourier変換という言葉を聞いたことがあると思いますが、調和解析とはFourier変換を用いた解析のことです。

　微分方程式の数学解析では関数空間の設定が必要不可欠ですが、調和解析に基づいた関数空間の導入は私の研究手法においては非常に強力な道具です。特に、関数の滑らかさを古典的な微分可能性という表現でなく、関数の持つ周波数に応じた増大度で表現できる点が有用で、線形解作用素や特異積分作用素などを容易に取り扱うことができるようになります。
　(放物型)偏微分方程式を調和解析的手法に基づいて解析する研究はこれまでにも多く行われてきました。現在では様々なことが明らかになっている一方で、この方向性の研究にはさらなる発展も期待されています。私の研究もそれらの発展の一助になればよいと考えています。