I am researching a field of pure mathematics called low-dimensional topology. More specifically, there is a theory of “drawing” 4-dimensional figures on surfaces, and I am fascinated by the strong interplay between these 4D world and 2D world.

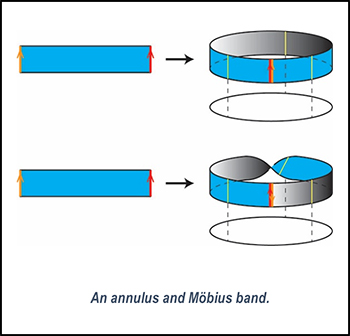
Before delving into the explanation of how to draw 4 dimensions, let’s first look at a simplified model with reduced dimensions. Consider a long rectangular strip and connect both ends, as shown in the following figure. There are two ways to connect them: in one way, a normal loop (called an annulus) is formed, and in the other way, a twisted loop (known as a Möbius strip) is created. Now, we place a hypothetical circle under the annulus and Möbius strip respectively, as shown in the figure, then it can be observed that there is a structure in which a short line segment is arranged above each point on the circle. In essence, lines (1D) are arranged over a circle (1D), resulting in an overall 1+1 = 2D figure.

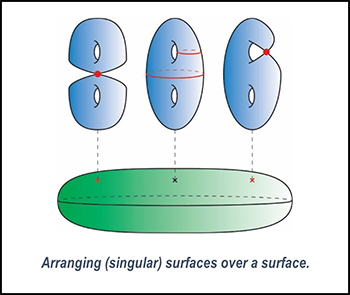
Expanding upon this line of thinking with imagination, one can conceive a space where surfaces (2D) are arranged over another surface (2D). The dimension of this space becomes 2 + 2 = 4D. Furthermore, by relaxing the conditions a bit more and allowing for surfaces above to have occasional singular points, as depicted in the following figure, it becomes possible to handle a very rich class of 4-dimensional objects (referred to in technical terms as symplectic 4-dimensional manifolds).

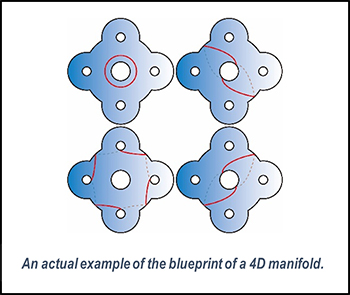
The surfaces arranged above are referred to as fibers. By drawing closed curves corresponding to singular points on a fiber, a “blueprint” that encompasses all the information of the envisioned 4-dimensional manifold can be obtained. More precisely, this blueprint is described in terms of a group called the mapping class group associated with the fiber surface.

In this way, there is a complementary study where 4-dimensional manifolds and the mapping class groups of surfaces are interconnected. For example, from the constraints of 4-dimensional manifolds, properties of mapping class groups have been derived, and conversely, discussions on mapping class groups have yielded properties of 4-dimensional manifolds.

My expertise lies in creating such “blueprints” within the mapping class groups. I have discovered foundational examples, crafted reusable and practical blueprints, and then constructed elaborate blueprints based on them, which established previously unknown 4-dimensional manifolds.

By the way, in the classification of 4-dimensional manifolds, there are two perspectives: the homeomorphic stance, where two manifolds are considered the same when they can be transformed into each other “continuously,” and the diffeomorphic stance, where they are considered the same when they can be transformed into each other “smoothly.” The distinction between these two approaches is highly subtle and is a central topic in 4-dimensional topology. In my recent study with a collaborator, we have discovered many 4-dimensional manifolds that are homeomorphic to certain standard 4-dimensional manifolds but not diffeomorphic. This has provided new insights into the gap between homeomorphism and diffeomorphism in 4D topology.