Bridge between measurements and mathematical modeling via Bayesian inference

Satoru TOKUDA
Degree: PhD (Science) (the University of Tokyo)
Research interests: Research Interests: Bayesian inference, modeling, statistical mechanics
As highlighted by Kepler’s laws of planetary motion since the 17th century, mathematical modeling that describes observed data using simple formulas has deepened our understanding of various physical phenomena. However, observed data are often beyond our understanding in modern science, which makes full use of advanced measurement technologies to capture more complex phenomena. My grand challenge is establishing principles of modeling rooted in observed data to provide guidelines for understanding all phenomena without ambiguity. I am exploring the mathematics of a statistical method called Bayesian inference and promoting empirical research through collaboration with researchers from a wide range of natural sciences focused on condensed matter physics. Through my research to date, I have focused on the following three issues that can make data difficult to understand.
(1) Model uncertainty
Models represent the essence of a phenomenon, but the essence is not always obvious. In many cases, the decision relies on the researcher’s insight, and they sometimes differ in opinion. For example, the vibration phenomenon shown by the observed data in Figure 1 can be modeled by a function that represents simple harmonic motion if friction can be ignored or damped vibration if not, while which is more appropriate depends on the situation.
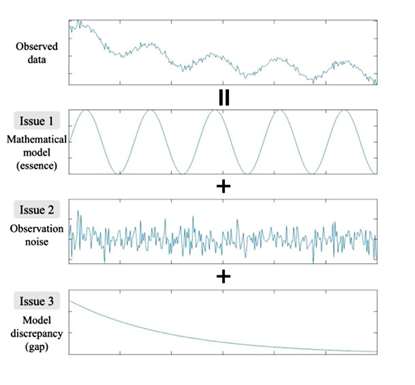
observation noise, and model discrepancy.
We are conducting empirical research to resolve such uncertainties using Bayesian inference, which quantifies the validity of each model against observed data as a probability. We have shown that our approach is useful for selecting models in condensed matter physics, such as velocity distribution functions and band structures.
(2) Observation noise
Measurements involve the observation noise. The parameter values estimated from more noisy data are more uncertain. Focusing on the fact that such an error propagation also affects model evaluation, we have developed a methodology to estimate the noise level and the valid model jointly. We also demonstrated its usefulness through empirical research. Estimating the valid model and its parameter values depends on the noise level (data quality) and data amount. By proceeding with theoretical analysis based on the correspondence between Bayesian inference and statistical mechanics, we have elucidated the scaling law for Bayesian inference depending on the quantity and quality of the observed data.
(3) Model discrepancy
There is always a gap between ideal and reality, that is, between model and observed data. First, a model is an approximate representation of the truth. Additionally, observation noise and systematic errors occur between the truth and the data. Collectively, I refer to everything other than random noise as the model discrepancy. Attributing the origin of model discrepancy is difficult, and it is even more challenging to describe them in concrete formulas. Besides, the traditional asymptotic theory only justifies Bayesian inference by assuming an ideal situation without model discrepancy. Through empirical research, we are developing a methodology to deal with model discrepancy systematically and trying to construct a novel asymptotic theory of Bayesian inference to support its validity.

