Many real-world datasets are heterogeneous and multipopulational phenomena. In such contexts, it is insufficient to capture the overall variation among the data using a single statistical model. Therefore, a cohesive approach to modeling the multiple subpopulations within the superpopulation is necessary. In such scenarios, a useful approach involves modeling each subpopulation and their contributions to the superpopulation through a weighted averaging construction, known as a finite mixture model. These models are highly flexible and interpretable, enabling them to capture and provide inference for known heterogeneities in the data while also identifying new heterogeneous phenomena that were previously concealed.

The class of finite mixture models is extensive, and choosing between different mixture models can be challenging. In my work, I have studied model selection procedures required to make mathematically principled choices among competing finite mixture models. I have made progress in two key directions to address this problem. Firstly, I employ sequences of hypothesis tests to determine the number of components or subpopulations required in each mixture model. This approach relies on a new hypothesis testing method called universal inference, which offers a straightforward and assumption-light mechanism for deciding whether a model accurately represents the observed data. Using these universal inference tests, I have developed a way to construct confidence intervals for the number of underlying subpopulations in the data, providing insight into the complexity of the overall superpopulation.

Secondly, by leveraging modern stochastic programming techniques for optimizing random objects, I have developed new penalization methods for selecting between different finite mixture models within broader model selection and decision problems. My novel information criterion, known as PanIC, offers a more assumption-light alternative to existing methods like the Bayesian information criterion or Akaike information criterion. PanIC provides a single-number summary for choosing between competing models, guaranteed to asymptotically select the correct model as the dataset size increases.

Beyond their utility for modeling heterogeneous processes, finite mixtures and their regression variants, the mixture of experts (MoEs) also serve as excellent functional approximations of probability density functions (PDFs) and conditional PDFs that characterize statistical relationships. My colleagues and I have contributed to understanding the approximation theoretic properties of mixture models and MoEs for various classes of PDFs. We have provided sufficient conditions for ensuring that PDFs, conditional PDFs, or mean functions of conditional PDFs can be effectively approximated using a sufficiently large number of components in a finite mixture model construction. These results, often referred to as universal approximation theorems, are valuable for determining whether a class of functions serves as an adequate basis for modeling an underlying mathematical phenomenon.

My research in mixture model computation, estimation, and inference has found widespread application in real-world scenarios. For example, I have collaborated with neuroscientists and cell biologists to analyze heterogeneous biological phenomena, worked with quantum physicists to characterize switching behaviors of quantum circuitry, assisted economists in characterizing subpopulations of experimental outcomes, partnered with civil engineers to study regional differences in traffic behavior, supported fisheries scientists in characterizing growth stages of aquatic species, and collaborated with image scientists to segment and characterize imaging data, among other practical applications.

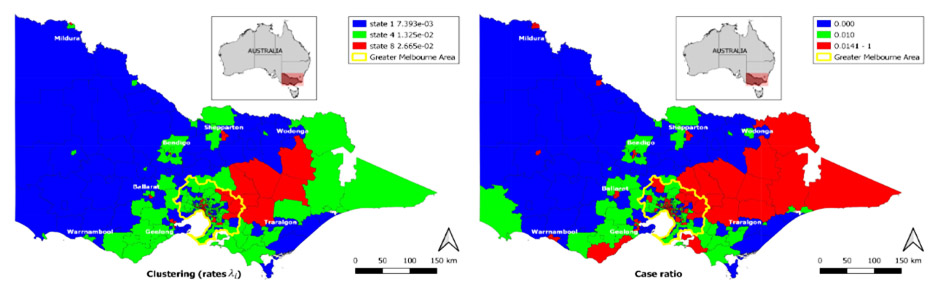
Figure 1: Traffic crash rate clustering of different regions in Victoria, Australia.

Figure 2: Quantization of mandrill photograph using different mixture models.

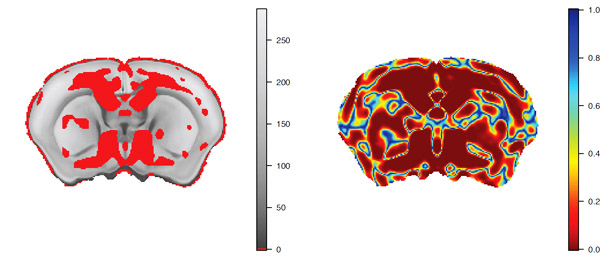
Figure 3: Mixture-based false discovery rate control of p-values for a mouse brain morphometry experiment.