Hyperbolic partial differential equations have important mathematical features such as finite propagation of solutions and Huygens’ principle. In addition to its importance in the mathematical sciences, it has also played an important role in physics and engineering because of its ability to model various natural phenomena such as dynamics and waves. In particular, the inverse problem of determining the governing system of equations from information on existing solutions is extremely important in the mathematical sciences as an ill-posed problem. In addition, it has attracted strong attention as a tool for understanding the background of physical phenomena in detail.

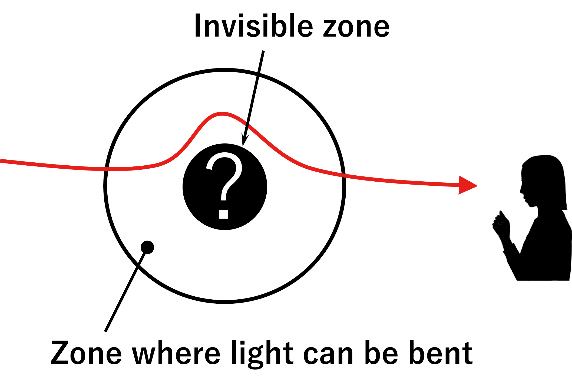
Typical research problems in inverse problems for partial differential equations are the inverse source problem, which identifies an unknown wave source, and the inverse coefficient problem, which identifies an unknown physical property described by the equation. The objective is to determine whether an observer who observes waves in part of the domain of interest can identify these unknowns in the vicinity of the domain of interest or in the entire domain of interest (Fig.1).

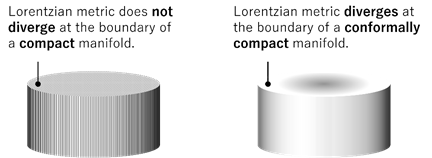
Among the various types of partial differential equations, hyperbolic partial differential equations, in particular, can often be described geometrically independent of local coordinates. Thus, for example, it is very compatible with analysis on pseudo-Riemannian manifolds that introduce indefinite metrics. In recent years, geometric analysis on compact Lorentzian manifolds has been used to study aspects of inverse problems from a geometric viewpoint. Furthermore, as an interest from physics, analysis of inverse problems on conformally compact manifolds where the metric diverges at the boundary of the manifold is also attracting attention (Fig.2). The principal part of the equations on a conformally compact manifold is degenerate, which increases the difficulty, and a new theory of inverse problems for degenerate equations needs to be developed.

The inverse problem of identifying the unknown quantity that is the cause of the result is, of course, not always resolved in the affirmative. A negative example is light cloaking technology, such as the invisibility cloak in the Harry Potter movie. This is a technique to make an object invisible by bending the progress of light by changing the medium in a bounded domain around the object, creating an invisible zone where light from the outside does not propagate (Fig.3). In the theory of partial differential equations, changes in the medium are often formulated as potentials, which are lower-order terms. The situation in which light cannot propagate from the outside in the invisible zone due to its potential can also be understood in terms of the Cauchy problem of the wave equation with a potential term. This renewed consideration of negative situations may help in discovering mathematically interesting structures.