I study combinatorial commutative algebras. One of the fascinating things about intersections of several fields is that we can see things from various perspectives. For example, we have the Pascal’s triangle (see Picture 1). The Pascal’s triangle is defined as follows: In the first row, we put 1. After the second rows, we put 1 to the ends of each row. Otherwise, we put the sum of the left-upper and right-upper. It is well-known that each row of the Pascal’s triangle corresponds to a sequence of binomial coefficients. Moreover, each row of the Pascal’s triangle corresponds to a sequence of the number of faces of some simplex, where the sequence starts the number of (-1)-dimension of the simplex, and the number of (-1)-dimension of the simplex is 1. A simplex is a generalization of points, segments, triangles, tetrahedrons, and so on. Picture 3 is a tetrahedron. You can see that the sequence of the number of faces of the tetrahedron corresponds to the fifth row of the Pascal’s triangle.

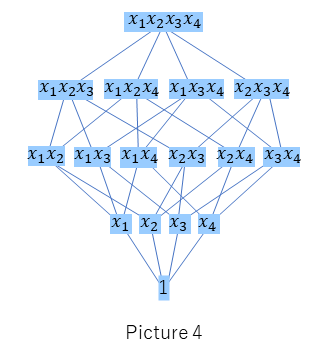
Let us see more deeper about the binomial coefficients. The sequence in Picture 2 is symmetric. We can prove the symmetricity directly. The binomial coefficients are basic conceptions, and they are often appeared in various fields. Now, we prove the symmetricity from the viewpoint of commutative algebras. Let A=k[x₁, x₂, …, x_n]/(x₁², …, x_n²) . Then A is a graded ring which each homogeneous part is a vector space. $(^n_k)$ squarefree monomials of degree k, the products of distinct k variables, is a basis for homogeneous part of k in A. In other words, each dimension of a homogeneous part in A is a binomial coefficient. The bases for A form a poset with the relation of division in monomials as the partial order. Picture 4 is the Hasse diagram in the case of n=4. The algebra A is a Gorenstein, a ring with “symmetricity”. We do not see details in here, but the “symmetricity” of A implies the symmetricity of the sequence of the binomial coefficients. Additionally, we obtain more properties of the sequence of the binomial coefficients from this setup.

We have seen an intersection of commutative algebras and combinatorics using the binomial coefficients as an example, there, however, are many other such examples. There are intersections of various fields, not only commutative ring theory and combinatorics, and the intersections are developing day by day. One of the difficulties to study such areas is that it requires knowledge of various fields. But new discoveries and new perspectives give me pleasure.