In real data, there frequently exist some outliers (observations that are markedly different in value from others) derived from, for example, unusual abilities, catastrophe-level phenomena, or human errors. It is difficult to provide a clear definition or threshold of such outliers, moreover, it is effectively impossible to prevent their occurrence. Thus, robust methods that reduce the influence of outliers have a large significance. My research focuses on robust analytical methods, especially in the model selection problems. I focus on applying statistical divergence, a measure of farness between probability distributions, to examine the closeness of the underlying “true distribution” and models. When selecting a model, the robustness is a desirable property, but most model selection criteria based on the Kullback-Leibler divergence tend to have reduced performance when the data are contaminated by outliers. I have derived and investigated criteria that generalize conventional information criteria such as AIC and BIC, based on the BHHJ divergence, a divergence family that has robustness in parametric estimation.

Since outliers are distant from other observations, they often have a bad influence on values of estimates and model selection criteria. To discuss the robustness of a criterion, we need to evaluate the perturbation of it. In this field, we evaluate the sensitivity of an estimator against contamination, by exploring the difference between populations with and without outlier-generating distribution. We assume that most of observations are drawn from a (true) population distribution, and we can interpret that outliers are drawn from a probability distribution differing from the true distribution (Figure 1). I have investigated the robustness of criteria based on many divergence measures by evaluating the difference of its values between contaminated and non-contaminated data-generating distributions. Consequently, I verified that criteria derived from some class of divergence measures, such as the BHHJ divergence, have robustness in model selection (Figure 2). Since models can be created for all phenomena, it is significant to investigate “good” model selection criteria for all fields. By examining various properties that contribute to selection including robustness, I aim to conduct a research that can support a wide range of fields.

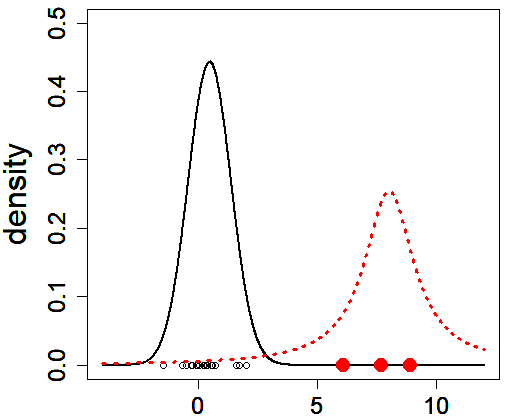
(Caption of Figure 1) We consider two distributions: the “true” population distribution (black curve) and another one that generates outliers (red), and we suppose that observations are drawn from the mixture distribution composed of the two distributions. If a result of analysis varies greatly depending on the presence of absence of outliers, the corresponding method is regarded as to be sensitive against contamination.

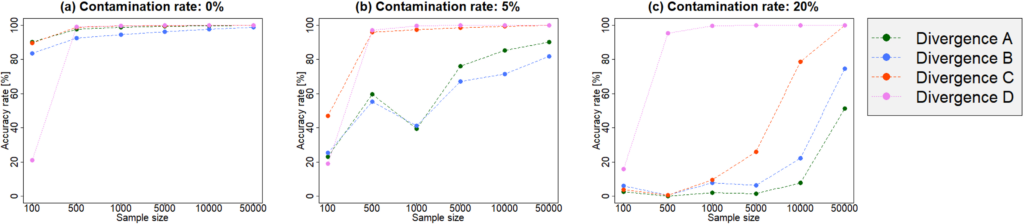
(Caption of Figure 2) Accuracy rates of model selection criteria based on some divergence measures (Divergences A-D) in a numerical simulation of selection problem of the generalized linear model, for different sample sizes and contamination rates. Criteria based on Divergence A and B are sensitive against outliers. In contrast, we can see that Divergence D has strong robustness against contamination of data-generating distribution.