Between the theory of computation and number theory

URAMOTO, Takeo
Degree: Ph.D (Science) (Kyoto University)
Research interests: theoretical computer science
My major interests are broadly in theoretical computer science. In this relation, I’m recently working on intersections between algebraic language theory and classical class field theory.
(1) algebraic language theory
Algebraic language theory is a branch of formal language theory, and historically speaking, has been developed in relation with classifications of hierarchies of languages (= sets of finite words). Intuitively, we feel that it is difficult to judge whether the finite binary sequence, say, 1101110110101 when read as a binary number is a prime number or not, while it is easy to judge whether the number of “0” appearing in 1101110110101 can be divided by 3. In formal language theory (or computational complexity theory), we are interested in classifying the difficulties of such problems on judging some properties of finite words, by formalizing them in terms of some computational models such as Turing machines.
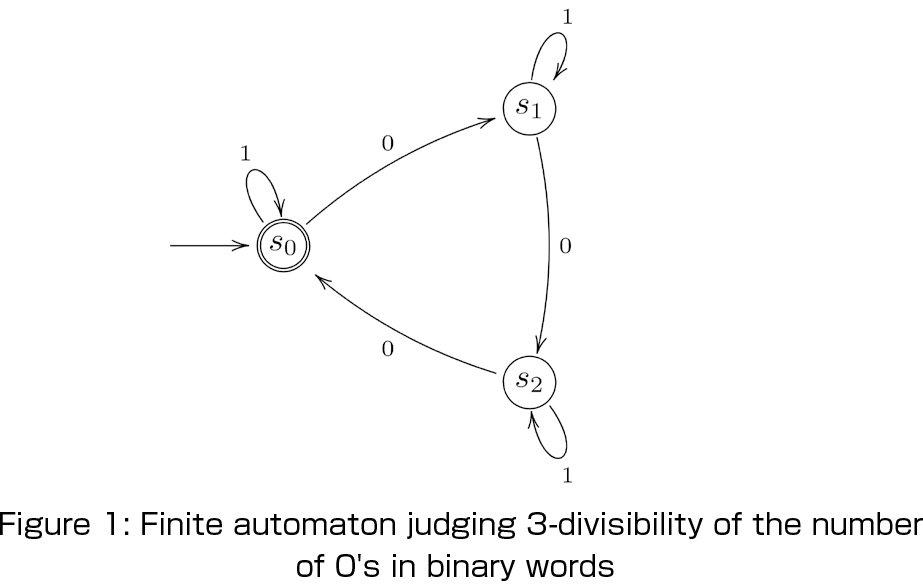
Among several approaches in formal language theory, algebraic language theory is characterized by the use of algebraic methods. In particular, as far as regular languages (i.e. languages that can be accepted by finite automata) are concerned, it is well known that we have a beautiful theory (Eilenberg theory) to classify their hierarchy by means of the theory of finite semigroups. My research also concerns this theory.
Eilenberg theory may be best described by its important instance, Schützenberger’s theorem, which was proved in 1965 in relation with a logical description of regular languages. Before Schützenberger’s theorem, it had been known that regular languages can be characterized as those languages which can be defined by Büchi’s monadic secondorder logic (MSO). In this relation, it had been of concern whether one can effectively characterize when a regular language can be defined by the first-order fragment (FO) of MSO. Schützenberger solved this problem by means of semigroup theory, and this result gave a starting point of Eilenberg theory. After Schützenberger’s work, it has been observed that several hierarchies of regular languages naturally correspond to those of finite monoids, and Eilenberg theory concerns a systematization of such relationship (duality).
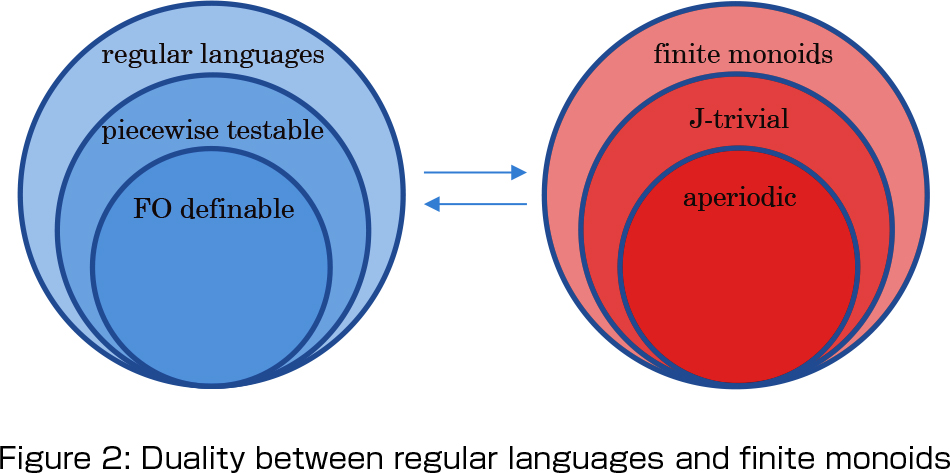
(2) Unification with Galois theory
Technically speaking, Schützenberger’s theorem states that a regular language L is FO definable if and only if the syntactic monoid of L (i.e. a finite monoid canonically attached to L) contains only trivial subgroups. In other words, the FO-definability of regular languages can be characterized by the purely semigroup-theoretic property of the corresponding finite monoids (syntactic monoids M(L)).
This phenomenon is somewhat analogous to the classical result due to Galois: The roots of a polynomial f(z) can be expressed by four arithmetic operations and roots if and only if the galois group of the smallest splitting field K over Q is soluble. In fact, this is not just an “analogy” but can be justified using the abstract language of category theory; and as its consequence, we can unify Eilenberg theory and Galois theory in a certain precise sense. Moreover, it turns out that this unification sheds a new light on classical class field theory, a central field of number theory concerning classification of abelian extensions of number fields. Currently, I’m working on this interesting intersection between classical algebraic language theory (Eilenberg theory) and class field theory, or more specifically, explicit class field theory and nonabelian class field theory.

