My main research interest is a subject called arithmetic invariant theory. It belongs to number theory, a branch of algebra. The objects and methods are described as follows (see Figure 1):

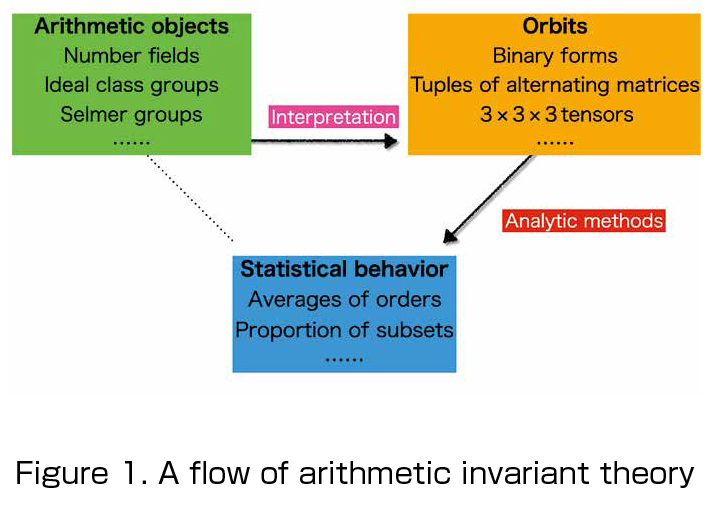
(1) Objects: The subject studies arithmetic objects which are interested in number theory; for example, algebraic number fields and its ideal class groups, Mordell—Weil groups of elliptic curves over rational number fields. Number fields and elliptic curves are easily constructed, but to compute their class groups or Mordell—Weil groups is often a difficult task. Moreover, it drastically change when we change its parameters. We then consider their statistical behavior such as the “average” order of ideal class groups, or the “proportion” of elliptic curves with high Mordell—Weil rank.
(2) Methods: We interpret arithmetic objects as orbits of linear representations of algebraic groups. This sometimes enables us to replace the counting problem of arithmetic objects to the counting problems of lattice points in a fundamental domain. In such cases, we can apply techniques of analytic number theory, and discuss the average or proportion of arithmetic objects.

Along this scheme, I treat the proportion of plane cubic curves admitting a linear determinantal representation (for example, Figure 2).

Actually, we also study the plane cubics whose Jacobian variety has a positive Mordell—Weil rank.

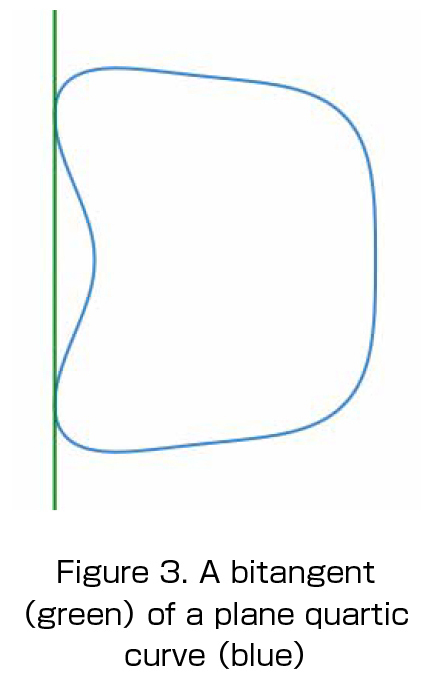
I am also interested in explicit construction of curves with arithmetic properties, and study properties of explicitly given curves. An example is a construction of plane quartic curves which fails the local—global properties of the existence of bitangents. Bitangents of a plane quartic curve is a line in plane which tangents to the curve at two points, or tangents quadruply at one point (Figure 3). A smooth plane quartic over the rational number field does not need to have a bitangent defined over the field. In a joint work with T. Ito et al., we explicitly construct a smooth plane quartic which admits a bitangent locally, but not globally. Besides arithmetic geometry, we use computer algebra systems.

In both topics, we study classical topics of algebraic geometry and invariant theory in arithmetic settings. It gives a new perspective of objects; for example, the correspondences between arithmetic objects and orbits used in arithmetic invariant theory are valid over the complex number field, but difficult to find detailed structures since it is very simple. I am particularly interested in those structures appearing over arithmetic settings.