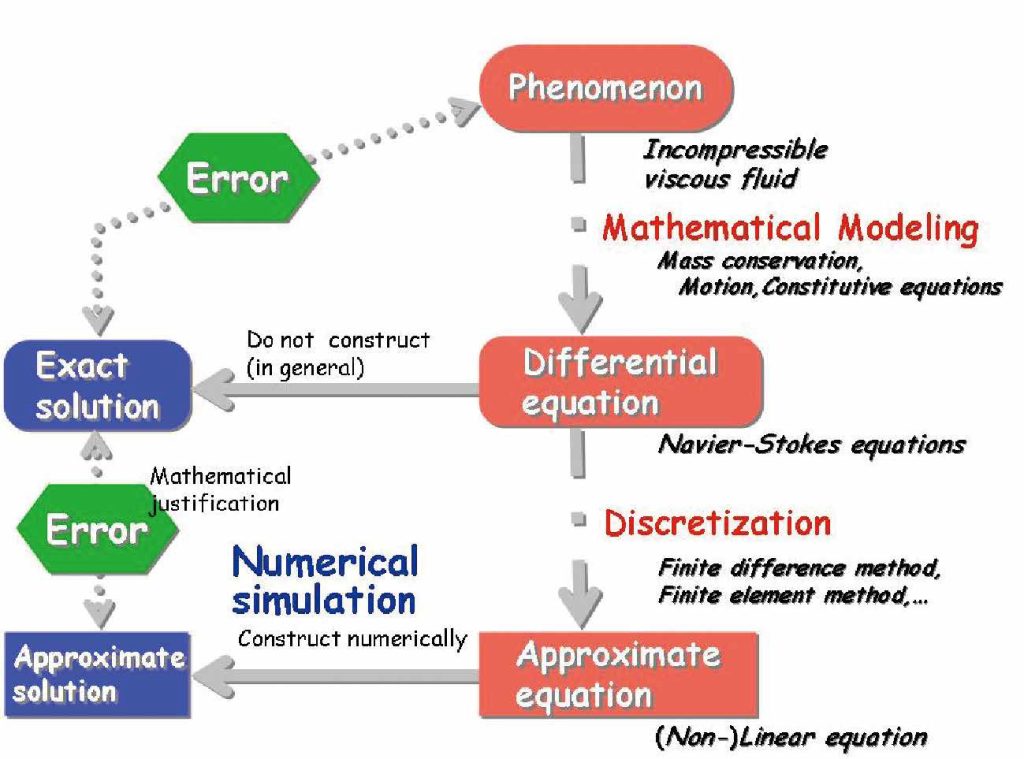
I am interested in understanding phenomena in nature and industry, for example, water flow in rivers and heat transfer in furnaces, by numerical simulations. The numerical simulation consists of three parts: mathematical modeling, discretization, and numerical computation; see Fig.1. First, in the mathematical modeling part, the phenomena are described by differential equations based on physical laws. Next, in the discretization part, the differential equations are approximated by linear systems, which can be handled with computers. Finally, in the numerical computation part, methods to solve the linear systems are implemented in computers to show the phenomena. I focus my attention to proposed numerical simulation methods and to justify the accuracy and efficiency of the methods mathematically. Moreover, I perform numerical computations of various practical problems by using the proposed methods, then I apply them for understanding the phenomena in nature and the design of industrial products.

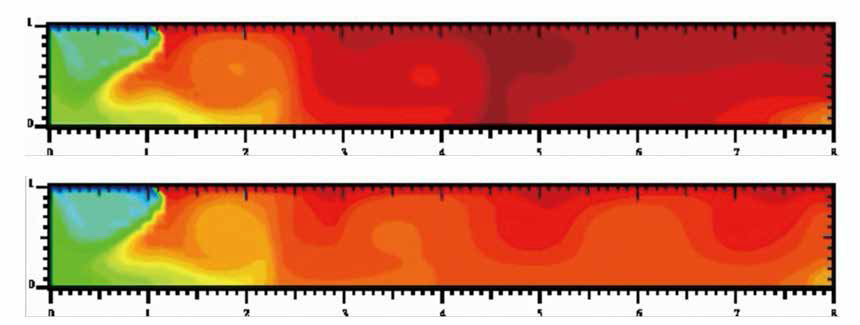
One of my research projects is numerical simulation of the heat transfer phenomenon of glass raw material in melting glass furnaces; see Fig.2. Glass raw material, which is high temperature (about 1,500℃), is considered as an incompressible viscous fluid, so the phenomenon in the furnaces can be described by thermal convection equations with strongly temperature-dependent coefficients. By introducing the backward Euler method in time and the mixed consistent finite element in space, we have proposed numerical simulation methods for thermal convection equations, and have established optimal error estimates of them. Moreover, we have also proposed a numerical simulation methos for heat balance in the whole melting glass furnace, which is based on the consistent flux method. Due to the consistent flux method, we have established optimal error estimates, which imply mathematically that the computation of the boundary flux by the domain integral is more accurate than one by the boundary integral. Therefore numerical simulations based on the mathematically justified methods can be applied to determine the optimal design of melting glass furnaces, which maintains the quality of products and reduces the energy consumption.

Another research project is numerical simulations of magnetic field problems, for example, eddy current problems in transformers; see Fig.3. To obtain accurate numerical simulation results in cases of complicated domains and phenomena, we need to solve linear systems effectively in the numerical computation part , whose number of degrees of freedom is about 10⁷ (or more). By introducing a mixed formulation of magnetostatic problems with corrected electric currents, we have proposed an iterative domain decomposition method for magnetostatic problems based on the mixed formulation, and then we have simplified the systems by using properties of the Lagrange multiplier. The product of matrices and vectors appearing in the procedure comes down to a magnetostatic problem in each subdomain, therefore the method is applicable to parallel computing, where the large systems can be solved effectively. The convergence properties of an iterative procedure are improved, and the cost of computations can be reduced. Therefore, we have computed larger numerical models, which has not been solved before. By applying such an effective approximation method, we can perform numerical simulations to understanding of the phenomena of magnetic fields and to optimal design of transformers.

Finally, we extend our interests to the understanding of other phenomena, for example, viscoelastic flows, moving boundary flows, and interference and scattering of light, and so on. Then, numerical simulations could be performed by mathematically justified methods.