The research for materials structure analysis includes algorithm development based on harmonic analysis, signal processing, optimization and statistics, but I often obtain new findings by combining these with ideas and techniques in pure mathematics including algebra and number theory.
　　The following focuses on my three projects that have resulted in patents.

(1) CONOGRAPH method for ab-initio indexing (lattice determination)

　　”Ab-initio” means an analysis that does not use any prior information on the material structure (in this case the crystal lattice). After publishing papers about fundamental algorithms for the analyses listed below, I released programs for powder diffraction[1] and electron back scattering diffraction[2] far with the support by a lab of KEK I belonged to, and Nippon Steel Corporation.
・ Determination of lattice symmetry (Bravais lattice) under large observation errors　…　Application of lattice-basis reduction theory
・ Peak search
・ Figure of merit for finding solutions that fit experimental data well
・ General rules of forbidden reflections (described using topographs)
・ Method to detect ambiguity (uniqueness of solutions) … Application of arithmetic theory of quadratic forms

　　The software CONOGRAPH enhanced the success ratio in ab-initio indexing. The obtained results can be applied to various lattice-determination problems from diffraction data.

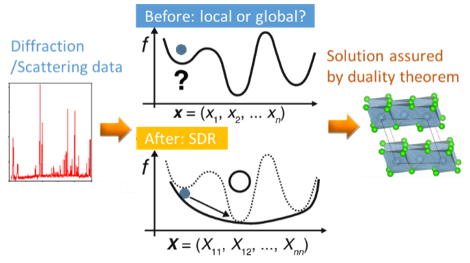
(2) Semidefinite programming relaxation (SDR) to ensure the global optimality

　　Local minimum is a well-known problem in nonlinear optimization. SDR is a method to obtain the global minima of quadratic optimization problems (QP) in a guaranteed situation (Fig.1). In general, phase retrieval to determine the amplitudes of the Fourier transform of the crystal structure (=structure factors) can be expressed as a QP.
　　This study was originally started to investigate the uniqueness of solutions in ab-initio crystal structure determination, but a useful application in magnetic structure analysis was found in a joint work with experimental scientists[3].

(3) Golden angle method for general surfaces and dimensions

　　The generalization of the golden angle method used for modeling phyllotaxis and sunflower heads has been an open problem addressed in various literature. We succeeded in the generalization by attributing it to a problem in geometry of numbers known as “product of linear forms”.

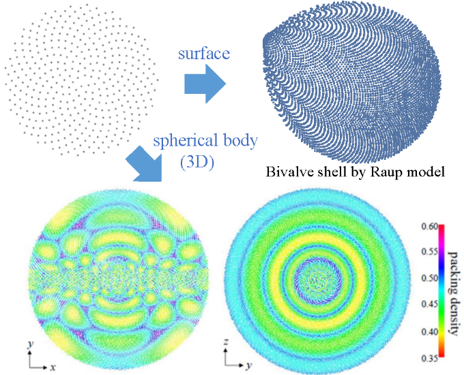
　　We’re now investigating how the developed method and ideas can be applied to modeling, pattern generation and mesh generation.

[1] https://z-code.kek.jp/zrg/
[2] J. Appl. Cryst. (2021) 54 (2), 624-635
[3] Scientific Reports (2018) 8:16228.