Various random phenomena such as lotteries, roulettes, weather forecasts, and stock prices can be seen in everyday life．While such phenomena contain clear randomness, there are some problems to which probabilistic methods can be applied although they do not seem to be random at first glance. I am interested in finding the randomness behind such problems and studying them by using probabilistic techniques.

Here are three examples of such a situation.

(1) Kakutani’s problem, also referred to as the Collatz problem or the 3x+1 problem, is well known. In this problem, we consider a function f on natural numbers such that f(n)=n/2 if n is even and f(n)=3n+1 if n is odd. It is conjectured that repeated iteration of this function eventually produces 1 for every initial value n. For example, if one chooses initially 7, then the sequence becomes 7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1. As of 2009, this conjecture was verified up to 20X2⁵⁸, but it still remains unsolved at present. This problem itself is undoubtedly deterministic (non-random), but, randomness lies behind it.

In the 1960s, a Japanese mathematician Shizuo Kakutani was interested in this problem and circulated it to a number of people. Here I quote his words from a Lagarias’ paper. ”For about a month everybody at Yale worked on it, with no result. A similar phenomenon happened when I mentioned it at the University of Chicago. A joke was made that this problem was part of a conspiracy to slow down mathematical research in the U.S.” (2) The following sequence of letters is a cypher-text that is encoded by a classical method of a simple substitution cypher.

fyeaxj​qfzjoxc​eddedc​jbujcx​bjhxg​pjbeg​xrjukj​zebbe​dcjop​jsxgjz​ezbxg​judjbs​xjofd​ljfdrju​kjsfhe​dcj

Once we realize that this cypher-text is encoded by the method above, we can employ a Markov chain (one of the most basic stochastic processes) to decrypt it. The following is a simulation result of the decryption.

Some coded messages like the above written by a prisoner in the California prison system was brought into a drop-in consulting service in Stanford’s Statistics Department by a psychologist and it was decrypted by Stanford students by using Markov Chain Monte Carlo (MCMC) methods. This is a good example which shows how well MCMC works.

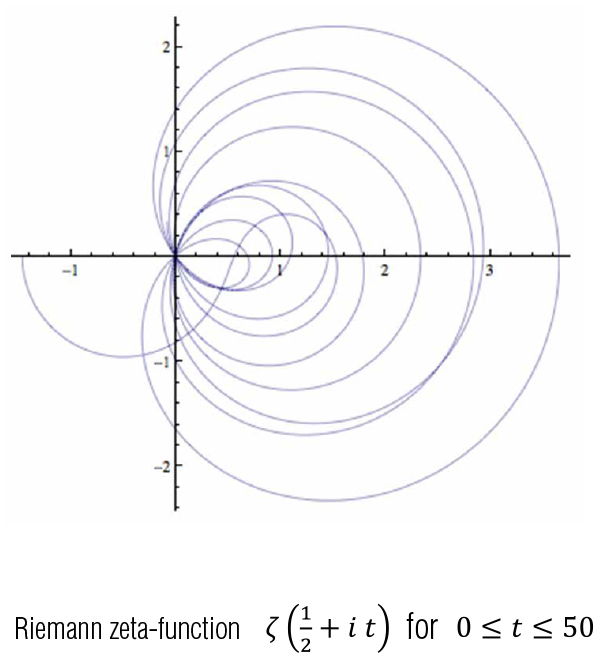
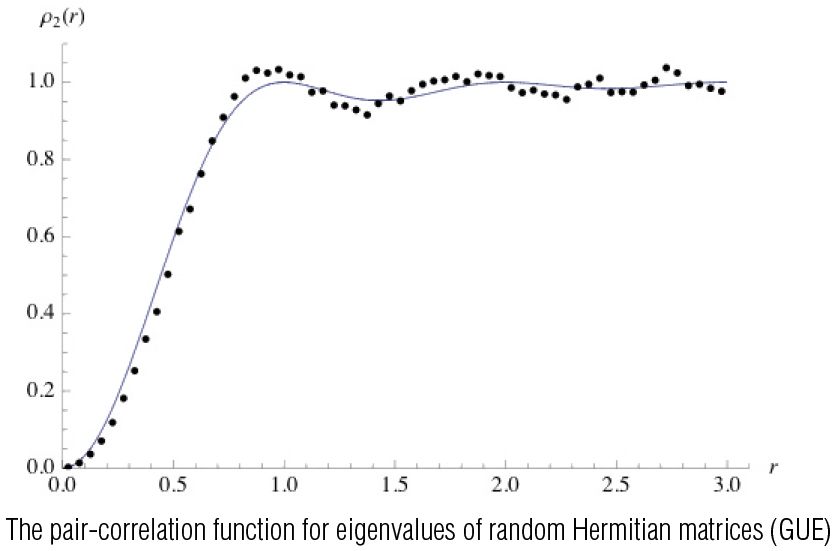
(3) The Millennium Problems are seven problems in mathematics established by the Clay Mathematics Institute in 2000. The Poincare conjecture was solved by Gregory Perelman recently, but, six problems still remain open, among which is the Riemann hypothesis. The Riemann hypothesis asserts that the non-trivial zeros of the Riemann zeta-function defined by $\zeta (s)=\sum ^{\infty }_{n=1}\frac{1}{n^s}$ lie on the so-called critical line Re$(s)=\frac{1}{2}$ The nature of this problem seems to be irrelevant to randomness, but, the zeros are known to look like the eigenvalues of certain random Hermitian matrices.

The mathematician Alfréd Rényi had said that “A mathematician is a device for turning coffee into theorems”. Freeman Dyson, a theoretical physicist, made an interesting comment on a result of Hugh Montgomery, a number theorist, during afternoon tea in the Common Room at the Institute for Advanced Study. This comment shed light on a new aspect of the Riemann zeta-function. This was the very moment that important research was turned in a new direction by a cup of coffee (tea?).

We hope that we can collaborate with one another with an open mind and in an intercultural way at IMI.