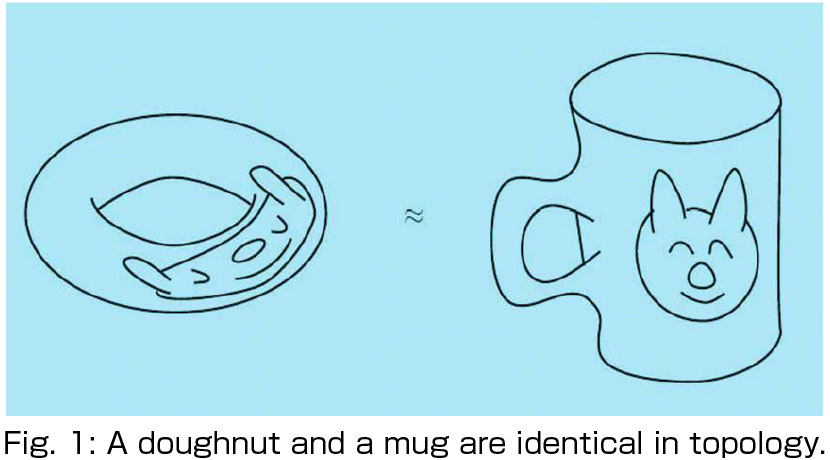
Topology is the study of extremely soft geometry, where an object is regarded as being composed of some soft material, like rubber, and a continuously deformed object is considered to be identical to the original object. In other words, topology is a field of pure mathematics in which we are interested in the properties of geometric objects that do not change as those objects are continuously deformed. For instance, a doughnut and a mug are regarded as identical in topology (see Fig. 1). This is because each of them has exactly one hole, which is a typical example of a quantity that does not change under continuous deformation.

　Given its nature, topology is a powerful tool for analyzing flexible objects. One extreme such example is provided by a string, in which we can create knots and links through various manipulations. These are important actions in daily life and have been part of human existence since a primitive age. In fact, it is known that wild gorillas can tie knots. Moreover, it has recently been found that such knots are deeply connected to research into deoxyribonucleic acid (DNA).

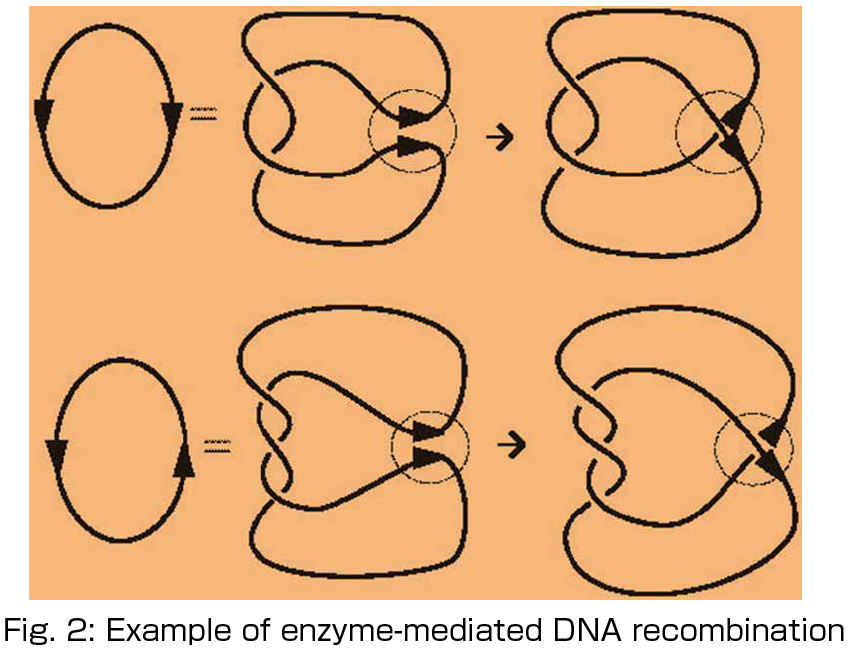
　DNA, taking the form of two twisted thread-like strands, carries hereditary information and exists in the cells of living organisms. This molecule often assumes a ring-like form. Biological observations have shown that strands of ring-shaped DNA are often knotted and linked with each other. Although certain enzymes are responsible for these DNA knots and links (see Fig. 2), due to limitations in experimental techniques the details of the mechanisms involved in such processes have not yet been elucidated. In the late 1980s, the mathematicians C. Ernst and D. W. Sumners used the most recent knot theory in topology at the time to describe some of the mechanisms employed by enzymes. Although it is often said that knot theory has its origin in the electromagnetism of Gauss and the vortex atom hypothesis of Lord Kelvin from the 19th century, chemists and physicists seem to have forgotten about knots, and only mathematicians have maintained this topic as a field of research. Our group is making extensive use of knot theory, which is one of the most actively researched fields in modern mathematics, to analyze DNA recombination mediated by an enzyme called topoisomerase from a mathematical point of view (see Fig. 2). Our main goal is to apply these analyses to industrial technologies.

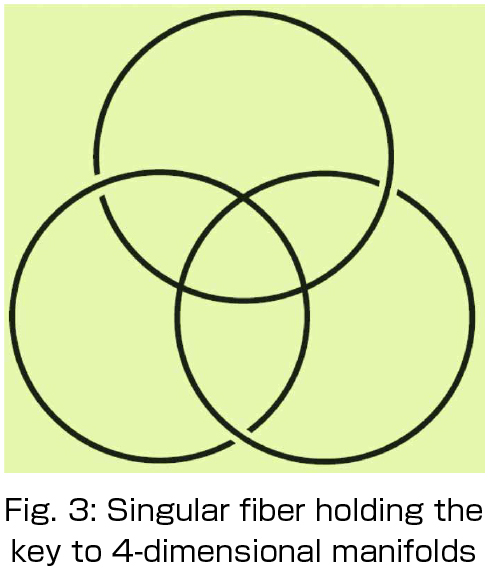
　In addition to knot theory, we are actively investigating singularities of differentiable mappings, using techniques of differential topology. In particular, we have made a number of discoveries for specific cases in which singular points of mappings between smooth objects deeply reflect the topological properties of those objects. I am considered a worldwide authority on the theory of inverse images of points, called singular fibers (see Fig. 3), and I recently published the first book that formulates this theory. More recently, I have been attempting to apply the theory to visual data analysis for multivariate functions. Our group is also interested in analyzing large datasets by employing processes through which the data can be visualized and their characteristics can be grasped in a robust manner. Differential topology plays an essential role in the realization of this project.

　We have also been working on a broad range of topics in topology, including separation properties of codimension-one mappings, topology of isolated singularities of complex hypersurfaces, 4-dimensional manifolds, embeddings in codimension one, and differential geometric invariants of space curves. These studies can be applied in various fields; e.g., they provide powerful tools for studying properties of materials at the microscopic level. In fact, our group has collaborated with industrial firms and found that certain topological invariants can be used to estimate physical properties of hard materials. We have thus found that although topology is a study of soft geometric objects, it can also be used to study hard objects!

　My diverse research has greatly impacted my students. This fact is reflected by the broad range of the research topics studied by my master’s and Ph.D. students. In addition, some of my students have made important contributions to industrial technologies. I am also the coordinator of the WISE program “Graduate Program of Mathematics for Innovation”, nurturing doctoral talents in mathematics.

　I hope that we can continue to strengthen the relationship between mathematics and industrial technologies through application of topology, a branch of pure mathematics.