Discrete Optimization and its Applications

KAMIYAMA, Naoyuki
Degree: Doctor of Engineering (Kyoto University)
Research interests: Discrete Optimization, Graph Theory, Computational Complexity
I carry out research of the theoretical aspects of discrete optimization. My main fields of interest include graph theory and computational complexity, which are deeply related to discrete optimization. These fields lie at the intersection of mathematics and computer science, and there is great interaction between them. The main problem in which I am presently engaged is to obtain a unified understanding of these fields by using submodularity, which is a discrete analogue of convexity and polyhedral approaches based on duality. In the following, I will briefly explain these fields and the problems I am investigating in my research.
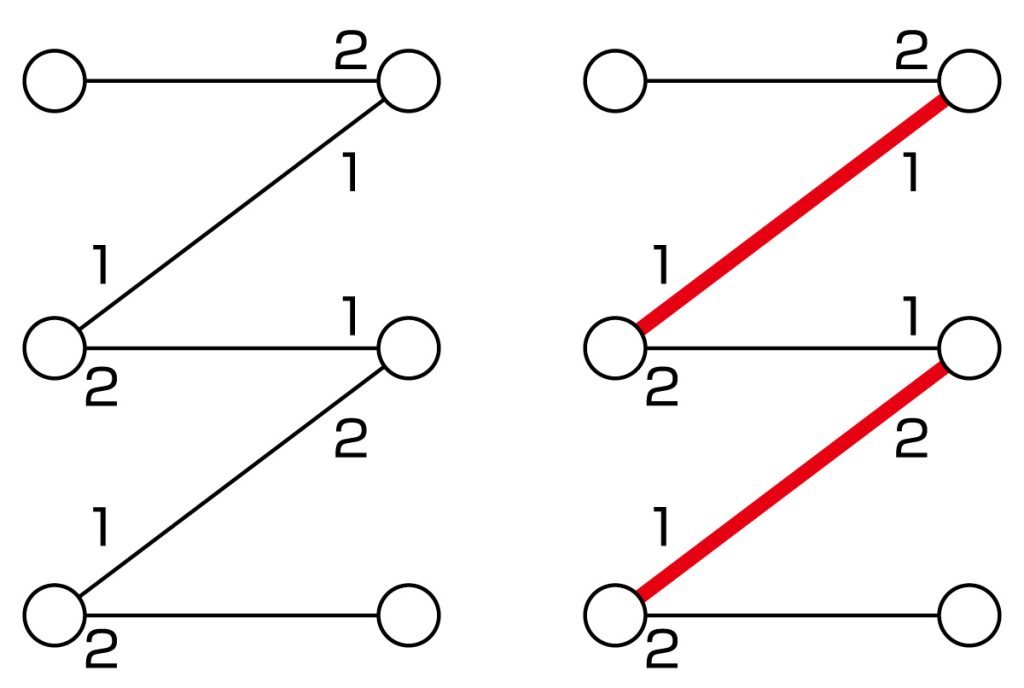
The numbers represent preference lists. (right) An example of an assignment.
Let me first explain discrete optimization. Optimization is the problem of finding a solution that maximizes or minimizes an objective function among all feasible solutions. Discrete optimization deals with optimization problems possessing discrete structures. In this field, we attempt to determine which properties enable us to find an optimal solution without checking all feasible solutions, and we derive methods for finding optimal solutions (called algorithms). I am presently studying stable matching problems, in which one attempts to find an optimal assignment between two groups (see Figure 1). I am also studying network flows that model flow through a network and matroids and submodular functions, which are abstract frameworks for discrete optimization.
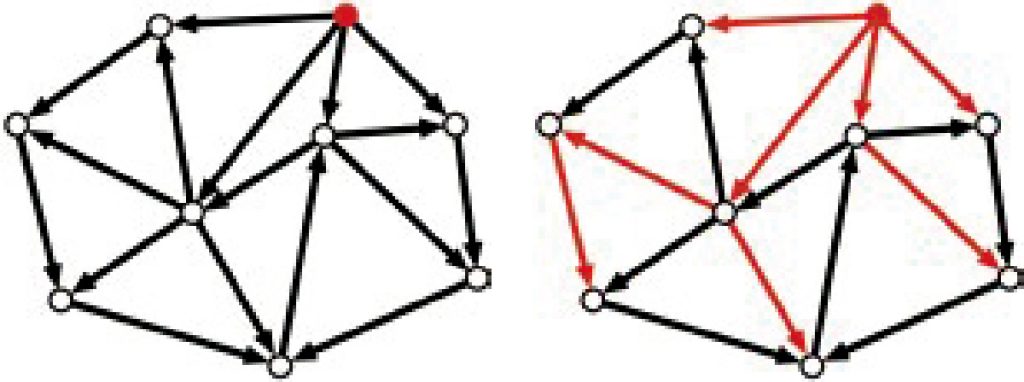
Next, I explain graph theory. A graph consists of vertices and edges connecting vertices. Edges represent topological relationships among vertices (see Figure 2). Intuitively, a graph can be understood as a mathematical model of a road network in an urban area. In graph theory, we try to elucidate general properties of graphs. For example, we attempt to determine whether graphs are sufficiently robustness for some purpose. I am presently studying min-max theorems concerning packing arborescences (see Figure 2) and the edge-dominating set problem, which is one of the most fundamental optimization problems in graph theory.
Finally, I explain computational complexity. Roughly speaking, the goal of the above two fields is to understand what we can do. Contrastingly, the aim of computational complexity is to understand what we cannot do, i.e., the limits of our computational capability. More precisely, in this field we formally define abstract models of computation and study the limitations of these models. The P vs NP problem proposed by the Clay Mathematics Institute is a central problem in this field. At first glance, optimization and computational complexity seem to be, in some sense, opposites. However, there is a deep connection between these fields. Recently, techniques in optimization have been used for analysis in computational complexity. I am interested in the application of optimization techniques (e.g., the polyhedral approach) to computational complexity. I am also interested in applications of optimization techniques to real-world problems arising in urban planning, the design of transportation systems and social networks.

