My research activities are based on the study of integrable systems, which originates from the study of nonlinear waves with a particle-like characteristic called solitons. In mathematics, although fundamental equations to describe solitons are nonlinear partial differential equations, which are generally difficult to analyze, they possess a miraculous property in that they can be exactly solved. Behind such miracles lies the mathematics of infinite-dimensional space with the symmetry of infinite degrees of freedom. A family of functional equations that share this property is called integrable systems. A deep understanding of the underlying mathematics of integrable systems enables various applications. Three such examples follow.

1. Discretization and ultra-discretization: A method to discretize both independent and dependent variables of the soliton equations preserving the integrability has been developed (ultra-discretization). A typical interaction of solitons is shown on the top of Fig. 1, where a large soliton with a higher velocity comes from the left and passes a smaller, slower soliton. An automaton that describes solitons is shown on the bottom of Fig. 1. There are rows of boxes and balls. At each time stop, from the left to the right, each ball is moved to the empty box closest to the right once, and the time is incremented by one when all balls have been moved. This simple model describes solitons, and a sound correspondence to a partial differential equation can be established through ultra-discretization. Discretization and ultra-discretization preserving integrability have been applied to a wide range of mathematical sciences and engineering, including numerical analysis and traffic flow analysis, and this is my theoretical backbone of the collaborated activities with other area, in particular, those related to geometry (discrete differential geometry). Recently, applications of the ultra-discretization have been extended to the non-integrable diffusionreaction systems so that many reaction-diffusion cellular automata have been constructed. In addition, the underlying geometric structure of ultradiscrete systems has recently been clarified in terms of tropical geometry.

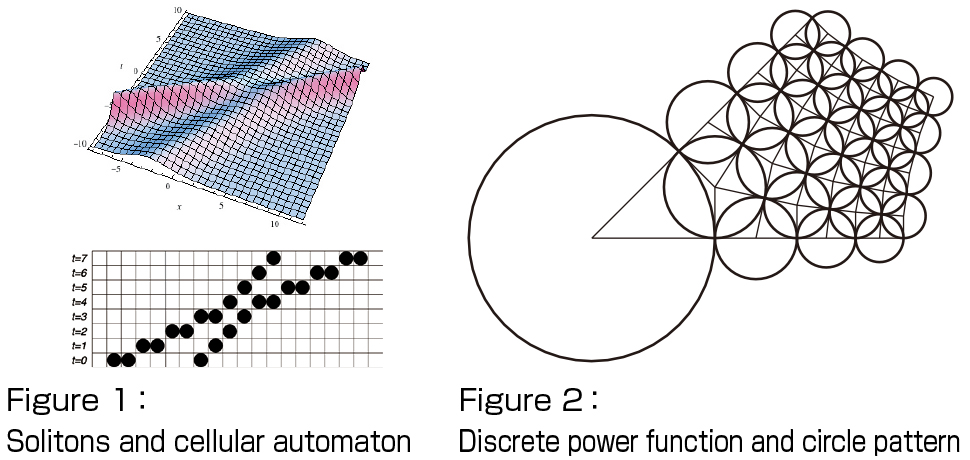
2. Discrete Painlevé equations and elliptic curves: A family of difference equations called discrete Painlevé equations is formulated as an addition theorem on moving pencils of cubic curves in the complex projective plane. Their solutions can be regarded as the generalization of the special functions of hypergeometric type, such as the Bessel functions. On the top of these equations there lies the elliptic Painlevé equation with the symmetry of E₈ ⁽¹⁾ type, and the elliptic hypergeometric function expressible by the elliptic theta functions arises as the particular solutions. This function is considered to be at the top of all the hypergeometric type special functions. As an application, discretization of certain complex regular functions can be described by the (discrete) Painlevé equations. Figure 2 illustrates the discrete power function Z^1/2, where the grid is characterized by the circle patterns.

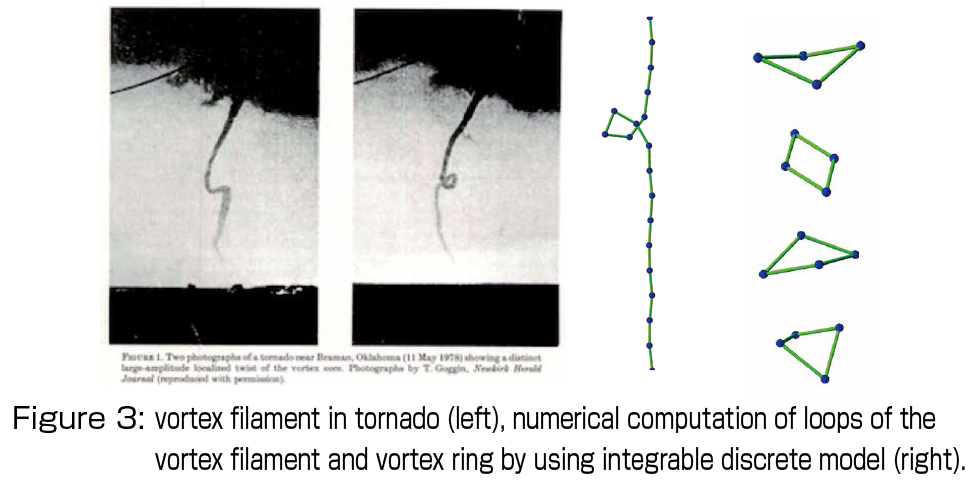
3. Discrete integrable differential geometry and geometric shape generation: Various integrable sytems arise as the fundamental equations describing the space curves and surfaces and their deformations. Further, recently, the theory of curves and surfaces consistent with the discrete integrable systems advanced, so that I am now developing the geometric shape generation, in particular, generation of “good” curves and surfaces in a certain sense, collaborating with the experts of industrial design and architecture. Figure 3 shows the typical dynamics of tornados, namely natural vortex filaments (left), and the results obtained by the integrable discrete model (right). It gives high quality results with low-cost computation since the underlying structure is preserved. Figure 5 (left) is a family of plane curves called the logaesthetic curves which was proposed in Japan as shape elements of CAD with built-in aesthetic property, and they were extracted from the shapes which we think beautiful, such as Japanese swords and butterflies (Figure 4). Recently, we have proposed a new theoretical framework from the standpoint of the integrable geometry, from which we constructed the high-speed and high-quality discretization and a space curve extension (Figure 5 right). We develop this theory to the surfaces, and implement the family of curves and surfaces with aesthetic character as the geometric shape elements, and eventually we aim at standardization of those shape elements in the area of industrial design. Those shapes would serve as important examples of mathematical models incorporating the element of human feeling of “aesthetics”: Good equations can generate good shapes.