私は可換環論と組合せ論が交錯する分野で研究をしています。いくつかの分野が交錯している分野の面白さに, 一つは様々な観点から物事を捉えることができるというのが挙げられます。例えばパスカルの三角形(図１)を考えます。パスカルの三角形は, 一行目に1, 二行目以降各行の両端に1, それ以外は左上と右上の和と帰納的に定義されます。このときパスカルの三角形に現れる行と二項係数の列が対応することはよく知られています。図2を参照してください。また, パスカルの三角形の各行と単体の各次元面の個数が対応しています。ただし, 単体の次元面の個数の列は-1次元面から始まっているとし, -1次元面の個数は1と定義しています。単体とは点, 線分, 三角形, 四面体などを一般の次元に拡張した概念です。図3は四面体です。四面体の各次元面の個数の列がパスカルの三角形の5行目に対応していることを確認してみてください。

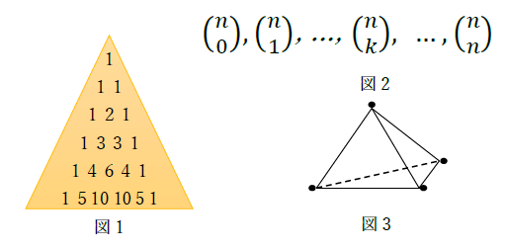
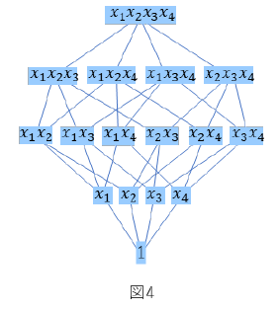
　二項係数についてもう少し掘り下げていきましょう。図2にあるような二項係数の列は対称的(回文的)です。これは二項係数の定義から直ちに証明することができます。二項係数は様々な分野においてしばしば現れる基本的なものです。二項係数の列は対称的(回文的)であることを可換環論の観点から証明してみます。環 A=k[x₁, x₂, …, x_n]/(x₁², …, x_n²) を考えます。この環は次数付環となり各斉次空間はベクトル空間となります. n 数からk 個選んだ, $(^n_k)$個のsquarefree単項式たちが, Aのk次斉次空間の基底になっています。つまりAの各斉次空間の次元が二項係数となっています。単項式の割る割られるという関係を半順序として、環Aの基底たちは半順序集合となります。図4はn=4の場合のHasse図です。環Aは対称性の良い環であるGorenstein環になっています。詳細は省きますがそういった対称性から二項係数の列は対称的(回文的)であることが示されます。実はもっとよいことに二項係数の対称性だけではなく他の性質もわかります。

　二項係数を例に可換環論と組合せ論の交差点を見ましたが, そういった例は他にもたくさんあります。また, 可換環論と組合せ論に限らず様々な分野の交差点がありそこから分野が日々発展しています。分野の交差点で研究することの難しさは様々な分野の知識を必要とすることが挙げられますが多くの気付き・発見があります。こういった気付き・発見を標識にしてこれからも研究を頑張っていきたいです。