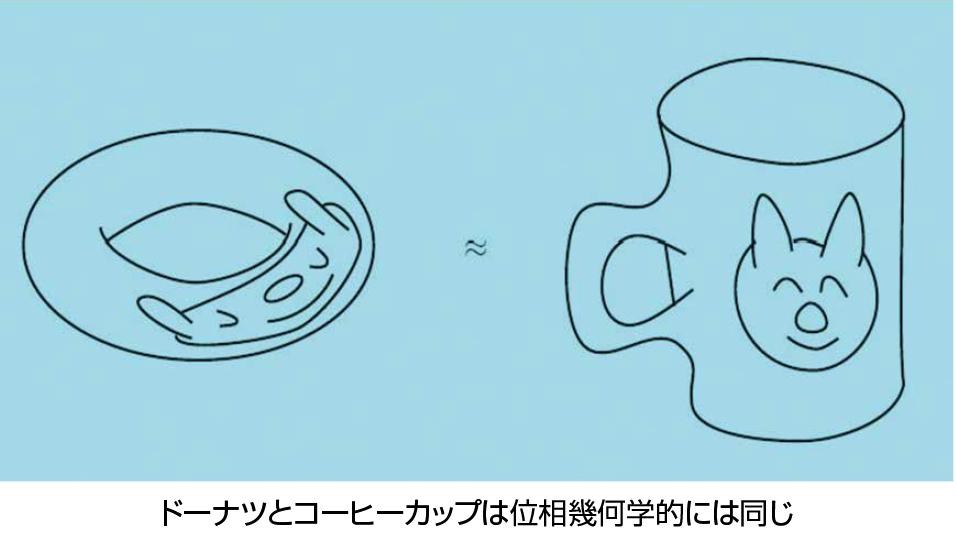
位相幾何学（トポロジー）とは、図形をゴムのようなものでできていると考え、グニャグニャと連続的に変形できるものは同じと思う、とても柔らかい幾何学のことです。言い換えると、幾何学的対象の性質のうち、それを連続的に変形しても変わらないものを研究する、純粋数学の一分野です。たとえばコーヒーカップとドーナツは位相幾何学的には同じものと考えられます。それらには「穴」がちょうど１つずつありますが、この「穴」の個数は、図形の連続変形で変わらない量の１つの典型的な例となっています。

　こうした位相幾何学は、図形が柔軟性を持つ場合に威力を発揮します。その最たるものが、紐を結んでできる結び目や絡み目です。紐を結ぶことは日常生活でも重要な行為で、結び目が原始時代から人間の生活と深く結びついていることは間違いありません。実際、野生のゴリラも結び目を作ることができることが知られています。ごく最近になって、こうした結び目が、DNA（デオキシリボ核酸）の研究に深く関わることが明らかになってきています。

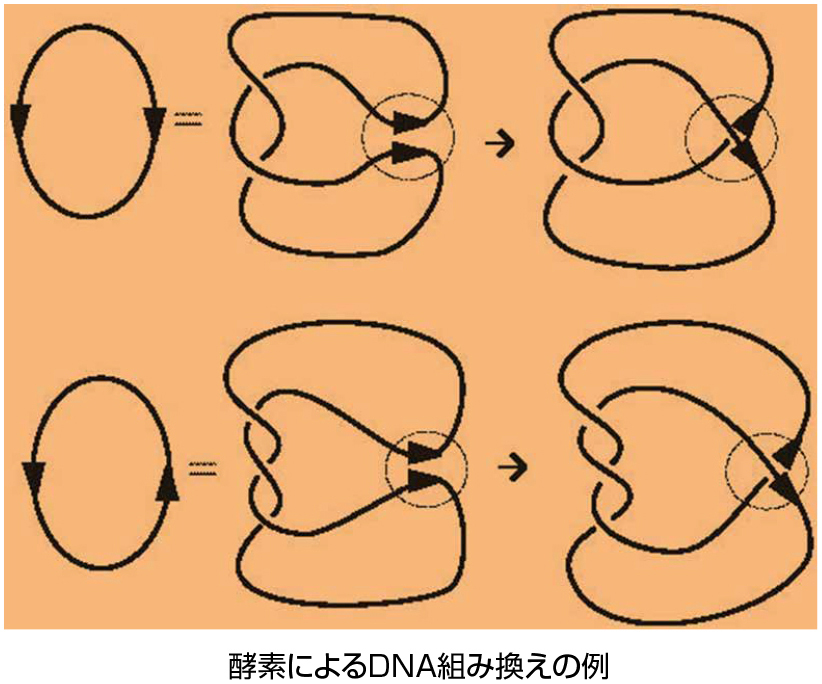
　遺伝情報の担い手であるDNAは、生物の細胞内で捩れた紐状の形をしていて、輪になっていることもあり、さらにそれが結ばれたり絡んだりしていることもあります。こうしたDNAの結び目・絡み目は、酵素の働きによって作られることは知られていましたが、その仕組みの詳細については実験技術の限界のために明らかにされていませんでした。1980年代終盤、数学者のC.ErnstとD.W.Sumnersは、数学、特にトポロジーにおける結び目理論の最新の結果を駆使してその酵素の仕組みを解明しました。もともと結び目理論は19世紀のGaussによる電磁気学やKelvin卿による渦原子仮説に端を発すると言われていますが、その後化学者・物理学者は結び目を忘れ、数学者だけが興味を持って研究してきた歴史があります。我々はその流れを受け、現代数学の中でも最近もっとも盛んに研究されている分野の１つである結び目理論を駆使することにより、トポイソメラーゼと呼ばれる酵素によるDNA組み換えの解析を、数学的側面から研究しており、こうした解析の産業技術への応用も目指しています。

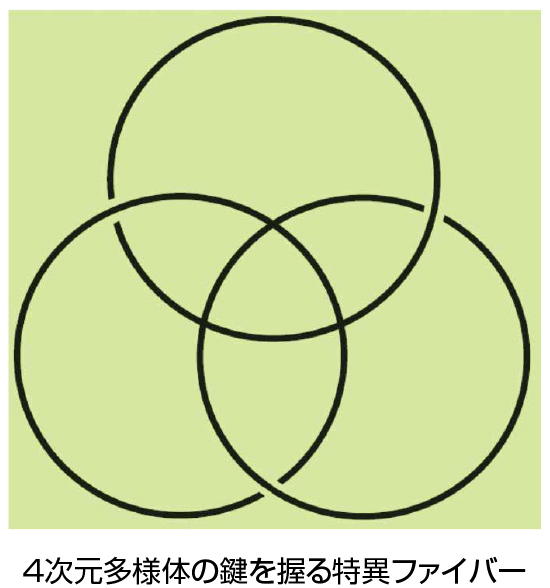
　なお、こうした研究と同時に、可微分写像の特異点論も活発に研究しています。特に、滑らかな物体間の写像の特異点が、そうした物体の位相幾何学的性質を深く反映する具体的事実などを数多く発見してきています。特に、特異ファイバーと呼ばれる1点の逆 4次元多様体の鍵を握る特異ファイバー像に着目する研究では世界的な第一人者を自負しており、それを最初に定式化した著書も出版しました。最近はこうした理論を、多値関数データのための視覚的解析に応用すべく、研究を行っています。

　また、可微分写像の特異点論以外にも、位相的埋め込みの第一障害類、余次元1写像の分離性質、複素超曲面の孤立特異点の位相幾何、ファイバー結び目、4次元多様体、余次元1の埋め込み、空間曲線の微分幾何学的不変量、結び目解消数など、位相幾何学の様々な分野を幅広く研究しています。こうした研究は、種々の分野で応用できる可能性があり、たとえば物質・材料の性質をミクロなレベルから考察する際には威力を発揮することが期待されます。なお、一般化されたフィボナッチ数列の漸近挙動についても精力的に研究を行っており、解析関数の零点に関する研究もあります。

こうした幅広い研究を行っていることは、教育に対する効果もかなり大きく、これまでに指導した学生の産業技術への貢献実績もあります。また、異分野連携で活躍する数学博士人材を育成するための卓越大学院プログラムのコーディネーターも務めております。

　今後も、トポロジーという純粋数学を基に、数学と産業技術の関わりを深めてゆければ誠に幸いです。