ルーレット，双六，宝くじ，株価の値動きなど，確率的現象は日常生活においても身近に観察できるものです．これらの現象(対象)には自然に確率的な要素が備わっていますが，一見ランダムな要素がまったくないように見える問題にもランダムな側面があったり，意外な形で確率論的手法が使えることがあります．ここではそのような例を3つばかり紹介します．

(1)日本では「角谷予想」，海外では「コラッツ予想，3n+1問題」などと呼ばれる初等整数論の有名な未解決問題をご存知でしょうか? 任意に選んだ自然数に対して，「自然数が偶数ならば2で割り，奇数ならば3をかけて1足す」という操作を繰返すと必ず最後は1になるという予想です．例えば，初めに7を選んだとすると，7，22，11，34，17，52，26，13，40，20，10，5，16，8，4，2，1となります．2009年の時点で20×2⁵⁸以下の自然数に対しては，コンピュータによって予想が正しいことが確かめられています．この問題自身にはどこにも確率的要素はありませんが，実はランダムな構造が潜んでいます．

(2)以下の文字列は，単純換字暗号とよばれる古典的な方式で，ある文章を暗号化したものです．つまり，aをf に，bをtにというように，aからzの順番を入れ変えて一対一に対応させることによって暗号化しています．

fyeaxj​qfzjoxc​eddedc​jbujcx​bjhxg​pjbeg​xrjukj​zebbe​dcjop​jsxgjz​ezbxg​judjbs​xjofd​ljfdrju​kjsfhe​dcj

暗号化の方法が上の方式であるとわかっているとすると，マルコフ連鎖という確率論の基本的な道具で(ある程度)解読することができます．以下はその実行例です．

Googleなどの検索サイトの人気ページのランク付けにもマルコフ連鎖が使われていることはよく知られています．

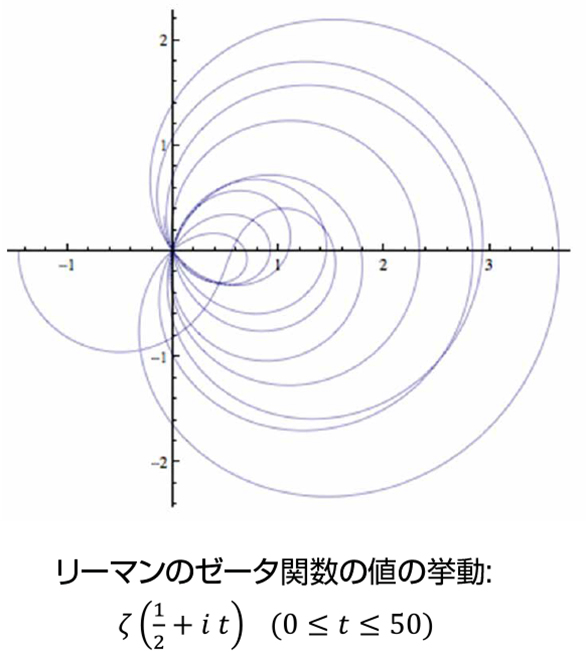
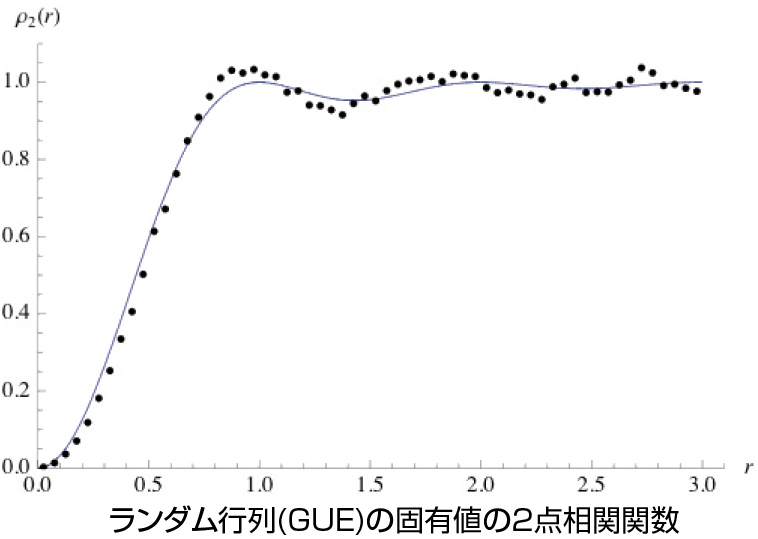
(3)2000年にアメリカのクレイ数学研究所が，ミレニアム問題として100万ドルの懸賞金をかけて7つの問題を提出しました．そのうちの一つであるポアンカレ予想は最終的にはペレルマンによって解かれましたが，いわゆるリーマン予想は未解決の難問です．リーマン予想とは，$\zeta (s)=\sum ^{\infty }_{n=1}\frac{1}{n^s}$ で定義されるリーマンのゼータ関数とよばれる複素関数の（非自明な）零点はすべて Re$(s)=\frac{1}{2}$ という線上にあるだろうという予想です．この問題にもランダムな要素はまったくありません．しかし，多くの理論的考察やシミュレーションなどにより，その零点達があるランダム行列の固有値と同じ振る舞いをすることがわかってきています．

私の興味の一つは，上に挙げたような一見ランダムには見えない現象の裏に潜むランダムな現象を見つけて，それを確率論的手法を用いて研究することです．

(1)の問題は1960年代に数学者の角谷静夫先生が興味を持たれて，イェール大学の同僚に伝えたところ，イェールの数学教室では一ヶ月くらいの間皆がこの問題に嵌ってしまったそうです．他の大学でも同じような現象が起こり，一時期流行ったゲーム「テトリス」と同じように，数学の研究を鈍らせるための某国の陰謀だったのではないかという笑い話もあったそうです．

(2)であげた問題は，アメリカのある州立刑務所の囚人の書いた壁の落書きが何を意味するのかを調べるために，刑務所の心理学者によってスタンフォード大学統計学教室の技術相談窓口に持ちこまれたことがきっかけだっただそうです．

(3)の研究の方向性は，プリンストン高等研究所のコモンルームでのティータイムに，物理学者であるダイソンから解析数論の研究者であるモンゴメリーへ述べられた一つのコメントから始まりました．数学者レンニは，「数学者とはコーヒーを定理にかえる機械である」と言ったそうですが，一杯のコーヒー(紅茶?)が重要な研究の方向付けをした場面でした．

　IMIにおいても，自由な発想により実りある異文化間の交流ができることを心から願っています．