Universal logic is a general study of logical structures with no commitment to any particular logical system in the same way that universal algebra is a general study of algebraic structures. The term “universal” refers to the collection of global concepts that allow one to unify the treatment of the logical systems and avoid repetition of similar results. One major approach to universal logic, in terms of both number of research contributions and significance of the results, is institution theory. This relies upon a category-based definition of the informal notion of logical system, called institution, which includes both syntax and semantics as well as the satisfaction relation between them. As opposed to the bottom-up methodology of conventional logic tradition, the institution theory approach is top-down: the concepts describe the features that a logic may have and they are defined at the most appropriate level of abstraction; the hypothesis are kept as general as possible and they are introduced only on by-need basis. This has the advantage of proving uniformly results for a multitude of logical systems. It leads to a deeper understanding of the logic ideas since the irrelevant details of particular logics are removed and the results are structurally obtained by clean causality. My research interests cover, roughly, institution theory and its applications to computing science.

(1) Foundation of system specification and verification

There are many contributions of institution theory to computing science, the most visible one is providing mathematical foundations for the formal methods techniques, i.e. specification, development and verification of systems. In algebraic specification, one of the most important classes of formal methods, it is a standard and mandatory practice to have an institution to underlie each language basic feature and construct; institution theory sets a standard style for developing an algebraic specification language that initially requires to define a logical system formalized as an institution and then develop all the language constructs as mathematical entities in the framework provided by the underlying institution.

(2) Reconfigurable software systems

The main direction of my research consists of developing logical structures supporting the efficient development of correct reconfigurable software systems, i.e. systems with reconfigurable mechanisms managing the dynamic evolution of their configurations in response to external stimuli or internal performance measures. A typical example of reconfigurable system is given by the cloud-based applications that flexibly react to client demands by allocating, for example, new server units to meet higher rates of service requests. The model implemented over the cloud is pay-per-usage, which means that the users will pay only for using the services. Therefore, the cloud service providers have to maintain a certain level of quality of service to keep up the reputation. Generally speaking, reconfigurable systems are safety- and securitycritical systems with strong qualitative requirements, and consequently, formal verification is needed.

(3) System development

I am currently maintaining the Constructor-based Theorem Prover (CITP), a proof management tool built on top of an algebraic specification language for verifying safety properties of transition systems. The methodology supported by the tool is not intended for formalizing mathematics, but for the application to the development of software systems. In order to achieve the targeted goal, the following important research directions are pursued:

(a) proposing more expressive logical systems to allow engineers to specify easily and accurately the software systems,
(b) develop decision procedures that can reason efficiently about these more sophisticated logics, and
(c) improvements of the proof assistant interface to help the user understand the current state of the proof and interact with the tool in a more natural way.

The interest is in the design of software systems as one can see in the table below.

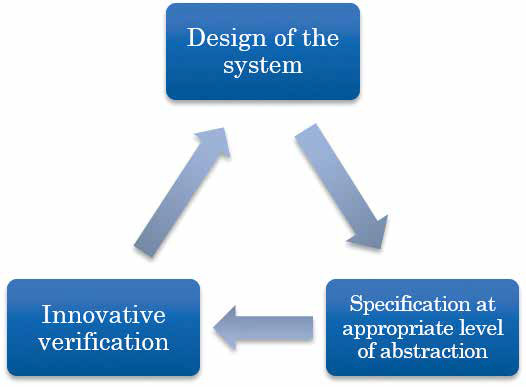
The system will be specified at the most appropriate level of abstraction depending on the requirements for its behavior. The result of the verification performed with the tool will determine if improvements of the design are required or not.