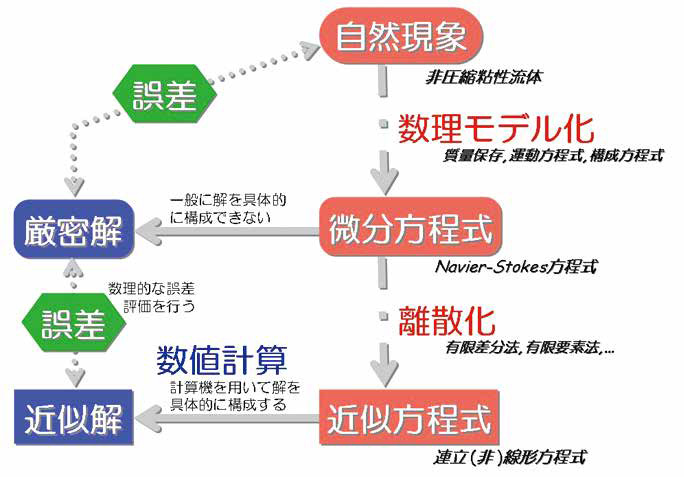
水の流れや熱の伝達など，自然界や産業界で見られる様々な現象を，計算機を用いた数値シミュレーションによって理解することに興味を持っている．数値シミュレーションでは，まず現象を物理法則に基づいて微分方程式で記述する“数理モデル化”を行い，次に微分方程式を計算機で扱うことのできる近似方程式に置き換える“離散化”を行い，最後に近似方程式の解法を計算機に実装し目的とする現象を再現する“数値計算”を行う(図1参照)．我々は，提案する“離散化”手法が本来の現象に対する“精度の良い”離散化になっているか，実用に耐えうる“効率の良い”離散化になっているか，を数理的に検討する研究に取り組んでいる．また様々な問題に対して，提案する“離散化”手法に基づいた“数値実験”を実際に行い，自然現象の理解や工業製品の設計へ応用することにも取り組んでいる．

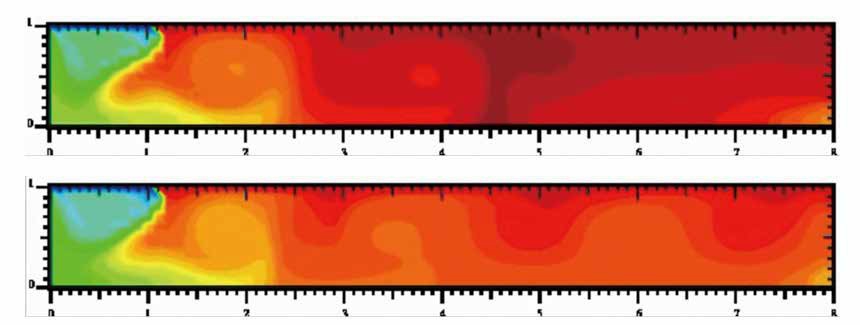
我々が取り組んでいる研究の一つに，ガラス溶融炉内部におけるガラス原料の流動や熱伝達の数値シミュレーションがある(図2参照)．ガラス溶融炉内部にある高温(約1,500℃)のガラス原料は非圧縮粘性流体と見なせることから，溶融炉内部における現象は温度依存係数を持つ熱対流方程式によって数理モデル化できる．我々は時間方向に後退Euler法を，空間方向に混合型適合有限要素法を用いて得られる近似方程式の解に対する最適な誤差評価を導いた．またこの成果を発展させ，ガラス溶融炉の最適設計を行う際の指標の1つである炉全体の熱収支計算に対して整合流束法に基づく離散化手法を提案し，熱収支計算に対する最適な誤差評価を導いた．我々の誤差評価は，境界積分で定義される物理量を直接計算するよりも整合流束法を用いて領域積分に置き換えて計算した方が高精度である，という事実の数理的正当化に対応している．このように数理的正当化した離散化手法に基づく数値シミュレーションを用いて，製品品質の維持とエネルギー消費の抑制を両立したガラス溶融炉の最適設計について検討を試みている．

その他に我々が取り組んでいる研究の一つとして，変圧器内部の渦電流に代表される磁場の数値シミュレーションがある(図3参照)．複雑な形状を持った領域や変化の著しい現象の数値シミュレーションを精度良く行うためには，自由度数が10⁷(あるいはそれ以上)の近似方程式を効率良く扱うことがしばしば要求される．我々は静磁場問題に対して，既知量である電流密度の補正を考慮した混合型定式化による数理モデルを導入した．この数理モデルに対して反復型領域分割法に基づく近似方程式を提案し，さらに混合型定式化の際に現れるLagrange乗数の性質を利用した簡略化を行った．提案した手法は，必要となる行列ベクトル積演算を部分領域ごとに独立な静磁場問題を解くことに帰着できるため，計算効率向上のために用いられる並列計算に適しているという利点がある．以上のことから，提案した手法に現れるある反復計算の収束特性が改善され，計算効率が向上した．これにより，従来は解くことのできなかった大自由度モデルの解析に成功した．このように効率化した離散化手法に基づく数値シミュレーションを用いて，磁場の振る舞いをより精度良く把握することを通して，変圧器の最適設計についての検討を試みている．

さらに我々は，粘弾性流れ問題，移動境界流れ問題，光波の干渉・散乱問題などの数値シミュレーションにも関心を広げて研究を続けている．これにより，数理的正当化がなされた数値シミュレーションがより多くの現象に対して可能になると期待できる．