The main focus of my research work is on rigorous mathematical modeling and analysis of multiscale and multiphysics systems in materials science. My investigations explore ways information and disorder emerge and evolve generating complexity and patterns in smart materials such as martensite, nematic elastomers and liquid crystals. Understanding the microscale features and mechanisms of multifunctional materials and predicting their interactions on the overall macroscopic properties is of strategic importance in the design of materials for engineering applications. Two specific lines from my past and current research are summarized below.

1) Solid-to-solid phase-transformations in shape-memory alloys

　Austenite-to-Martensite phase transformation is observed in various metals, ceramics and biological systems. It is the activation mechanism of the Shape-Memory effect. Despite the vast potential to the shapememory effect, practical implementations have been slow, and to-date, mostly limited to NiTi. It is strategically important to improve and stabilize the shape-memory effect in known materials and develop new modeling strategies. A problem I have considered is the analysis and modeling of disclinations (topological defects at the lattice level characterized by rotational mismatch). Disclinations as in Fig. 1-a are characterized by a self-similar triple-star pattern resulting in intense rotational stretches. Mathematically, I have shown that such configurations arise as a solution of differential inclusion problems with special rotational symmetry and rigidity. By identifying the basic algebraic structure underlying the differential inclusion I have computed exact solutions both in linearized and finite elasticity models shedding light on the mechanism that drives formation of triple-stars. Moreover, I have investigated onset of criticality and self-organization in the evolution of martensite via sequential avalanching. Here the modeling strategy describes the nucleation of martensitic variants as a branching random walk process (see Fig. 1-b). The question that I addressed is the behavior of certain features of the self-similar structure thus formed and the computation of power laws for the length interfaces in a martensitic transformation. This project involved collaboration with the groups of J. Ball and B. Hambly (Oxford, stochastic modeling of martensite); E. Vives and A. Planes (Barcelona) and T. Inamura (TiTech) on experiments on avalanches and disclinations in martensite. Work is in progress on the investigation of the activation mechanisms that drive avalanches in metals with the ultimate goal of mechanically characterizing the dynamics of solid-to-solid phasetransformations.

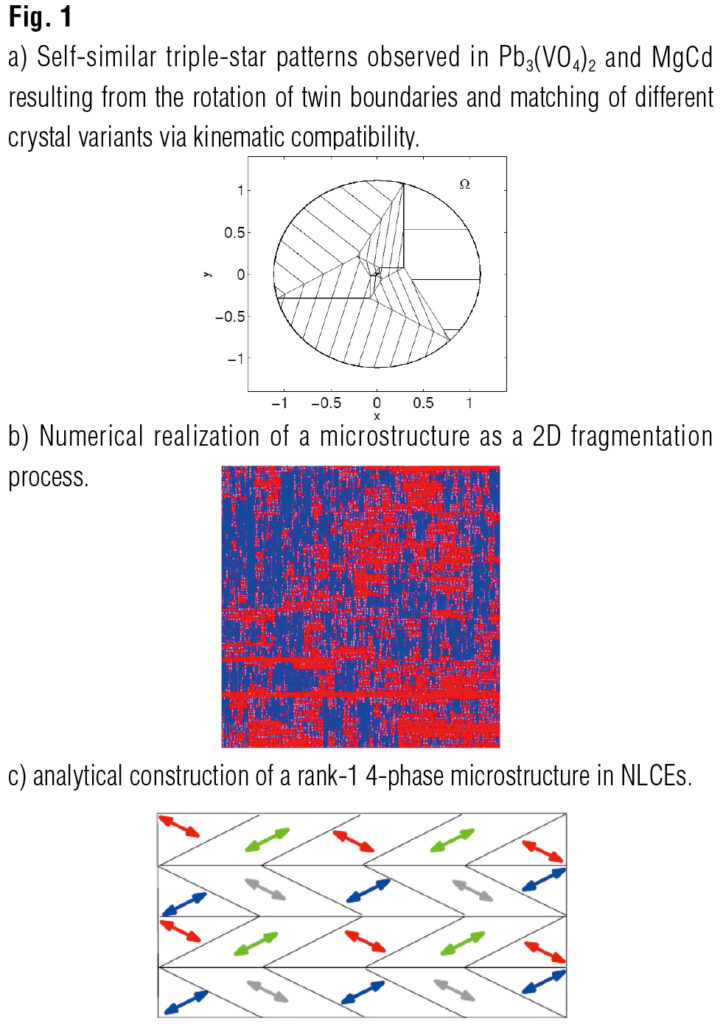
2) Homogenization and Gamma-Convergence problems for nematic elastomers

　Nematic Liquid Crystal Elastomers (NLCEs) are a class of soft ShapeMemory Alloys that combine the entropic elasticity of a network of crosslinked polymeric chains with the peculiar optical properties of nematic liquid crystals. A thorough understanding of the manipulation of optical birefringence in thin-films of NLCEs by mechanical, electric and thermal means is a tremendous mathematical task which has strategical potential applications in materials design and fundamental sciences. Focusing on the strain-order coupling in NLCEs, I have investigated mechanisms that rule the low energy states in mechanically and geometrically constrained systems such as artificial muscles, sensors and actuators. The mathematical language required to tackle NLCEs problems is that of calculus of variations, Gamma-convergence and relaxation. These are sophisticated techniques at the intersection of the analysis of PDEs, functional analysis and measure theory based on energy minimization approach and which are particularly suitable for the study of singularly perturbed variational problems. Collaborations are in progress with the experimental Lab of K. Urayama (KyotoTech).