私は主に数論的不変式論と呼ばれる分野を中心として研究活動をしています。大枠としては代数学の中の数論に属する分野です。その動機と手法から紹介します（図1）。

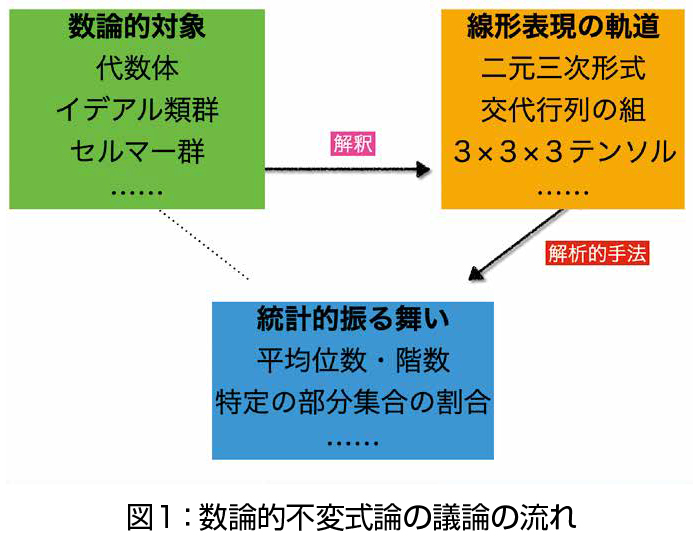
　まず興味の対象は、代数体やそのイデアル類群、（有理数体上の）楕円曲線のモーデル・ヴェイユ群など、数論において重要だが扱いの難しい対象です。代数体や楕円曲線は無限に存在し、それぞれ例を作れと言われると比較的簡単に構成できます。しかし個々の例に対してイデアル類群やモーデル・ヴェイユ群を計算することは、しばしばかなり難しくなります。そしてパラメータを少し変更するとそれぞれの量は大きく変わります。
　そこで、個々の例ではなく、代数体や楕円曲線全体を考えたときにイデアル類群などがどう振る舞うか、という問題を考えます。たとえばイデアル類群の『平均』位数や、モーデル・ヴェイユ群の階数が大きい楕円曲線の『割合』などを問題にします。こうした問題意識を持つ研究は総じて数論統計と呼ばれ、数論幾何、表現論、ランダム行列の理論などと結びつきながら発展しています。数論的不変式論の主な結果である M. Bhargava と A. Shankar の結果も、モーデル・ヴェイユ群の（高さに関する）平均階数の上界を与えるものです。
　次にその手法です。まず数論的対象を、より取り扱いやすい代数群の線形表現の軌道として解釈します。この解釈を踏まえると、数論的対象の数え上げの問題が、ある基本領域中の格子点の数え上げに帰着される場合があります。そうした場合には、解析数論の技術と結びつけることで、もとの数論的対象についても平均・割合などが議論できるのです。私もこの流れを踏まえて、有理数体上の平面三次曲線のなかで、線形行列式表示と呼ばれる表示を持つものの割合を研究しました（例：図2）。

　関連した別の研究として、ある数論的な性質を満たす曲線などの具体例を構成したり、あるいは具体的に与えられた曲線の性質を計算する研究も行っています。

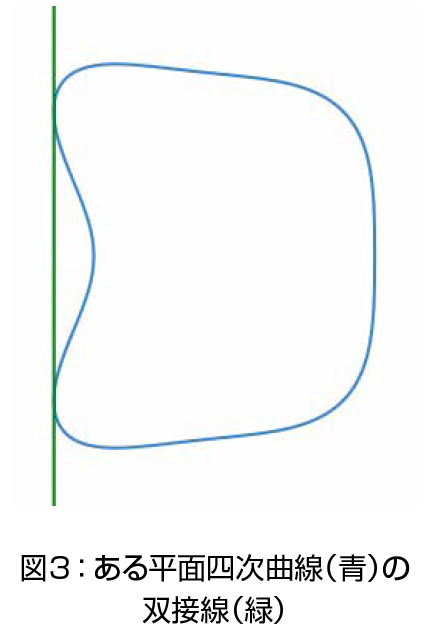
　その一例が、平面四次曲線の双接線についての研究です。平面四次曲線の双接線は、その曲線と二点で接する直線、あるいは一点で四重に接する直線を指します（図3）。平面四次曲線が有理数係数で定義されていても、双接線が有理数係数で定義できるとは限りません：たとえば虚数が係数に必要かもしれません。伊藤哲史氏、大下達也氏、谷口隆氏、内田幸寛氏との共同研究では、より強く双接線が局所大域性を満たさない有理数体上の平面四次曲線を構成しました。実数やp進数の範囲では双接線が見つかるものの、有数係数では見つからない曲線です。

　こうした方向性では、平面三次曲線の変曲点についても同様の考察を行っているほか、フェルマーの四次曲線についてその法を四としたガロア表現の決定も行っていま す。手法としては近年の結果を利用した数論幾何的な考察とともに、代数的な計算に数式処理ソフトを活用することで結果を得ています。

　これらに通底するのは、代数幾何や不変式論の古典的な問題意識が、数論的な設定で新しい意味を帯びる点です。たとえば数論的不変式論で用いられた数論的対象と表現の軌道の対応の一部は、複素数体だと非常に単純な対応になってしまい、構造が却って見にくくなります。私はそういった数論的な設定で現れる構造について、数式処理の助けを借りながら研究を続けています。