私の主要な研究領域は，広義には理論計算機科学です．その関連で最近は特に代数的言語理論と古典類体論の融合領域の研究に取り組んでいます．

（1） 代数的言語理論

代数的言語理論は形式言語理論の一領域で，歴史的には言語（＝有限文字列集合）の計算階層分類の関連で1960年代から発展してきたものです．例えば我々は素朴に言えば「２進数1101110110101が素数であるか」を判定するのが難しいと感じ，一方で「1101110110101の中に含まれる0の個数は3の倍数か」を判定するのは容易であると感じますが，それは何故でしょうか？ 形式言語理論（或は計算複雑性理論）ではこのような「有限文字列の性質を判定する問題の難しさ」に正確な（Turing機械の実行ステップ数などによる）定義・指標を与え，その難しさの階層を分類することを一つの主要な関心としています．

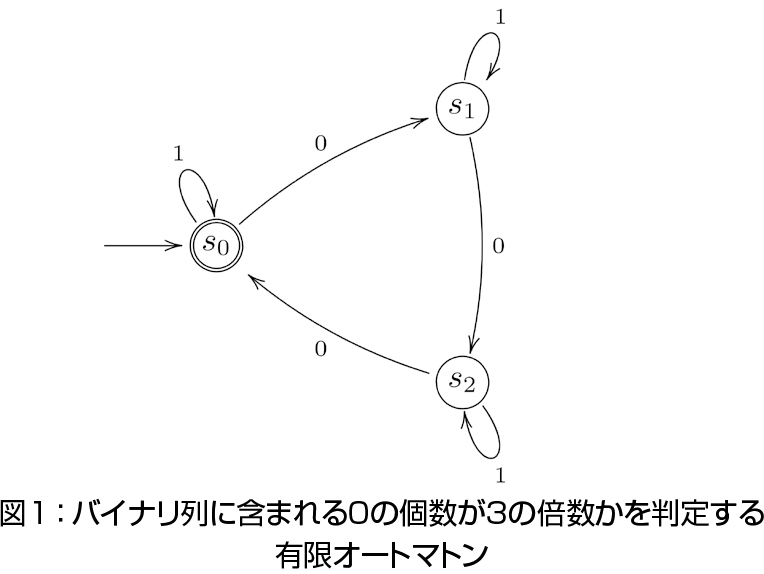
代数的言語理論はこのような言語の研究の中でも，代数的な手法を援用することを特徴としています．特に有限オートマトンによって受理される言語である正規言語に限定して言えば，有限半群論の手法を援用した美しい分類理論（Eilenberg理論）が知られており，私の研究もこの正規言語の分類理論に関わります．

Eilenberg理論の内容を端的に言い表す良い例は，正規言語の論理的表現に関する問題で，1965年にSchützenbergerが証明した定理です．正規言語は一般にBüchiのMonadic Second-order Logic （MSO）という論理体系の論理式で表現できることが知られていましたが，MSOのうち一階の量化子のみを使う部分体系（FO）で表現できる正規表現を特徴づける問題が1960年あたりに興味を持たれていました．Schützenbergerはこの特徴付けを，有限半群論の手法を用いて与え，それがEilenberg理論の出発点となります．Schützenberger以降も正規言語に関する組合せ的・数理論理学的決定問題が，有限半群論の問題に帰着させて解決できる場合のあることが発見されました．その方法を体系化したものがEilenberg理論です．現在では以下の図のように正規言語の様々な階層は，有限半群（モノイド）の階層と自然に対応することがわかっています（双対性）：

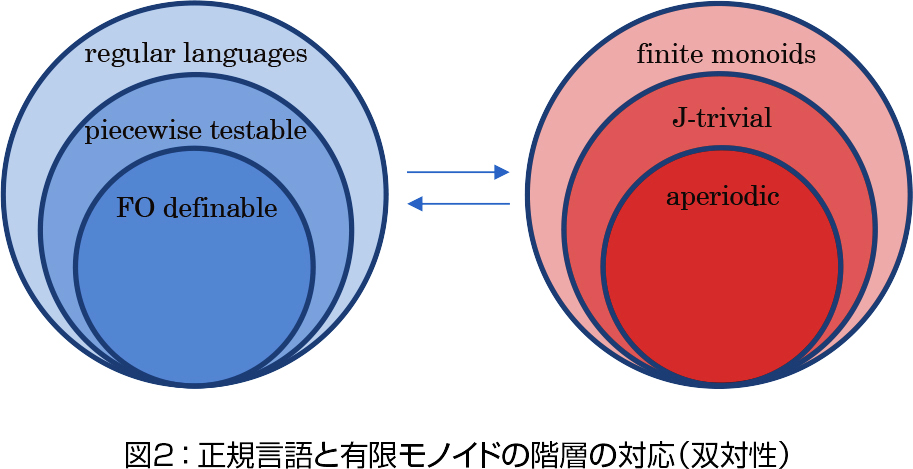
（2） Galois理論・古典類体論との遭遇

Schützenbergerの定理は，技術的には次のように主張します：「正規言語LがFOで定義できるための必要十分条件は，Lから構成される有限統語的モノイドM（L）が非自明な部分群を含まないこと（= aperiodic）である．」簡単にいうと，正規言語がFOの論理式という特定の表現形式で記述できるための必要十分条件を，それに対応する有限モノイドM（L）の純半群論的性質で特徴づけられるということです．

この現象は代数学においてGaloisが示した次の主張と似ていないでしょうか：「多項式f（z）の根が四則演算とベキ根で表されるための必要十分条件は，f（z）の最小分解体Kのガロア群Gal（K/Q）が可解であることである．」実際，この類似はただの類似ではなく，圏論と呼ばれる抽象的な言葉を使って正当化することができ，その結果としてEilenberg理論とGalois理論とは正確な意味で統一することができます．そしてさらにこの統一は，代数体のアーベル拡大の分類や，アーベル拡大での素数・素イデアルの分岐を記述する類体論に対しても，興味深い見方を与えることがわかってきました．現在はこの観察を進め，古典的な代数的言語理論のアイデアと，明示的類体論や非可換類体論との関連づけを模索しています．