Topological Data Analysis and Machine Learning

Keunsu KIM
Degree: PhD (Mathematics) (POSTECH)
Research interests: Topological data analysis, Topological optimization
My primary research interest lies in the intersection of Topological Data Analysis (TDA) and Machine Learning (ML). In particular, I am currently focused on topological optimization.
Topology is the study of continuous objects, known as topological spaces, and the properties that remain invariant under continuous deformation. One of the most well-known invariants is homology, which quantifies the “holes” in a space and can be efficiently computed using linear algebra.
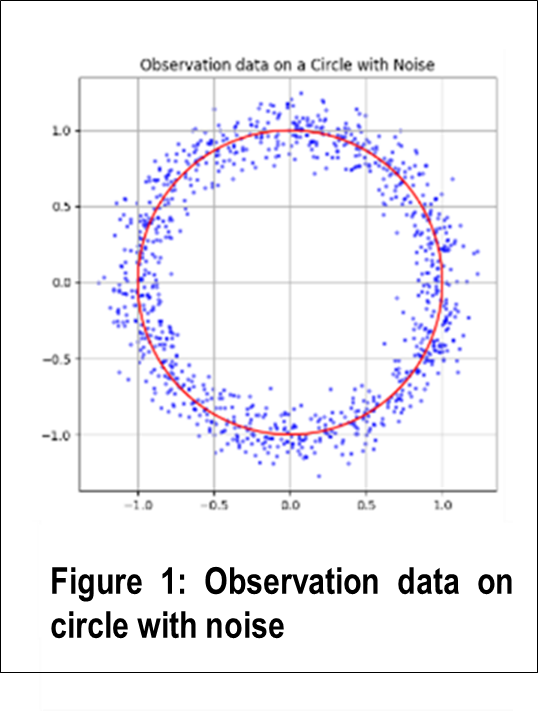
However, a fundamental challenge in data analysis is
that real-world datasets are inherently discrete and
lack meaningful topological properties. For instance,
in Figure 1, the observed data (blue points), sampled
from a red circle, do not form a continuous structure.
The goal of TDA is to infer the underlying continuous
shape (the population manifold) from these discrete
observations.
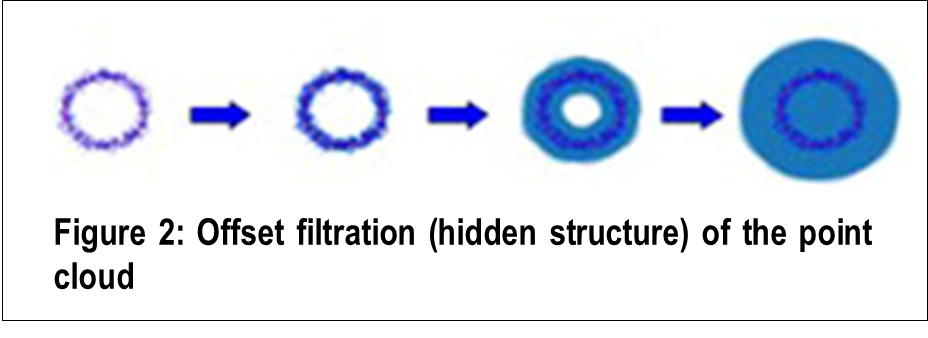
Traditionally, metric information has been used to construct hidden structures from data through methods such as offset filtration (Figure 2) or Vietoris-Rips filtration, and by analyzing these structures, one can infer the underlying continuous shape. It is known that if data is sufficiently and uniformly sampled from a manifold, observing the changes in homology at each step in the hidden structure (persistent homology) allows us to infer the homology of the original manifold.
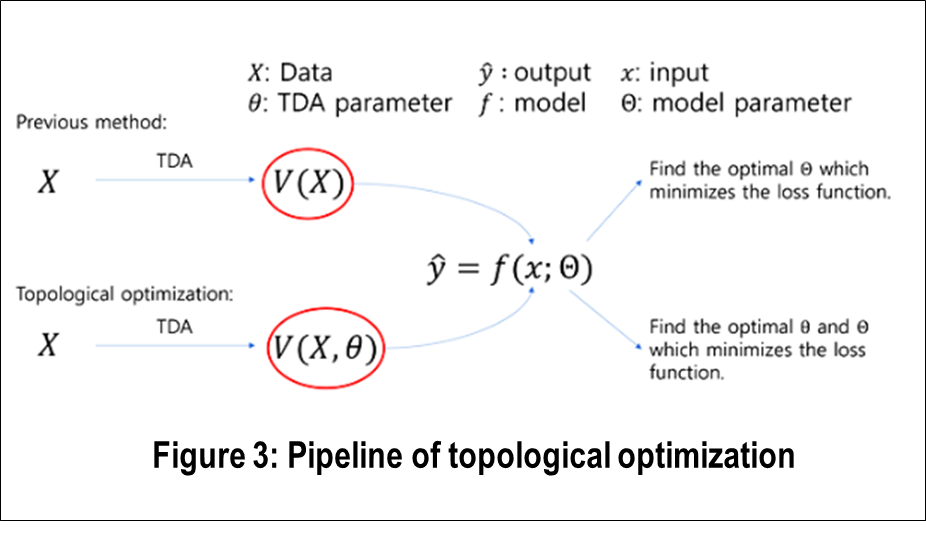
Since the 2020s, interest in topological optimization has grown, with ML playing a crucial role in the TDA process to better capture data characteristics. As shown in Figure 3, the ML model f includes the TDA parameter θ. This emerging paradigm enables a more flexible and data-driven approach to extracting topological information more effectively.
I am currently conducting research on topological optimization, exploring topological regularization in Nonnegative Matrix Factorization (NMF). NMF is one of the linear dimensionality reduction methods used to extract latent features (basis vectors) from a dataset. However, standard NMF does not explicitly capture the structural or topological properties of the data. My research focuses on applying topological regularization to NMF to extract latent features that preserve topological characteristics, such as connectivity and the presence of holes. The goal is to obtain more interpretable latent features from the dataset, enhancing the structural understanding of the extracted components.

