I study (1) integrable systems and related geometry and (2) applied physics, with a focus on elliptic theta functions. Elliptic theta functions are known for their rich mathematical properties and appear in a wide range of mathematical fields. In the case of my research, these properties are used to construct exact solutions to integrable systems. They are also important for discretizing equations from the information contained in the solutions and for discovering nontrivial conserved quantities. Below are some examples of applications of theta functions with specific examples.

(1) Integrable systems and related geometry:

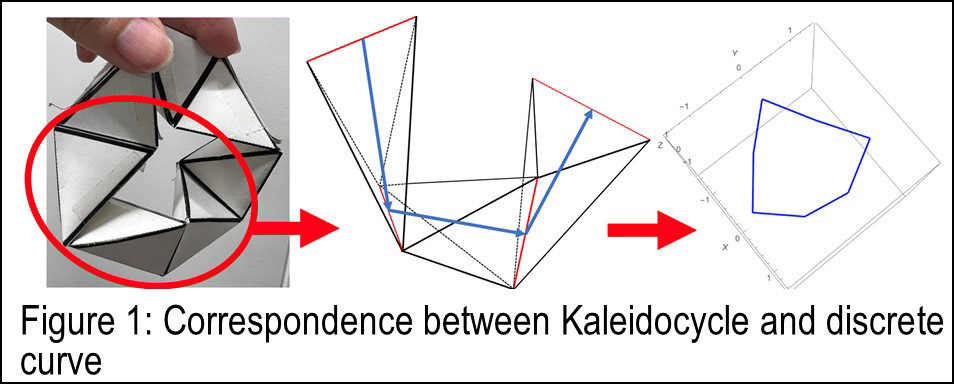
　Integrable systems are a family of differential equations whose exact solutions can be constructed using well-known functions, despite their nonlinearity. There are various applications of integrable systems, but an example is the Möbius Kaleidocycle. This is a linkage mechanism consisting of six or more congruent tetrahedra connected by hinges to form a ring. This mechanism is interesting from a mathematical, physical, and engineering point of view because it has a single degree of freedom of motion, but it is usually challenging to perform a rigorous analysis of a linkage mechanism. However, if this mechanism is viewed as a discrete curve with constant torsion (Fig. 1), the deformation can be described by an integrable system, and not only the torsion and curvature of the curve, but also the position vector can be constructed explicitly using theta functions. This result has led to the discovery of previously unknown conserved quantities, etc., and is expected to play an important role in the future analysis of Möbius Kaleidocycle.

(2) Applied physics:

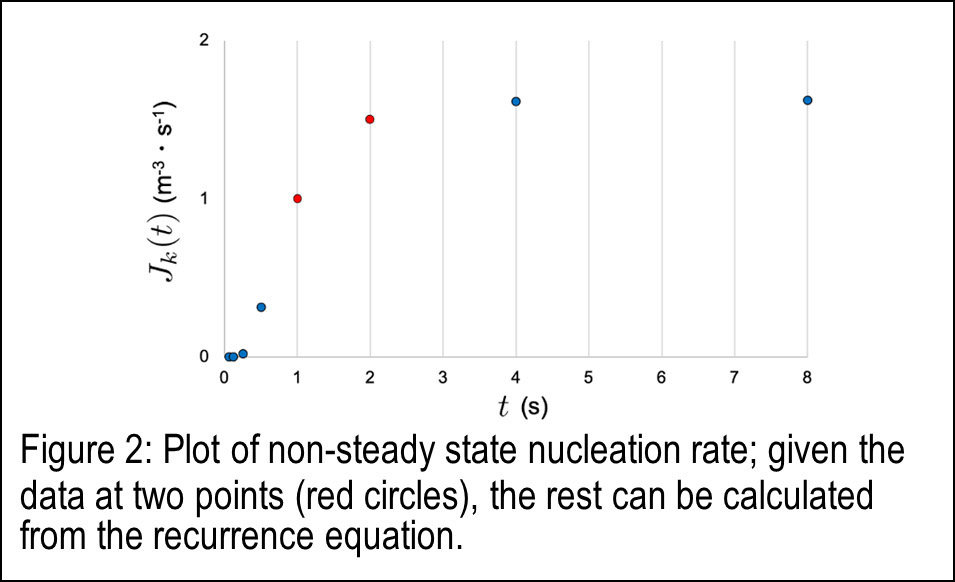
　Theta functions also appear in physics, and I have been using them to study phenomena in applied physics. Non-steady state nucleation is a phenomenon such as that seen in the initial stage of vesiculation of carbonate water, which can be observed in daily life. This phenomenon is characterized by a quantity called the non-steady state nucleation rate J_k( t ). Measuring this quantity may require a long experiment, which presents a cost challenge. On the other hand, it was pointed out in 1969 that J_k( t ) is expressed by an elliptic theta function, but since its publication, there were no research utilizing the properties of theta function. In this study, nontrivial recurrence equations satisfied by J_k( 2ⁿt ) were derived using the properties of theta functions, allowing the value of J_k( t ) to be estimated with a small amount of data (Fig. 2). The results can be used to reduce costs in experimental studies of non-steady state nucleation.