I mainly study the parabolic partial differential equations (PDEs), where “parabolic” means one of the classifications for the PDEs and the typical example might be the heat equation.

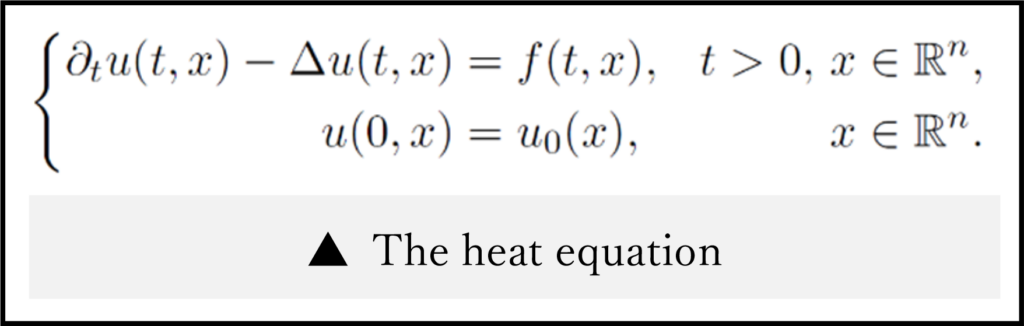
For instance, when a frying pan is heated, the transition of its temperature is dominated by the heat equation: Of course, phenomena in the real world should depend on numerous external factors. However, in ideal situations, various physical phenomena are expressed via differential equations. Indeed, the parabolic PDEs may describe physical phenomena other than the heat equation. Such examples are the Navier–Stokes system, which is the equation of motion for the incompressible viscous fluid (e.g., water), and the Keller–Segel system, which is a mathematical model describing a cell-moving phenomenon via the reaction of certain chemical stuff (chemotaxis).

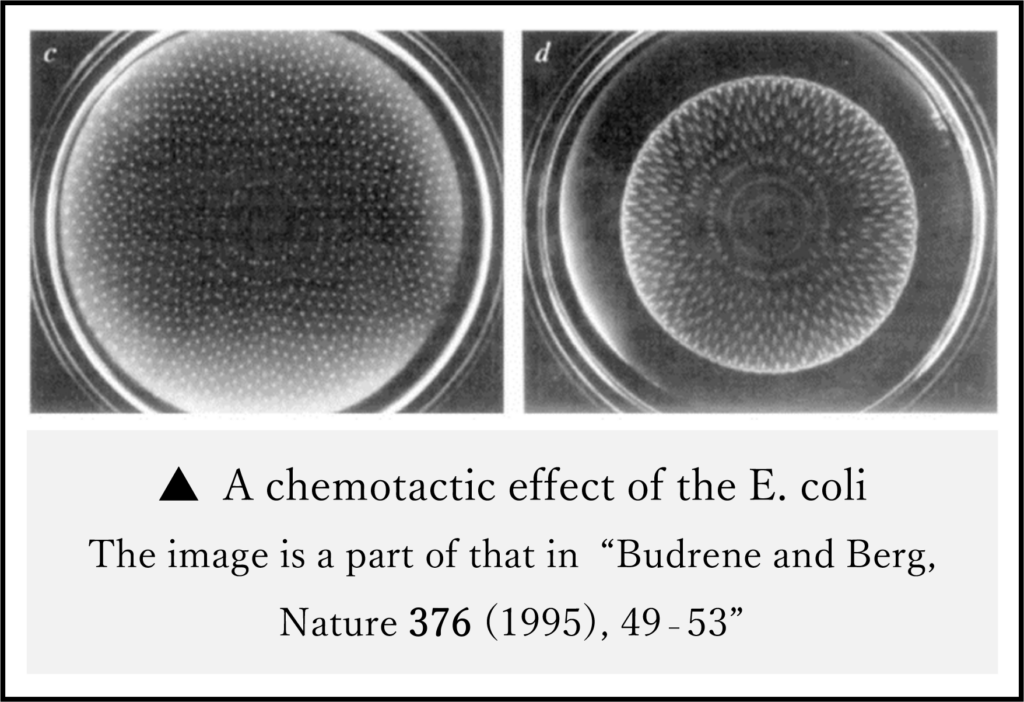
The Navier–Stokes system is the foundation of fluid dynamics and supports various applied fields in the real world. In addition, the Keller–Segel system is applied to the phenomena of cancer metastasis and Alzheimer’s disease, and hence it plays a crucial role in the development of medical technology. In this way, the mathematical analysis of the (parabolic) PDEs is closely related to various issues in the real world.
Let us consider how to analyze the parabolic PDEs: The most fundamental question from the viewpoint of the differential equation theory might be “whether solutions exist or not”. If the differential equation describes a physical phenomenon exactly, then such a phenomenon should be forecast by relying only on numerical simulations without any theoretical analysis. However, it is unclear whether such an equation expresses the corresponding phenomenon exactly; there is a possibility that the equation does not have a solution in the mathematical sense. We thus need to find exact solutions, which is one of the motivations of the mathematical analysis. In particular, as for me, I would like to extend the mathematical conditions ensuring the existence of solutions.
Here let us introduce the keyword “Harmonic analysis”: There are several ways to investigate differential equations mathematically. In particular, I rely on the method that is based on the harmonic analysis. Many people have heard of the word “Fourier transform” somewhere; harmonic analysis means the analysis using the Fourier transform.

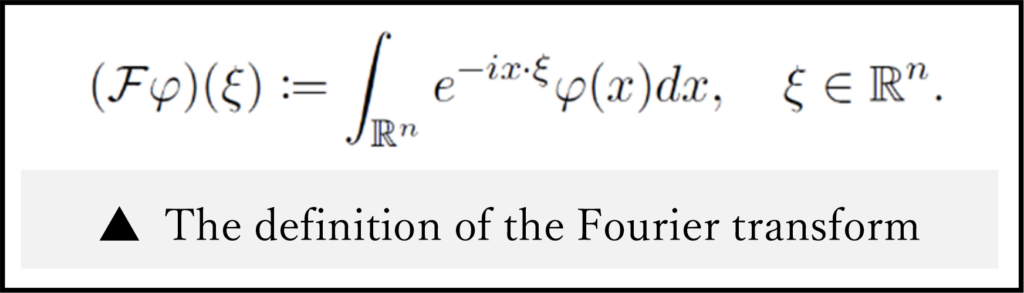
Introducing suitable function spaces would be necessary for the mathematical analysis of differential equations; the function spaces based on the harmonic analysis are a strong tool in my research method. In particular, the useful point is that the smoothness of functions is expressed by the increasing rate corresponding to the functions’ frequency, unlike differentiability.
There have been numerous works on the (parabolic) PDEs via harmonic analysis: While various results have been obtained, further developments are also expected in this direction. I hope that my work will help such developments even a little.