My primary research interest lies in the intersection of Topological Data Analysis (TDA) and Machine Learning (ML). In particular, I am currently focused on optimization problems in TDA.

Topology is the study of continuous objects, known as topological spaces, and the properties that remain invariant under continuous deformation. One of the most well-known invariants is homology, which quantifies the “holes” in a space and can be efficiently computed using linear algebra.

TDA can be applied to various types of data, including point clouds, time series, and images. Persistent homology is a central tool in TDA, which quantifies the connectedness, holes, and higher-dimensional structures present in the data. These topological features are summarized using a persistence barcode.

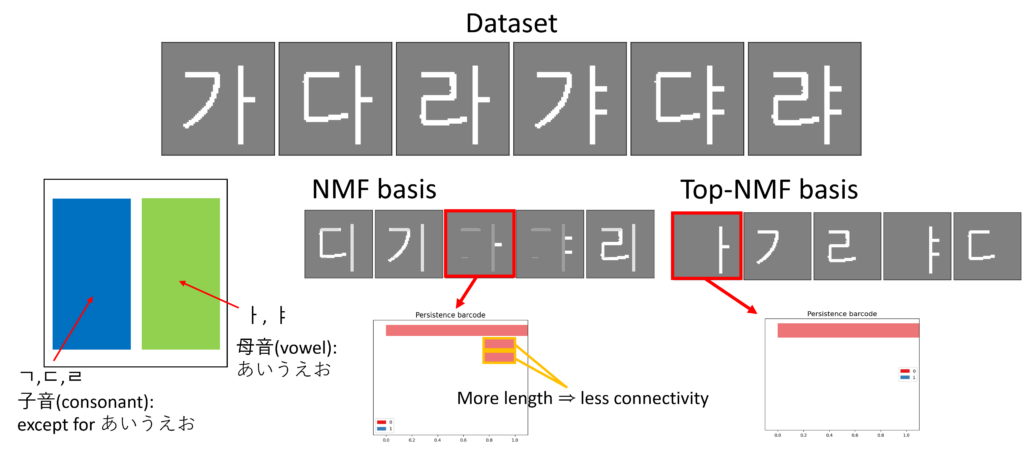
Figure 1 illustrates the core idea of this study in an intuitive manner using a Hangul image dataset. The characters shown in the figure—namely 가, 다, 라, 갸, 댜, 랴—are structurally composed of basic elements, namely consonants (ㄱ, ㄷ, ㄹ) and vowels (ㅏ, ㅑ). While humans naturally perceive these consonants and vowels as meaningful and fundamental decomposition units, applying a purely data-driven matrix factorization method, such as standard Nonnegative Matrix Factorization (NMF), often leads to undesirable results. In particular, the basis vectors learned by NMF may exhibit disconnected strokes, resulting in characters being represented as fragmented or semantically meaningless pieces. As shown in the red boxes in the NMF basis row of Figure 1, a single character appears as three mutually disconnected components. This structural fragmentation is directly reflected in the persistence barcode shown at the bottom of the figure. The short bars correspond to disconnected components, and their lengths can provide a quantifier of the degree of disconnectedness in the extracted basis. This example highlights how topological information can be used to characterize and quantify structural deficiencies in standard NMF, thereby motivating the introduction of topological regularization.

I am currently conducting research on optimization problems in TDA, with a particular focus on incorporating topological regularization the NMF (Top-NMF). By encouraging the decomposed components to exhibit topological properties such as connectivity and hole structures, we aim to derive semantically interpretable fundamental decomposition units.

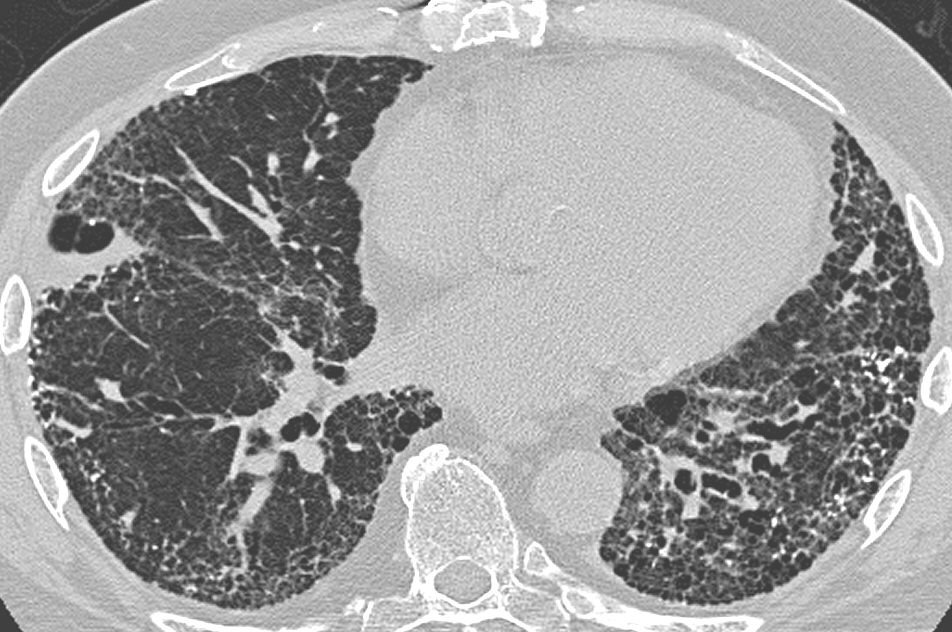
In addition, as a researcher participating in Moonshot Project 2, which focuses on ultra-early disease diagnosis, I am applying my theoretical framework to the analysis of medical imaging data. For example, certain lung diseases, such as honeycomb lung, exhibit characteristic topological structures in which holes appear within lung tissue, and, as illustrated in Figure 2. Building on the theoretical framework presented in Figure 1, future research aims to capture fundamental patterns observed in patients with lung diseases and to explore how this information can be utilized to support lung disease diagnosis.