ソリトンと呼ばれる，粒子性をあわせ持つ非線形波動の研究に端を発する「可積分系」の研究を軸に研究活動を行っています．数理的には，ソリトンを記述する基礎方程式（ソリトン方程式）は非線形偏微分方程式であるにもかかわらず厳密に解けるという，奇跡的な性質を持っています．その奇跡の背後には「無限自由度の対称性をもつ無限次元の空間」の数理があり，その数理を共有する函数方程式の族を「可積分系」と呼びます．背後の数理を深く理解することによって，可積分系は多くの分野への応用が可能です．以下，私が関わっている３つの例を挙げます．

1. 離散化と超離散化：ソリトン方程式の可積分性を保存したまま独立変数を離散化して差分方程式を構成したり，従属変数まで離散化してセルオートマトンを構成する方法（「超離散化」）が構築されています．図１上は典型的なソリトンの相互作用を表し，左からやってきた大きく速いソリトンが小さく遅いソリトンを追い抜いています．一方，図１下はソリトンを記述するセルオートマトンです．１次元の箱の列と玉があるとし，各時刻で左から玉を右の最も近い空箱に移し，全ての玉を移動したら時刻を１進めます．この単純なモデルがソリトンを記述し，超離散化の手続きで偏微分方程式と直接の対応がつきます．離散化・超離散化の理論は数値解析や交通流など広範な分野に応用され，大きな成功を収めており，私が展開する他分野，特に幾何に関係する分野との連携活動のバックボーンを成しています（離散微分幾何）．最近では超離散化の適用範囲が可積分ではない反応拡散系にも拡大され，性質のよい反応拡散セルオートマトンモデルが構成できるようになっています．さらに，超離散系の背後の構造が最近急速に発達している「トロピカル幾何学」でよく記述されることが判明し，純粋数学の発達も促しています．

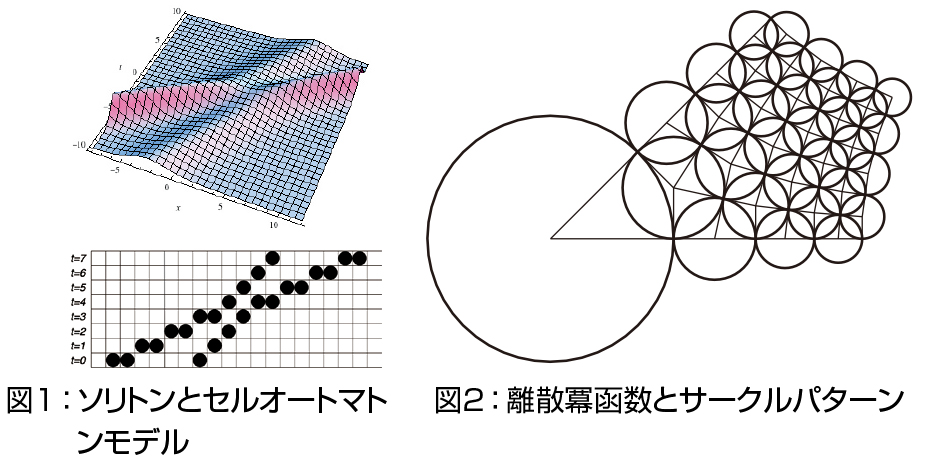
2. 離散パンルヴェ方程式と楕円曲線：離散パンルヴェ方程式と呼ばれる可積分な２階常差分方程式の族は，数理物理学や特殊函数論で重要な役割を果たし，背後に極めて豊富な構造があります．その解はよく知られたベッセル函数や超幾何函数などの特殊函数の一般化と見なすことができます．これらの頂上にE_８^(１)型の対称性を持つ「楕円パンルヴェ方程式」があり，特殊解として楕円テータ函数で表示される「楕円超幾何函数」が現れます．この函数は超幾何型特殊函数の頂上に位置するものと考えられています． 離散微分幾何における応用の一つとして，ある種の複素正則函数の離散化をパンルヴェ・離散パンルヴェ方程式が記述します．図２は冪函数Z^１/２の離散化で，グリッドはサークルパターンで特徴付けられます．

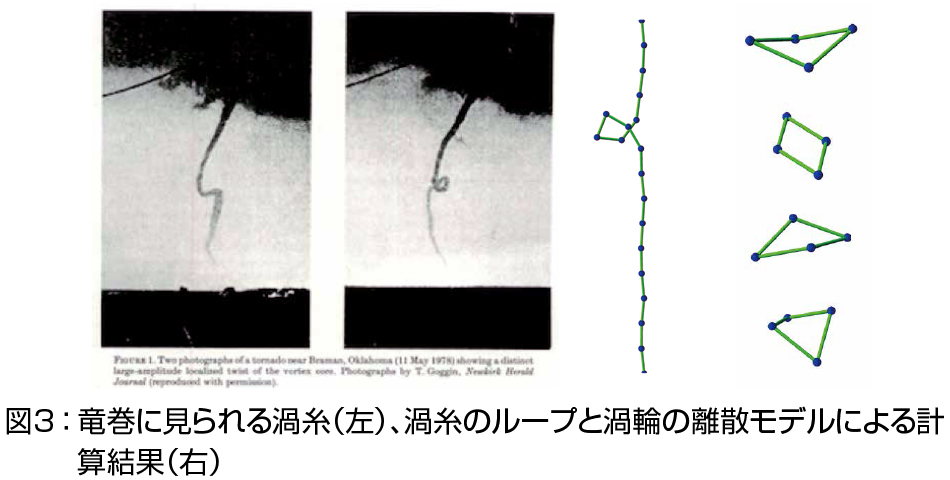
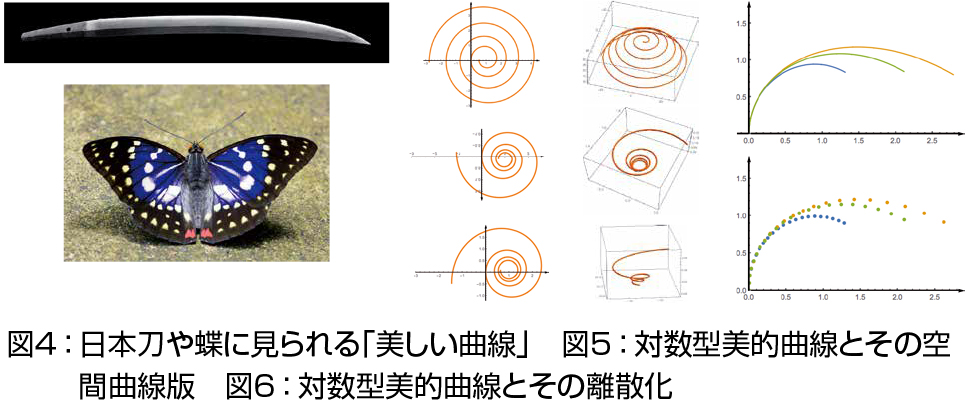
3. 離散可積分微分幾何と幾何学的形状生成：空間中の曲線・曲面やその変形を記述する基礎方程式としてさまざまな可積分系が現れることが知られています．さらに最近，離散可積分系と整合する曲線・曲面論の構築が進み，私は幾何学的形状生成，特に何らかの意味で「よい」曲線・曲面の生成の研究を工業意匠設計や建築の専門家と協力して進めています．図３は天然の渦糸である竜巻と，その離散モデルの計算結果．背後の構造を保存しているので，コストの低い計算で高品質な結果が得られます．図５（左）は工業意匠設計において，美的要素をもつ形状要素として日本で提唱された「対数型美的曲線」と呼ばれる平面曲線の族で，日本刀や蝶の羽など，私たちが「美しい」と思う形状から抽出されました（図４）．最近，私たちは可積分幾何の立場から全く新しい理論的枠組みを提唱し，それを用いて構造を保存した，高速生成可能で高品質な離散化や（図６），空間曲線への一般化を構築しました（図５（右））．この理論を曲面に拡張し，得られた美的要素をもつ曲線・曲面の族を幾何学的形状要素として実装し，意匠設計での標準化を目指して研究を進めます．これらの形状は「美しさ」という人間の感覚の要素を取り込んだ数理モデルとしても重要な例です：よい方程式は，よい形状を生成する．